(1)飽和(クリップ)による歪み
増幅器の出力振幅が0Vから電源電圧までしか振れない^※2ことに起因する歪みです。直感的に理解やすく、多くの方が「増幅器の歪み」というとこの現象を想像されることと思います。

トランジスタ増幅器では色々な特性表現で「飽和」という言葉を多用しますが、ここでいう「飽和」とは入力電力 対 出力電力特性の飽和を示し、入力電力をいくら大きくしても出力電力が大きくならない状態を示します。図1の右上にイメージを示したとおり、増幅器の入力が過入力状態になって出力が飽和すると出力波形がクリップされて矩形状の波形に変形します。サイン波のような周期関数の信号がクリップされると、波形には周期関数のn乗(n=2,3,4･･･)、特に矩形になった場合は奇数乗のスペクトル成分が付加されます。

• ※2  厳密には、「電源電圧で決まる最大振幅」になります。例えば高周波増幅器で一般的なL負荷の増幅器では、出力振幅はコレクタ電圧V_CCを基準に振れるため、
  最大振幅は0[V]～2×V_CC[V]となります。

(2)大振幅動作による歪み
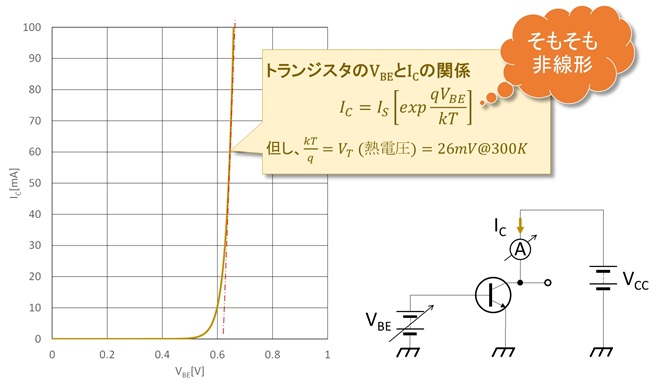
この歪みは増幅器の入出力特性が本質的に指数関数であることに起因する歪みです。我々は通常トランジスタ増幅器の入出力特性を「線形」と見なしがちですが、「今更聞けない無線と回路設計の話【テーマ1】三角関数のかけ算と無線工学 第2話 周波数変換とミキサ(混合)回路」で少し解説したとおり、半導体のpn接合部を流れる電流は接合部電圧の指数関数になる(図3)ため、トランジスタを用いた増幅器の入出力特性も本質的に指数関数になります(図4)。

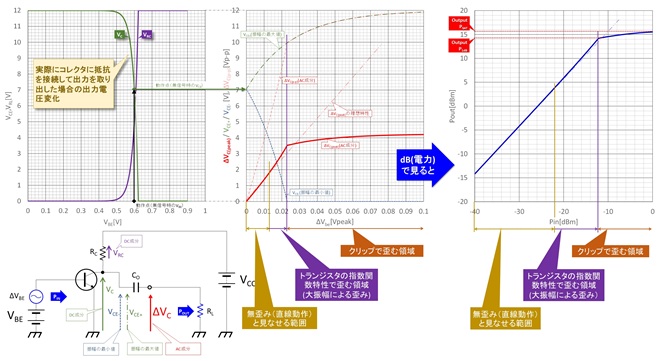
図4の左のグラフは図3の特性から、トランジスタのコレクタに負荷抵抗R_Cを接続し、V_CC=12Vで動作させたときのコレクタ電圧変化(すなわちV_BE対V_CE特性)を示したもの。中央のグラフは左のグラフで定めた動作点(V_BE=0.6V→V_CE=7V)で、この回路の入力にAC振幅を与えた時のコレクタ電圧の振幅ΔV_Cを計算したものです。V_BEの振幅(ΔV_be)を大きくすると、コレクタ電圧はグラフのV_CE+とV_CE-の間で振れる事になります。この回路の理論上の最大出力振幅: 12V_P-P=6V_peakに対して、入出力直線性が確保できるのは、せいぜい2V_peak程度であることが読み取れると思います。右側の直線目盛のグラフで読むととても悪い性能に見えますが、普段見慣れている対数(デシベル)のグラフで見ると、P_SAT－12dB弱という感じです。

図3 トランジスタのV_BE vs I_C特性

図4 トランジスタの線形領域と非線形(歪みが発生する)領域

これほど非線形の増幅器をなぜ「線形」と見なす事が出来るかというと、通常はオペアンプのように負帰還をかけて補正したり、「小信号動作」と言って、指数関数≒線形と見なせる狭い振幅領域でトランジスタを使用しているからです。小信号増幅回路という増幅回路が如何に小さな信号を取り扱っているかがおわかりいただけると思います。

図3に示したように、トランジスタのベース・エミッタ間電圧V_BEとコレクタ電流I_Cの間には以下の関係があります。

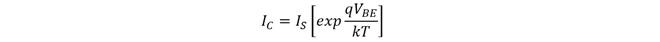
(式2-1)

但し、I_S は逆方向飽和電流(デバイス依存の定数)、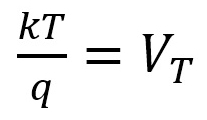(熱電圧) = 26mV@300Kなので、

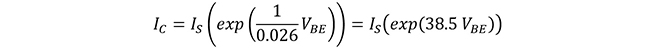
(式2-2)

指数関数は級数に展開することが可能で、マクローリン展開すると

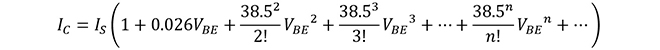
(式2-3)

となります。従ってこのような特性をもつトランジスタで信号を増幅すると、出力には入力信号のn乗(n=1,2,3･･･)の成分が含まれる事になります。級数のn乗成分を、n次成分と呼びます。一般に伝送信号は複数の周波数スペクトルから構成されるので、ここでは複数のサイン波の合成信号がn乗されるとどうなるかを考える必要があります。話を簡単にするために入力信号を cos ω₁t  + cos ω₂ として、 これを2乗、3乗するとどのようなスペクトルが出現するかを考察します。まず2次の項は、

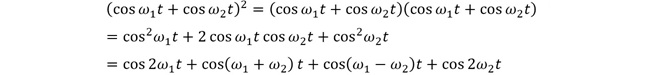
(式2-4)

となって、元のスペクトルが2逓倍された成分と、相互にかけ算された成分が現れます。これは「今更聞けない無線と回路設計の話【テーマ1】三角関数のかけ算と無線工学」の第2話「周波数変換とミキサ(混合)回路」で解説した非線形回路を用いた乗算動作の原理式です。

続いて3次の項は、

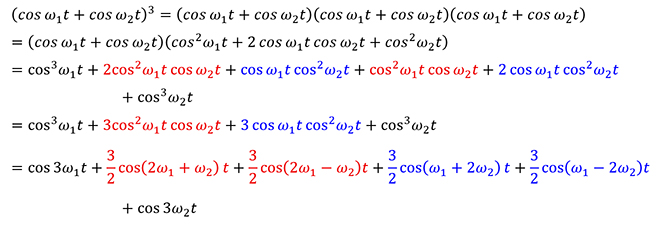
(式2-5)

となって、元のスペクトルが3逓倍された成分と、片方が2逓倍された成分に他方をかけ算した成分(赤字: cos ω₁t の2逓倍にcos ω₂ をかけ算した成分、青字: cos ω₂t の2逓倍にcos ω₁ をかけ算した成分)が現れます。この様子を図5に示します。

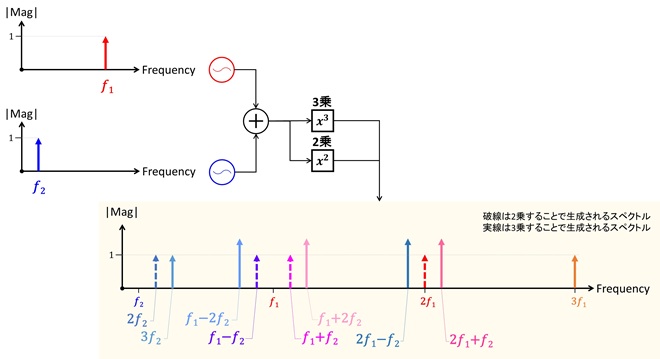
図5 𝑓₁+𝑓₂信号を2乗、3乗したときに生成されるスペクトル

3. 第11話のまとめ

このようにトランジスタ増幅器の伝達関数は指数関数なので、大振幅の信号を取り扱うと入力信号のn乗成分が多数生成されます。図5だけを見ていると、何れも入力の信号スペクトルと重ならないので、信号劣化に寄与しないように見えますが、入力のスペクトルの近くに生成される𝑓₁+2𝑓₂と𝑓₁−2𝑓₂は、三次歪み成分として伝送信号の劣化に大きく寄与します。次回はこのあたりを中心に解説したいと考えます。以下、第11話の要点です。

• (1)位相回転量と遅延量が異なる自信号の合成で生じる線形歪みはスペクトル構成に変化が生じないが、信号が伝搬路の非線形性で変形する非線形歪みは、自信号以外にあらたなスペクトルが発生する。
• (2)トランジスタ増幅器(FETも同じ)の伝達関数は指数関数であるため、負帰還回路などを併用しない限り、大振幅の信号を扱うと必ず歪みが発生する。
• (3)増幅回路の出力振幅には電源電圧で制約された上限振幅があり、出力振幅がこれに達すると、入力振幅をそれ以上大きくしても、出力振幅はおおきくならない。(飽和)
• (4)増幅器の出力飽和レベルを示すパラメータとして、飽和出力電力P_SAT、利得1dB抑圧出力電力P_1dBが良く用いられる。
• (5)増幅器が飽和することによりクリップされた信号には、指数関数の伝達関数の影響と同様、元の信号のn乗の成分が発生する。

第12話では引き続き三次歪みが伝送信号にどのように影響するかを解説します。