第25話では、マイナスの周波数と交流ベクトル空間について解説しました。第26話も引き続き交流ベクトルとサイン波の関係について解説します。

1. 同時に観測できない虚数軸

少しだけ第25話のおさらいです。図1は第25話の図5を少し整理したものです。交流ベクトル空間において、交流電圧(または電流: 以下、電圧で記載します)は大きさV_m、早さω(=2πf )で回転する二次元のベクトル量でした。ベクトルが回転している状態では取り扱いが不便なので、実際に取り扱うときは時刻t=0[sec]の瞬間を切り取って使用します。t=0で切り取った交流ベクトル空間に表示される交流電圧は大きさV_m、初期角度(位相)φ のベクトルとなります。

図1 交流ベクトル空間

オシロスコープで観測される波形は、図1に示した交流ベクトル空間のどこかの側面から見た電圧ベクトルと言うことになります。オシロスコープのトリガ電圧を何[V]に設定するかによって、観測する側面が交流ベクトル空間の周りを回転します。つまり観測している側面(これを実軸とする)と直交した方向から観測したときの電圧変化(虚軸方向の電圧変化の投影)を同時に見ることはできません。この事にどのような意味があるのか･･･、気になりますが第26話ではとりあえず、直交した方向から観測したときの電圧変化をどうすれば同時に見ることができるか、について先にお話しします。結論から言うと「直交検波」という特殊な周波数変換を行うことで、実軸の瞬時値と虚軸の瞬時値を分離して観測することが可能です。

2. 直交ミキサ

直交検波を行うには直交ミキサと呼ばれる周波数変換回路を用います。これは図2に示すように同じRF信号を90°の位相差をつけたLO信号･･･ すなわちコサイン波とサイン波でおのおの周波数変換するものです。判ってしまえば「なんだそれだけ?」って感じかもしれません。

図2 直交ミキサ

LO信号はコサイン波(と定義した方)を基準として90°位相が遅れている方をサイン波と定義します。識別のため、コサイン波と乗算した出力をI、サイン波と乗算した出力をQと名付けます。また話を簡単にするためにミキサは理想的な乗算回路と仮定します。位相の概念がなかった第24話までの周波数変換の解説に従えば、ミキサの入出力関係を示したグラフA～Dに示すように、I出力(グラフC)もQ出力(グラフD)も同じグラフになります。ではI出力とQ出力で何が変わるのかと言うと、吹き出し②③に示すように和周波(USB)、差周波(LSB)各スペクトルの位相が異なることになります。図2の吹き出しに書かれている計算式は第1話の2章で示した三角関数の加法定理のバリエーションで、コサイン側が(式2-7)、サイン側が(式2-6)になります。両者の違いをベクトルで表記したのが図2の出力側の吹き出し②と③です。Q出力はI出力を基準にしてUSB(和周波)側が90°遅れ、LSB(差周波)側が90°進みとなります。ここでも結論から言いますが、このときI出力(USB①とLSB①の組み合わせ)が実軸の観測波形、Q出力(USB②とLSB②の組み合わせ)が虚軸の観測波形を示すことになります。

つまり乗算するLO信号の位相を変化させることで、周波数変換された結果が実軸成分だったり虚軸成分だったりすると言うことなのですが、ちょっとイメージがつかみにくいと思うので、視点を変えた解説をしたいと思います。

3. 周波数変換とサンプリングの切っても切れない関係

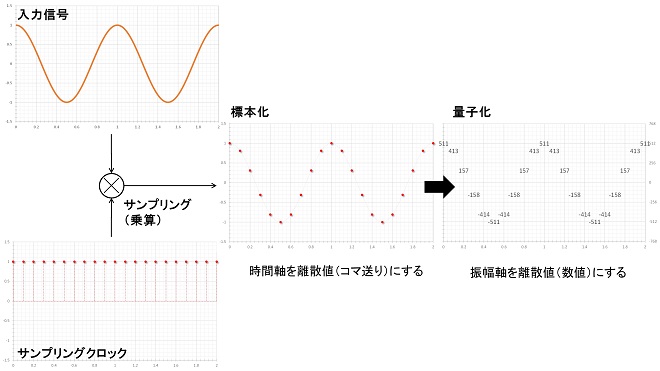
話が少し飛びますが、映写機の動作やADコンバータの動作を語るとき、「サンプリング(標本化)」という概念が登場します。我々は連続する事象を記録する際、連続したままで媒体に記録することができない^※1ため、連続する事象をいわゆる「コマ送り」状態に切り取って記録します。これを一般化すると図3のようになります。サンプリングとは、時間軸上で連続した事象を一定間隔毎に切り取った値の数列にする操作で、映写機ならシャッターの開閉、ADコンバータなら入力信号に対してサンプリングクロックという一定の周波数で1→0を繰り返す信号を乗算することで実現しています。

図3 ADコンバータによるデジタイズの概念

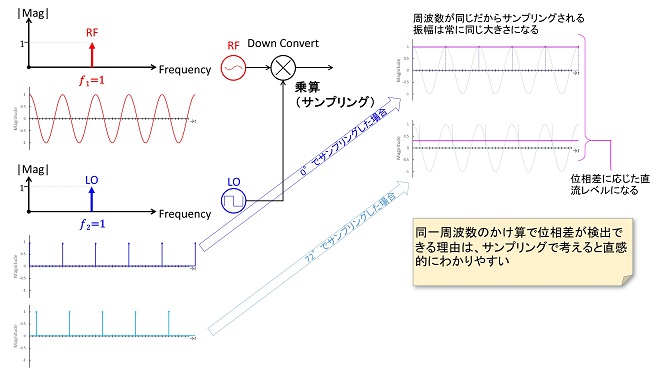
デジタル化したい信号(RF信号)にサンプリングクロック(LO信号)を乗算して標本化(周波数変換)するという処理は実は周波数変換と同じ処理になります。従って周波数変換の時間軸上での動作イメージはRF信号をLO信号でサンプリングしていると考えれば直感的に理解しやすくなります。まず第12話で解説した「同一周波数のサイン波をかけ算」したときの話です。同一周波数のサイン波をかけ算すると、両者の位相差を示す直流電圧と二倍の周波数の信号が得られるというのが第12話の結論でした。これをRF信号を同一周波数のLO信号でサンプリングしているという考え方で解説したのが図4です。

図4 サンプリングの概念で解説した同一周波数同士のかけ算

図4においてLOはサンプリングクロックなので、サイン波ではなく一定周期で1のインパルスを繰り返す信号になります(図のLOシンボルに書かれているようなデューティ比50%の矩形波ではありません。)。LOとRFの周波数が同じなのでRFをLOでサンプリング、すなわちLO=1の瞬間の値のみ拾ってプロットすると、常に同じ値が得られることになります。LOの位相を変化させると、RF信号をサンプリングするポイントが変化するので、出力の電圧値が位相差に応じて変化することになります。第12話では三角関数の加法定理から位相が検波できることを解説しましたが、実はこちらの方が直感的にわかりやすいのではないかと思います。

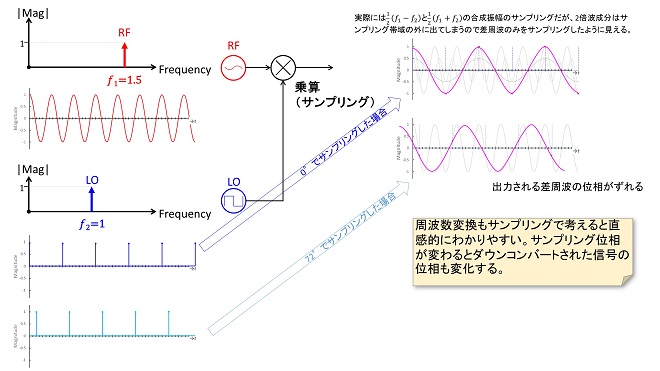
次にRFとLOの周波数が異なるケースを図5に示します。

図5 サンプリングの概念で解説した異なる周波数同士のかけ算

RFとLOの周波数が異なる場合も、RFをLOでサンプリングすると、差周波の成分が現れる様子とRFとLOの位相差が出力位相に反映される様子が直感的に理解できるのではないかと思います。

4. サンプリング位相と交流ベクトル空間の関係

図5の関係と図１の交流ベクトル空間を対応づけたのが図6です。図5に示したLO(サンプリングクロック)に位相72°の位相回転を与えると言うことは、図6に示すように交流ベクトル空間(平面)の72°の軸に投影される電圧振幅をサンプリングするという操作を行ったのと等価になります。このとき、周波数変換された出力信号(LSB)の位相は図からわかるように、RFとLOの位相差が保存されます。入力側の位相差に相当する遅延時間差が出力現れるのではなく、変換された周波数の位相として反映されることがポイントです。図5では差周波成分(LSB)しか読み取れませんが、実際には(式4-2)に示す通り、出力のLSB成分(差周波)にはRFの絶対位相φ_RF とLOの絶対位相φ_LO の差、USB成分(和周波)にはRFの絶対位相φ_RF とLOの絶対位相φ_LO の和が反映されます^※2。

　・三角関数の加法定理(第1話の(式2-7))

(式4-1)

　・(式4-1)にRF信号の周波数ω_RF + φ_RF , LO信号の周波数ω_LO + φ_LO を代入

(式4-2)

図6 サンプリングクロックの位相と交流ベクトル空間の関係(1)

これらの結果から、虚軸に投影された波形を見るためには、図7に示すとおり、サンプリングクロックの位相を90°までずらしてやればよいと言うことがわかります。これによって周波数は変換されてしまいますが、虚軸に投影された波形を見ることが可能になります。

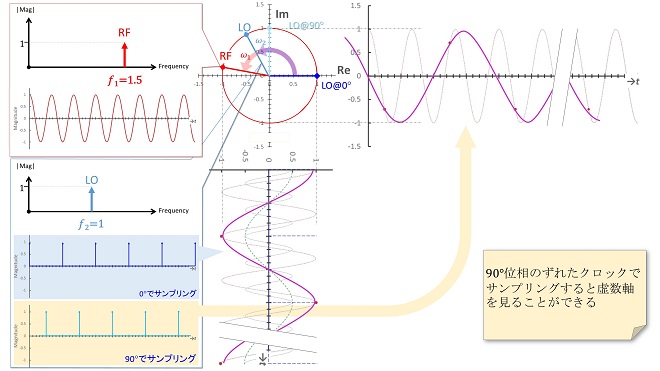
図7 サンプリングクロックの位相と交流ベクトル空間の関係(2)

これをインパルス信号ではなくサイン波で行っているのが図2に示した直交ミキサです。図2において、直交ミキサのI出力を基準に置くと、サイン波とかけ算したQ出力はI出力と直交した成分が出力されると言うことになるのです。

5. 第26話のまとめ

第26話では、直交ミキサの構成と動作原理に触れ、周波数変換したときの出力信号の位相が入力信号の位相でどのように変化するかについて、サンプリングの概念を用いて解説しました。

以下、第26話の要点です。

• (1) 交流ベクトル空間の実軸と虚数軸は直交ミキサで周波数変換することで別々の信号として観測することができる。
• (2) 周波数変換(入力信号にLO信号を乗算)と、サンプリング回路(入力信号にサンプリングクロック(インパルス信号)を乗算)は、本質的に同じ動作である。
• (3) 周波数変換出力の位相は、差周波(LSB)側が入力信号の位相差、和周波(USB)側が入力信号の位相和になる^※2。差周波(LSB)については入力(RF)信号をLO信号でサンプリングすると考えると直感的に理解しやすい。

今回は交流ベクトルの直交が何を意味するのかを全く解説していないので、「だから何なの?」という感想をお持ちの方もおられると思います。第27話では交流ベクトルの直交の意味について解説したいと考えます。

• ※1 アナログレコード、アナログテープレコーダにはコマ送り(サンプリング)の概念がなく、媒体に連続的に記録しています。
• ※2 RF信号とLO信号は周波数が異なるので両者の位相差は通常定義できません。(式4-2)が示すRF信号の絶対位相φ_RF 、 LO信号の絶対位相φ_LO とは、ある基準時刻(t=0)における、それぞれの信号の初期位相の値であり、位相差とはそれらの差、位相和とはそれらの和を示しています。