今更聞けない無線と回路設計の話
【テーマ2】デシベルと無線工学
第3話 dB(デシベル)を知る(その2)
2024年12月2日掲載
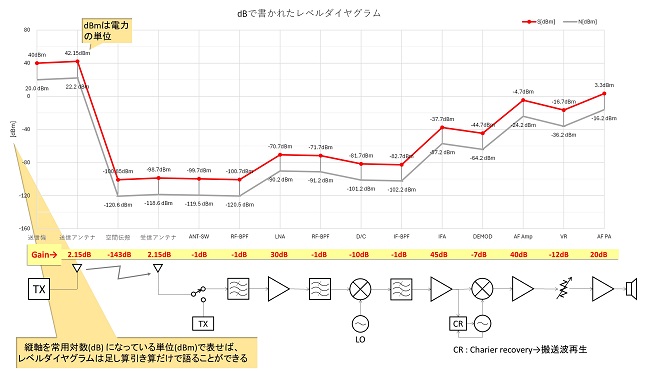
第2話では、dB(デシベル)の定義と「何故レベルダイヤグラムを扱うときはdB(デシベル)を用いるのか」について解説しました。1[dB]とは0.1[B]のことで、B(ベル)とは利得、すなわち比率の常用対数に用いる単位でした。これとは別に第2話で登場したレベルダイヤグラム(図4)の縦軸の単位はdBではなくdBmでした。世の中にはこのようなdB○×(“○×”には1~数文字のアルファベットが当てはまる)という単位がたくさん存在します。第3話では、このdB○×について解説します。
1. dB○×(デービー○×)が必要なわけ
既に第2話で結論を書いているのですが、回路ブロックの利得をdB(デシベル)で表して、縦軸の単位を[W]のままでレベルダイヤグラムを作成しようとすると、図1に示すように縦軸は対数目盛となり、1枚のグラフにはなれども都度「対数-真数変換」の計算が必要になって、作成するのも値を読むのも不便です。
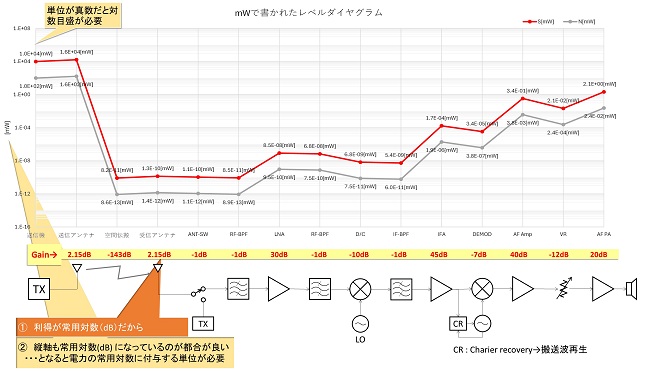
図1 縦軸をW(mW)で表記して対数目盛で作成したレベルダイヤグラム
従って、信号のレベル(グラフの縦軸)も利得と同様に常用対数の単位で表現できることが望ましいのですが、一般に常用対数の電力や常用対数の電圧の単位というものは存在しません。そこで1倍を表す0dB(デシベル)に電力(W)や電圧(V)などの物理量の基準値を対応させて“dB”を常用対数の絶対量の単位として利用するという手法がとられます。これが“dB○×”(デービー○×)と呼ばれる“dB”達です。このような使い方をする“dB”は、同じ“dB”でも“デシベル”とは読まず“デービー”と読みます。こちらはB(ベル)と違い、“dB”ひと塊で常用対数であることを示す一種の補助単位? と解釈することができます(国際単位系にそのような規定は存在しないので、あくまで慣用的な解釈です)。図1のレベルダイヤグラムでは縦軸は電力、単位はmWでした。mWに対応する常用対数の単位は、1mW=0dBと紐付けしたdBm(デービーエム)という単位です。縦軸をdBmで表現したレベルダイヤグラムは図2に示す通り、縦軸が等間隔目盛りとなって読み取りやすいグラフになります。
2. dB○×(デービー○×)の仲間達
では、常用対数値の単位としてよく使われるdB○×には、どのようなものがあるでしょうか。無線屋さんの観点で表1に整理してみました。

表1 無線屋がよく使用するdB○× (絶対量を表すもの)
このうち、最も頻繁に使用されるのが電力の単位であるdBmと電圧の単位であるdBµ(またはdBµV)でしょう。dBmは1mWを基準(=0dB)とした電力の常用対数単位、dBµとdBµVは同意で1µVを基準(0dB)とした電圧の常用対数単位です。昨今の文献では電圧を示す単位については必ずVをつける傾向があります。これら2つの単位については、第4話でも詳しく掘り下げようと思います。
音響機器では音の大きさを示すのに音圧(空気圧)を使用します。dBSPLのSPLは音圧: Sonud Pressure Levelを示しており、人間の低圧側可聴限界(つまり最も小さい音)といわれる20µPa(マイクロパスカル、気圧の単位がbar(バール)だった頃の0.0002µbar(マイクロバール)に相当)を基準(=0dB)とした音圧の常用対数単位です。
dBFSはアナログ信号をDAコンバータで量子化した際の振幅を対数表現するときに使用する単位で、フルスケール(あと1digit増える(減る)とオーバフロー(アンダーフロー)する値)を0dBとした単位です。
3. dB○×(デービー○×)の注意点
これらの単位は絶対量を示すものであって、dB本来の用途である「比」は示していません。従って複数諸元間の比を扱う時には注意が必要です。
例えばA局の送信機の出力は+30dBm(=1W)でB局は+33dBm(=2W)の時、
B局はA局よりも送信電力が「3dBm(=2mW)大きい」と言う表現は間違いで、
B局はA局よりも送信電力が「3dB大きい」(送信電力が2倍である)が正解です。
またベテラン同士の会話でも良く混同されるのですが、
「B局とA局の送信電力差は3dB」という表現がなされることがよくあります。厳密には
「B局とA局の送信電力比は3dB」というのが正しい捉え方です。
常にdBを使用していると、比を語っている感覚が薄れてしまい、ついつい「差」と表現しがちです。それが対数を使用する目的でもあるので、あながち間違いではないですが、現実を捉えているつもりで現実離れな事を考えてしまう原因になるので注意すべきでしょう。
4. dB○×(デービー○×)のようでいて絶対量を示さないdB○×
無線屋さんがよく使うdB○×で絶対量を示さないものがあります。これらは主に変換利得等、比例関係にあって形態の異なる2つのエネルギーの比を示す目的で使用される単位です。これらを表2にまとめます。
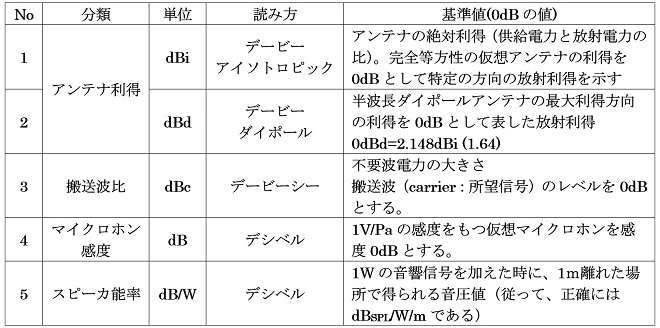
表2 絶対量を表さないdB○×
このうちNo3のdBcは同種の異なる信号のレベル比ですが、その他の単位が示すのは、変換利得、すなわち形態の異なる信号の比になります。入出力が比例関係にある諸元をこのような形で対数表現(定義)することにより、伝送線路上の電力から空間電力密度、電気エネルギーから音波のエネルギー等、形態の異なるエネルギーのレベル推移を一本のレベルダイヤグラム上で連続的に取り扱うことが可能になります。
なお、表2においてNo4のマイクロホン感度とNo5のスピーカ能率の定義には対数と真数が混在しているので注意が必要です。これらの諸元は入力値(マイクロホンでは音圧[Pa]、スピーカでは電力[W]の値が変化したときは、真数に換算してから変換されるレベルを導出する必要があります。色々調査しましたが、マイクロホンとスピーカについては、これ以外の単位は使用されていないと思われます。もしご存じの方がおられましたらご教示頂けますと幸いです。
5. エネルギー(電力)のデシベルと振幅(電圧)のデシベル
第2話において「dB(デシベル)とは電力利得(Power gain: GP)を表す「B」(ベル)という単位に、1/10を示す補助単位「d」(デシ)を組み合わせたもの」と解説した通り、デシベル(ベル)とは「電力の比の対数」を表す単位です。一方で我々が日常様々な計測器で直接観測できる諸元は電圧や電流などの「振幅」であって、電力のような「エネルギー」は電圧や電流など「振幅」の測定結果から間接的に導出することが通常です。このため表1に示したdB○×の中にも電力の単位と電圧の単位が存在します。但し、両者の間には決して一緒にできない隔たりがあります。
すなわち、「電圧が半分になっても電力は半分にならない」という問題です。
回路のインピーダンスが常に同じ前提で、電圧V、電流Iと電力Pのあいだには(式5-1)に示す関係があります。
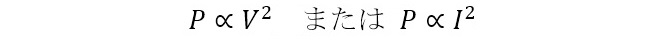
(式5-1)
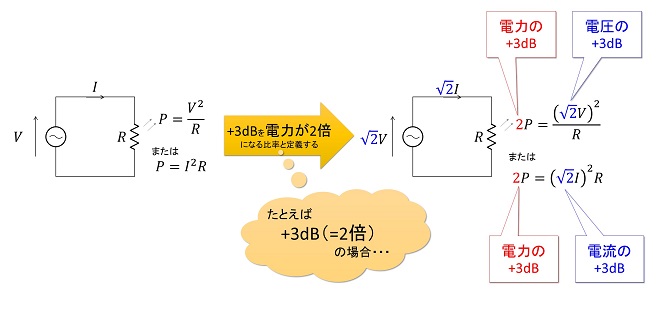
つまり電圧または電流が2倍になると電力は4倍の関係になるので、電圧、電流と電力を同じ定義でデシベルに変換すると電圧・電流が3dB増えたときの電力上昇値は6dBとなってしまい、両者は常に区別して取り扱う必要が生じます。これでは非常に不便になるため「dB(B)」の単位系では、図3に示すように電力の増分に比率が揃うように定義されています。
平たく言うと、電力の3dBが「2倍」なのに対して電圧・電流の3dBは「√2 」倍、演算処理としては電圧・電流の対数換算は電力に変換(2乗)してから対数にするという定義になっています。従って、電流、電流などの振幅系の諸元を示すdB○×は表1にかかれているとおり、
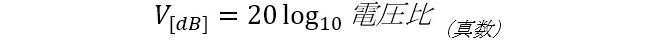
(式5-2)
のように係数が10ではなく20となっています。世の中のデータシートや文献では、振幅かエネルギーかを断り無くdBに換算して表示しているケースが多々あって、取り違えると計算が合わなくなります。SパラメータやNFなど、dBで表現されているが電力比なのか電圧比なのか非常にわかりにくい諸元というのも多くあって注意が必要です(特に表2に示した利得系のdB○×は、筆者も未だに迷います)。
自身でdBに換算するときも間違い易いので、単に10logか20logかという覚え方をするのではなく、常に「電圧・電流の比率は電力に換算してから対数にする」と言う基本を覚えておく事が大切だと思います。
6. 第3話のまとめ
第3話では、世の中に溢れかえっているdB○×という単位が何者なのかと言うことと、そのような単位が重宝される理由、ならびにエネルギー(電力)と振幅(電圧・電流)を同列に扱うために決められているデシベル界のルールとも言うべき10logか20logか・・・ の関係を解説しました。
10logと20logの使い分けは非常に解りづらく、ベテランエンジニアでも間違うことがよくあります。一般論で言うと伝送線路と空間伝搬に関するレベルダイヤグラムにおいて、縦軸の基本は[dBm]すなわち電力の次元です。これに対して測定器のアウトプットやデバイスのスペックは電圧比で書かれるケースが多くあります。これは前者がインピーダンス一定の伝送線路上での配分設計なのに対して、後者はインピーダンスが一定にならない回路上での波形の振幅に着目するためですが、そのあたりを理解しないでレベル配分、雑音配分を行うと現実離れした設計結果になってしまいます。振幅かエネルギーかという問題については、この後でも頻繁に登場することになりますので、必要に応じて都度解説することにします。以下、第3話の要点です。
- (1) dB(デシベル)が利得(比の対数)を表す単位(基本単位は [B](ベル))なのに対して、dB○×は電力や電圧の絶対量の対数を示す単位で、デシベルとは読まずデービー○×と読む。
- (2) dB○×という単位が必要な理由は、レベルダイヤグラムなどで対数変換した縦軸を用いる際、等間隔目盛で扱う事が出来る単位系の方が便利だからである。
- (3) dB○×には絶対量ではなく、比例関係があって形態の異なる2つのエネルギーの比を示すものが含まれる。
- (4) dB○×には電力を示すものと振幅をしめすものが混在する。電圧・電流などの振幅をdB○×に変換するときは、振幅を2乗してエネルギー(電力)の次元に変換した上で対数化する。言い換えると10log振幅比ではなく20log振幅比で対数値に変換する。これにより電圧のdBと電力のdBが同じ縦軸上で扱えるようになる。
次回は電力のデシベル[dBm]と電圧のデシベル[dBµV]について、さらに掘り下げて解説したいと考えます。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)