今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第25話 マイナスの周波数
2024年4月1日掲載
第24話までは、アナログ乗算の原理的な説明と、サイン波をかけ算すると何が得られるかをテーマにして、関連する無線機の定番回路の動作解説を行ってきました。まだ変復調について触れていませんが、いわゆる「アナログ方式」の無線送受信機の要素技術については、ここまでの解説で概ね網羅されたのではないかと思います。
第25話からは交流ベクトルとサイン波の関係に関する話題になります。交流理論では有効電力と無効電力、レジスタンスとリアクタンスのように、電圧と電流の位相差にまつわるベクトル空間が定義されています。この空間では位相差がベクトルの向きを決めるので、このベクトルとサイン波は切っても切れない関係になります。
1. マイナスの周波数
図1は第1話の図2の再掲です。サイン波同士のかけ算の結果がどうなるかを示す最も基本的な図で、周波数𝑓1のサイン波と𝑓2のサイン波をかけ算すると、振幅が半分で周波数が𝑓1と𝑓2の和のスペクトル、および振幅が半分で周波数が𝑓1と𝑓2の差のスペクトルに変換されることを示した図でした。
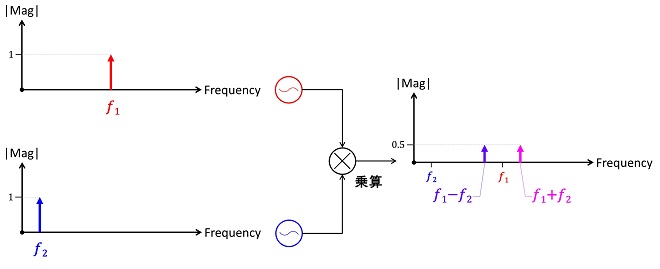
図1 振幅が等しく周波数の異なるサイン波をかけ算したときの周波数領域でのレスポンス
(第1話の図2の再掲)
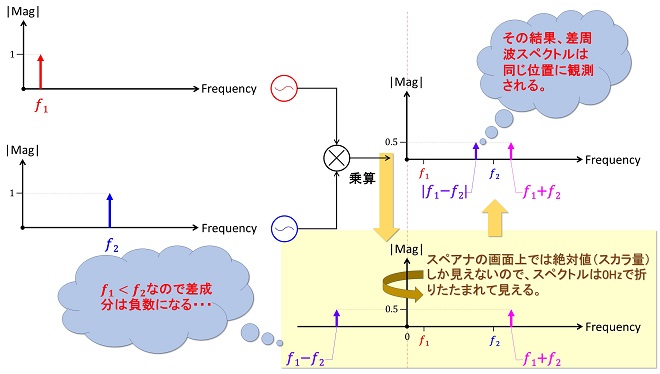
第1話では混乱を避けるために𝑓1と𝑓2の大小関係について、𝑓1<𝑓2すなわち図2に示すような場合については言及しませんでした。
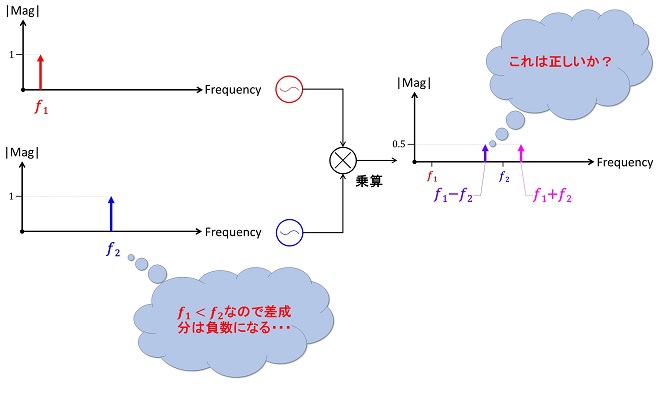
図2 振幅が等しく周波数の異なるサイン波をかけ算したときの周波数領域でのレスポンス2
(𝑓1<𝑓2となる場合)
図2の場合、第1話の(式2-5)~(式2-8)に従えば、差周波の成分は負の値になります。従って図2の右側の結果にはならないと思ってしまうのですが、実際に実験してみると𝑓1>𝑓2だろうと𝑓1<𝑓2だろうと関係なくスペアナの画面には図1(図2)と同じ結果が表示されるはずです。これはスペアナの周波数軸が「絶対値」であるため、図3に示すように0Hzを中心に正数側に折りたたまれたスペクトルを観察しているためです。
よく考えると、そもそも乗算回路(ミキサ)の入力端子には周波数の大小を判別する機能はありません。アナログ乗算器で行うサイン波のかけ算はスカラー演算であり、また周波数は絶対値でしか観測できません。従ってミキサ回路で周波数𝑓1のサイン波と𝑓2のサイン波の合成信号を非線形増幅(またはスイッチング動作)させた場合、出力される差周波成分については𝑓1-𝑓2の演算結果なのか𝑓2-𝑓1の演算結果なのか区別することはできません。
2. よくある認識
では図3に示した「マイナスの周波数」と「プラスの周波数」は一体何が違うのでしょうか?
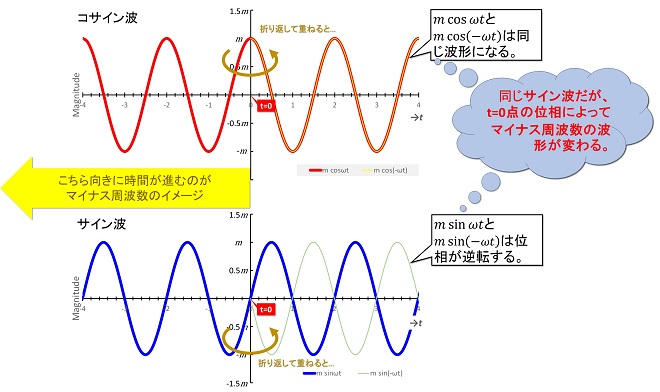
マイナスの周波数に関するよくある認識は、「時間経過とともに位相角が増えるのがプラスの周波数、時間経過とともに位相角が減るのがマイナスの周波数」というものです。筆者も高校の授業でそのように教わって納得していました。これを波形のイメージで捉えると図4のようになります。
サイン波を文字通り「m sin ωt」と捉えると、 「m sin (-ωt )」は 「m sin ωt」の逆相信号、 つまり「m sin (ωt +π )」と等しく見えます。 これに対してサイン波を「m cos ωt」と捉えると、 「m cos (-ωt )」は 「m cos ωt」の同相信号、つまり同じ信号に見えます。ここで二つの疑問が浮上します。
(1)マイナスの周波数=位相反転か?
→サイン波だけ考えると正しいかもしれないが、コサイン波はどう考えればよいのか?
(2)そもそもサイン波とコサイン波は何が違うのか? 位相が90°ずれているだけなのに、マイナス周波数の振る舞いが違うというのはどういうことか?
実は交流信号を「サイン波」として一次元量の時間変動(スカラー量)と捉えると、この疑問は解決しません(というか意味を持ちません)。スカラー量の世界では、位相は単にタイミングの違いであり、波形は同一なのでプラスの周波数もマイナスの周波数も区別できないのです。
3. 交流ベクトル空間
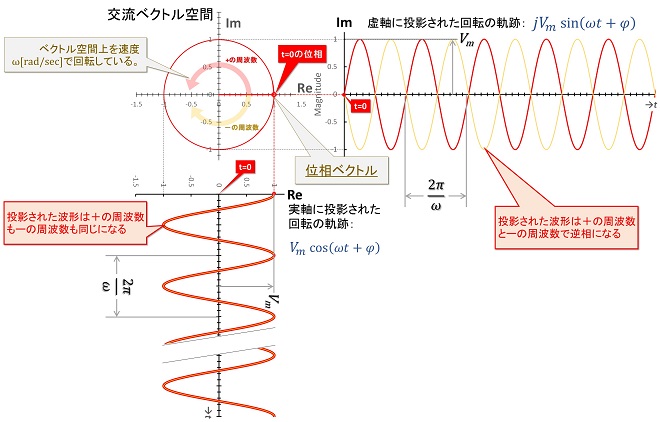
先ほどの2つの疑問は図5に示すように、位相を極座標系で表現された交流ベクトルの方位角として認識すると理解することができます。話がそれますが、三角関数はその名の通り直角三角形の内角と各辺の比の関係を示す関数として中学校(最近は高校らしいですが)で学び、その後高校で回転(円)運動との関係を学びます。このタイミングで三角関数は直角三角形から2次元のベクトル空間を表現する関数に進化するのですが、明示的に「ベクトル量」として取り扱うようになったのは、もっと後になってからだったかもしれません。
交流ベクトル空間は交流電圧、電流、電力それぞれの空間、またはそれらが共存する空間ですが、以下、交流電圧を例にとって解説します。図5の左上に示す通り、交流電圧は大きさVm のベクトル量で、交流ベクトル空間で常に一定の速度で回転しています。電圧ベクトルの回転中心を0点として極座標で表現したときの方位角、すなわちベクトル軸とx 軸のなす角φを位相(位相角)と呼びます。この図はt=0[sec]の瞬時電圧ベクトルを示しており φ=0[rad]です。 電圧ベクトルは周期ω[rad/sec]で回転します。我々がオシロスコープで観測するサイン波、コサイン波は電圧ベクトルの回転運動を一次元空間に投影したもので、コサイン波が実軸(Re軸)の投影、サイン波が虚軸(Im軸)の投影になり、それぞれ(式3-1)、(式3-2)で表現されます。
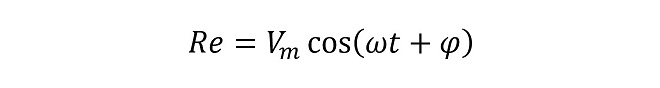
(式3-1)
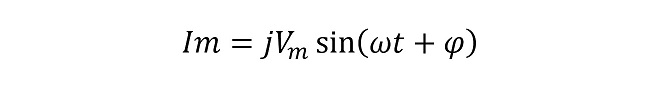
(式3-2)
(式3-1)、(式3-2)においてVmは電圧ベクトルの絶対値ですが投影波形では最大値となります。括弧の中は両方の式ともに同じ値が入ります。ωは角周波数(または角速度)で周波数𝑓に2π[rad]をかけた値、すなわち電圧ベクトルの回転の速さであり単位は[rad/sec]。これに時間tをかけてやることによって、時刻0からtまで累積で何ラジアン位相が進んだか(電圧ベクトルが何回転したか)を示す値になります。 φ は電圧ベクトルとRe軸のなす角で、時刻t=0における値を示しています。 ωt +φ で電圧ベクトルの時刻tにおける瞬時位相を示しています。我々は一般に このφを「位相」と呼んでいます。
4. 改めてマイナスの周波数とは
察しの良い方なら、ここまで述べればマイナスの周波数とはどういうものか理解されたのではないかと思います。マイナスの周波数とは(式3-1)、(式3-2)のωにマイナスの値が代入されたものです。周波数をサイン波の繰り返し周期ではなく電圧ベクトルの回転周期と捉えた場合、プラスの周波数とは回転方向がCCW(反時計方向)の電圧ベクトル、マイナスの周波数とは回転方向がCW(時計方向)の電圧ベクトルということになります。回転方向がCWの電圧ベクトルの実軸、虚軸それぞれへの振幅投影は図5のグラフに黄色でプロットしたとおり、実軸(コサイン)側はプラスの周波数と同じ、虚軸(サイン)側はプラスの周波数と正負逆の振幅になります。これで図4の謎は概ね解けたのではないかと思います。
5. ベクトル位相とオイラーの式
以上解説の通り、交流電圧・電流はベクトル値であり、(式3-1)と(式3-2)の和で表現されます。
交流電圧の場合だと・・・
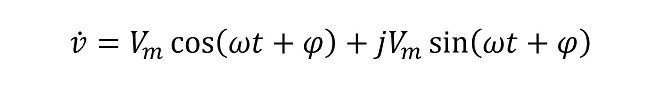
(式5-1)
この式はオイラーの公式:ε jθ = cosθ + j sinθ を適用して(式5-2)のように表現することが可能です。
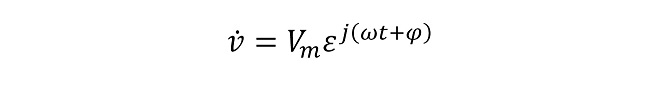
(式5-2)
オイラーの公式は高校の数学で学ぶ内容であり、式の証明については多くの文献やネット上の記事に解説がありますので、ここでは省略します。この式を用いると、三角関数で表現される交流電圧(電流)の瞬時値が指数関数となり、かけ算を繰り返すときに便利なため、交流電圧の表記としては頻繁に登場します。
6. 第25話のまとめ
第25話ではマイナスの周波数を題材に、交流ベクトルについて解説しました。以下、第25話の要点です。
(1)交流電圧(電流) Vm cos (ωt +φ ) (電流の場合は
Im cos (ωt +φ )は、
大きさVm、角度φのベクトルが角速度ωで回転している「ベクトル量」である。
(2)プラスの周波数とは瞬時値ベクトルが反時計方向に回転、マイナスの周波数とは瞬時値ベクトルが時計方向に回転している状態を示している。
第24話までは全て交流波形をスカラー量の「サイン波」として扱ってきました。一方で交流電圧と電流の世界では電圧と電流の位相が必ずしも一致しないので、交流電力は有効電力と無効電力の成分から成るベクトル量です。「周波数」は絶対値で定義される値ですが、交流ベクトルの空間においては電圧/電流ベクトルの回転速度としてベクトルを表す式に取り込まれるので、位相の回転方向という概念に基づいてマイナスの周波数が定義されます。世間では「マイナスの周波数」というものが本当に存在するのか? という議論がありますが、これはベクトル空間でサイン波を取り扱うときの概念の話であって、実際にマイナスの周波数だけを区別して観測することはできません。虚数と同じで、あるかないかと言う議論においては、概念として定義しているので「ある」という結論になりますが、観測できるかできないかという議論では「観測できない」ということになります。第26話では引き続き交流ベクトルとサイン波の関係ついて解説します。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)