今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第11話 ギルバートセル乗算器(その3・ギルバートセル乗算回路)
第10話までのお話で、ギルバートセル乗算器の要素回路である差動増幅回路と定電流回路、カレントミラー回路の動作について、理解を深めて頂けたと思います。随分回り道をしましたが、第11話ではギルバートセル乗算器全体の動作について解説します。
1. トランジスタで掛け算を行う方法※1
本題に入る前にトランジスタ(FET含む)による掛け算の基本的な考え方を説明します。
トランジスタを用いた乗算回路(ミキサ回路ではない)の基本は図1に示すような「カスケード(縦続)接続」です。トランジスタをこのような接続で使用すると、コレクタ電流の交流成分ΔICには、ΔVB1とΔVB2の積の成分が生じます。デュアルゲートのMOSFETにおいても同様の動作となります。
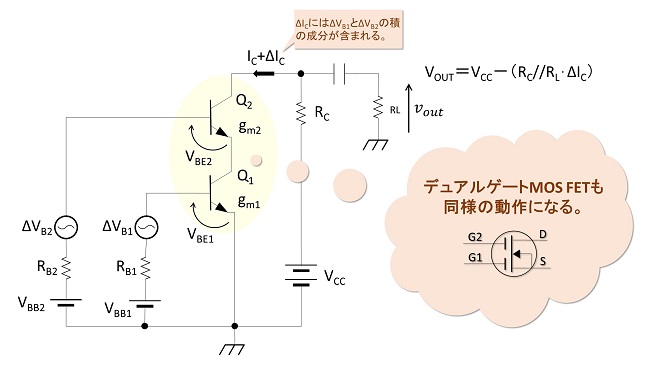
図1 トランジスタを用いた掛け算の概念図
これは、トランジスタのgmがコレクタ電流ICに比例するという特性によるものです。gmとは相互コンダクタンスの事で(式1-1)に示す通り、VBEの変化に対するICの変化の割合を示します。電圧/電流なので抵抗の逆数つまりコンダクタンスであり、単位は[S](シーメンス)です。

(式1-1)
トランジスタのベース-エミッタ間電圧VBEとコレクタ電流ICの関係は、ダイオードの電圧-電流特性と等価と見なす事ができ、近似的に(式1-2)の関係になります。
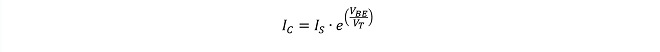
(式1-2)
ここでISはベース-エミッタ間の逆方向飽和電流でトランジスタ毎に異なる値(小信号トランジスタの場合で1×10-14[A]程度)、VTは熱電圧で(式1-3)で与えられます。
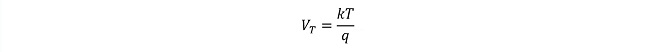
(式1-3)
k : ボルツマン定数(1.38×10-23[J/K])、q : 電子の電荷(1.602×10-19[C])、T : 絶対温度で、T=300Kのとき、VTは約26[mV]です。図2は(式1-2)の関係をグラフにプロットしたもので、(式1-1)で与えられるgmはこのグラフの接線の傾きを示す事になります。
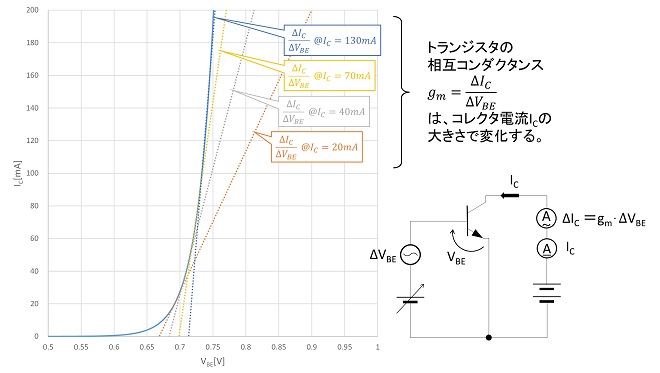
図2から判るように、トランジスタの相互コンダクタンスgmはコレクタ電流の大きさで変化し、コレクタ電流が増加すると大きな値になります。図3は図2のグラフの傾きを差分計算で模式的に算出したものです。相互コンダクタンスgmがコレクタ電流ICの関数になっている(比例している)ことが確認できます。
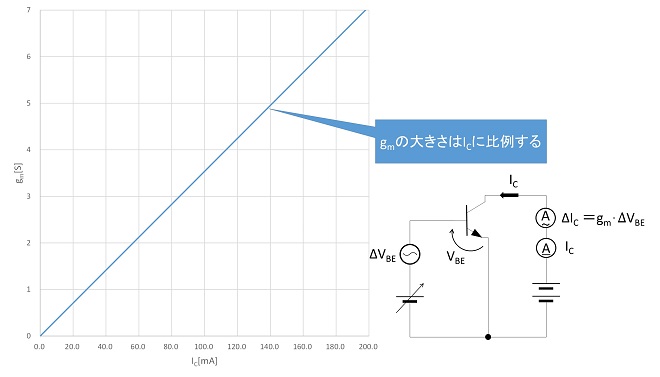
図3 トランジスタのICとgmの関係(図2の差分演算による導出)
相互コンダクタンスgmは、正確には(式1-2)をVBEで微分した値であり、
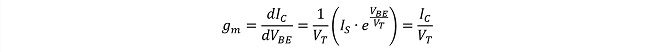
(式1-4)
の関係があります。gmはhfeと同様、トランジスタの小信号利得を決定するパラメータです。トランジスタがこのような特性を有する結果、図1のように2つのトランジスタをカスケード接続すると、コレクタ電流には2つのトランジスタのVBEの積に比例する項が含まれる事になりますが、図1のような単純なカスケード接続では2つのトランジスタのVBEの積に比例する項以外の項が同時に発生して分離が困難なため、もっぱらミキサ回路のように片方の信号(LO)が支配的に大きい関係での乗算や、カスケード接続とせずに直流バイアスを制御してICを増減し、可変利得増幅を行うというような使われ方が一般的です。
2. ギルバートセル乗算器※2
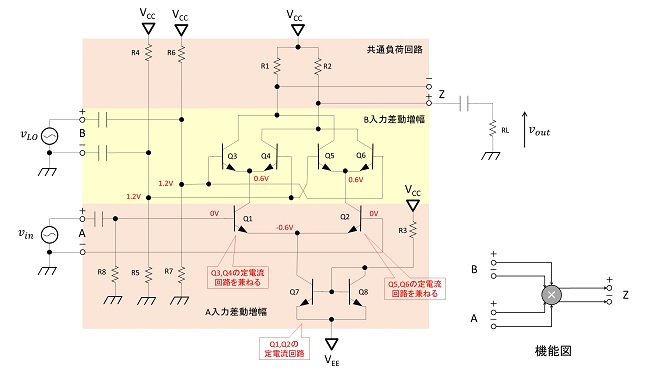
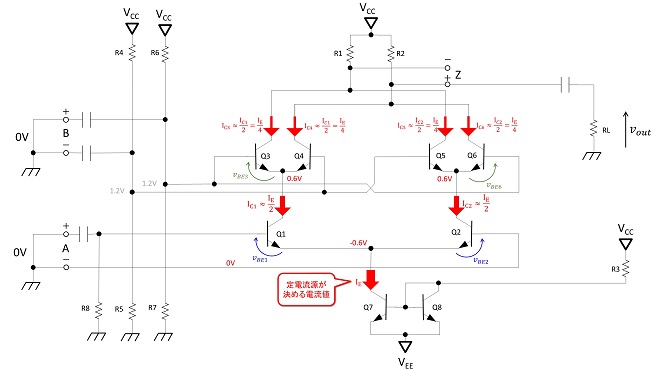
改めて、図4に直流バイアス回路を含むギルバートセル回路全体を示します。第1項ではトランジスタをカスケード接続しましたが、ギルバートセル乗算回路は第9話の図2でも触れたとおり、差動増幅回路をカスケード接続しています。すなわちQ1,Q2で構成されるA入力の差動増幅回路の負荷に、Q3,Q4、ならびにQ5,Q6でそれぞれ構成されるB入力の差動増幅回路を縦続接続した構成です。Q3,Q4の差動増幅回路とQ5,Q6の差動増幅回路の出力は共通の負荷抵抗R1,R2に接続されており、出力端子Zに対して並列接続された構成になっています。入力信号(B入力)は、Q3,Q4側とQ5,Q6側で+と-が、出力端子の極性と逆転する関係になっています。またQ7,Q8で構成されるカレントミラー回路はA入力の差動増幅回路の定電流源として機能し、A入力差動増幅回路を構成するトランジスタQ1,Q2は、B入力の2つの差動増幅回路の定電流源としての機能を兼ねています。
図4では、出力端子Zは+側(同相出力側)のみ使用していますが、機能図に示すとおり差動出力として取り出すことも可能です。
第9話で差動増幅回路の解説を行った時は、負電源VEEと定電流回路を用いる事で、ベース側にバイアス電圧を加える必要はありませんでしたが、ギルバートセル回路は、A入力差動増幅回路とB入力差動増幅回路が電源に対して直列に接続されたような構成になっているので、負電源VEEを用いていても、B入力差動増幅回路のトランジスタを増幅器として動作させる為には、ベース端子に直流バイアス回路が必須となります。図4では、バイアス回路設計の目安とすべき、トランジスタの各端子の電圧を赤文字で示しました。
A入力差動増幅回路のバイアス電圧は、カレントミラー回路Q7,Q8で生成され、入力端子(ベース)が0Vの時、Q1,Q2のエミッタは約-0.6Vに保たれます。
B入力差動増幅回路Q3,Q4とQ5,Q6のエミッタ端子はそれぞれA入力差動増幅回路Q1,Q2のコレクタ電圧と同電位になるので、Q3,Q4,Q5,Q6を線形増幅器として動作させるためには、各トランジスタのベース端子が、無信号時に0.6V以上のDCバイアス電圧が必要です。またQ1~Q6の無信号時VCEは大きい程、大振幅の信号が取り扱える事になります。
このため、図4ではQ1,Q2の無信号時VCE=1.2Vと定め、Q3,Q4,Q5,Q6の無信号時エミッタ電圧が0.6Vになるよう、ベースバイアス電圧をエミッタ電圧+0.6Vの1.2Vとしています。
3. 4象限乗算動作
第9話で述べた通り、ギルバートセルは4象限のアナログ乗算ができる回路です。すなわち
(式2-1)
(式2-2)
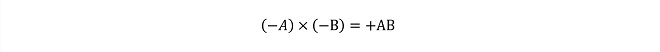
(式2-3)
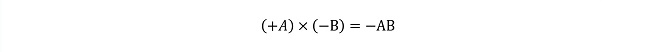
(式2-4)
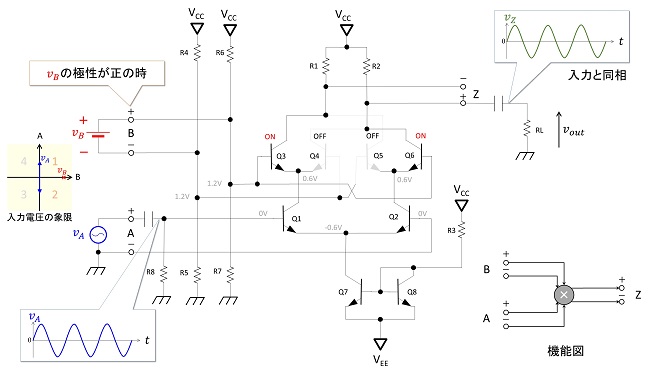
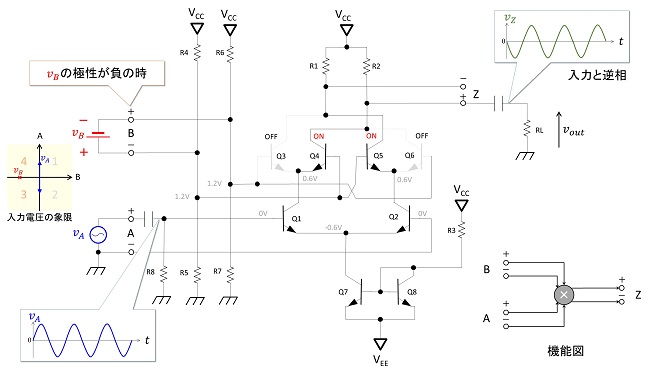
の4パターンの極性の組み合わせに対応した演算ができると言うことです。この様子を図5~図6で解説します。これらの図では話を簡単にする為にB入力に充分に大きな直流電圧を加えてQ3,Q4、Q5,Q6の各差動アンプを飽和させた状態、A入力(Q1,Q2)は線形領域の入力電圧で動作している状態を示します。
図5はB入力に+の電圧を加えて飽和させた状態です。この時はQ3とQ6がON状態、Q4とQ5がOFF状態となるため、Q1のコレクタはR1側(−Z端子)に、Q2のコレクタはR2(+Z端子)にそれぞれ接続された状態になって、Z端子にはA入力と同相の出力電圧が観測されます。この状態は(式2-1)と(式2-2)の演算すなわち、第1象限と第2象限の動作を示します。
図6はB入力に-の電圧を加えて飽和させた状態です。この時はQ3とQ6がOFF状態、Q4とQ5がON状態となるため、Q1のコレクタはR2側(+Z端子)に、Q2のコレクタはR1(−Z端子)にそれぞれ接続された状態になって、Z端子にはA入力と逆相の出力電圧が観測されます。この状態は(式2-3)と(式2-4)の演算すなわち、第3象限と第4象限の動作を示します。このようにQ1,Q2の各コレクタ電流をR1,R2どちらに接続するか(正確にはどちらに多く流すか)がB入力電圧の極性で決まる事によって4象限全ての乗算を行う事ができます。
4. A入力電圧とB入力電圧が乗算される仕組み
図5、図6の説明で、第7話~第8話で解説したDBMと同様、B入力を±1の信号としてA入力の信号に乗算できることはお解り頂けたと思います。続いてQ3~Q6がスイッチ動作ではなく、能動領域で増幅器として動作する状態を考察します。ここから先はバイアス成分と交流成分(1項でΔを冠して表現した成分)を区別するため、バイアス成分を大文字、交流成分を小文字で示します。
図7にA、B共に無入力(0V)の時の各トランジスタのコレクタ電流を示します。図中赤い矢印は各トランジスタのコレクタ電流で、軸の幅が相対的な電流の大きさを示しています。本図では第9話と同様、各トランジスタのIBはICに対して充分小さく無視できると仮定します。また各トランジスタの特性は完全に一致している前提です。
無信号時の各トランジスタのコレクタ電流ICはQ7のコレクタ電流(Q1,Q2の合成エミッタ電流という意味でIEと表記しています。)を基準に、Q1,Q2がその半分、Q3~Q6がさらにその半分となっており、Q7はQ1,Q2ペアの定電流源、Q1,Q2はそれぞれQ3,Q4とQ5,Q6の定電流源として動作しています。各トランジスタのgmはこの電流値で決定されます。
次にA入力、B入力に交流信号が入力された状態を図8に示します。図8ではA入力、B入力共に+の電圧が印加されている状態を示しています。
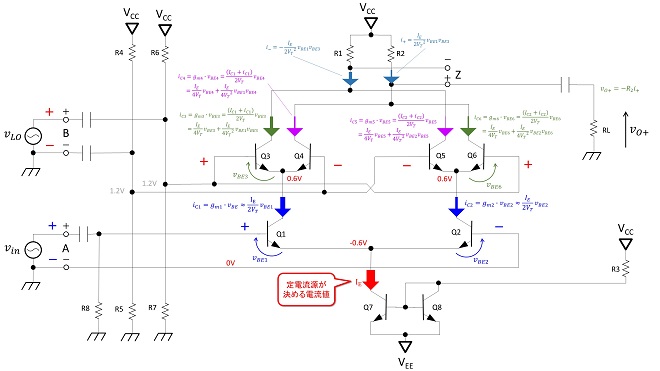
図8 A,Bに交流信号が入力された場合のギルバートセル乗算回路
この時、A入力差動増幅器Q1,Q2は第9話で解説した通り、𝑖C1が増加、相対的に𝑖C2が減少する事になります。またQ1,Q2の相互コンダクタンスをそれぞれgm1、gm2と置くと、𝑖C1,𝑖C2はそれぞれ(式1-4)から
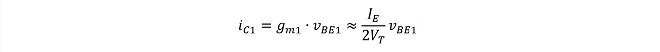
(式3-1)
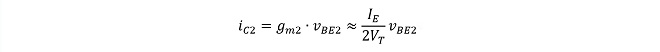
(式3-2)
またiC3~iC6は、Q3~Q6の相互コンダクタンスをそれぞれgm3~gm6とおいて、
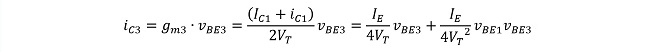
(式3-3)
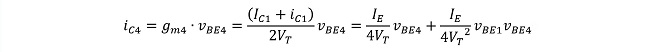
(式3-4)
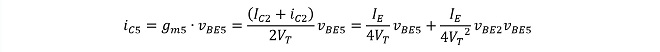
(式3-5)
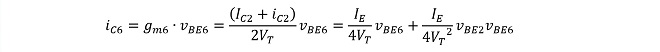
(式3-6)
となります。𝑖C3~𝑖C6の各電流は出力電圧を取り出す為に+側(R2側: 𝑖C4+𝑖C6)と-側(R1側: 𝑖C3+𝑖C5)にまとめられます。これらを𝑖+, 𝑖-と置くと
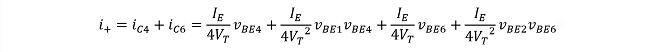
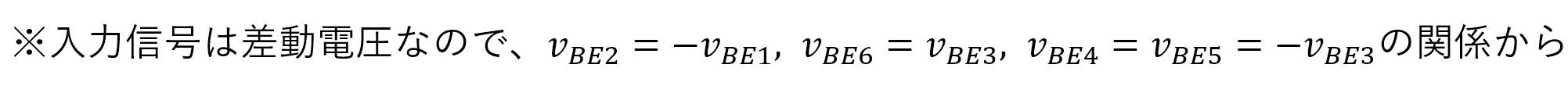
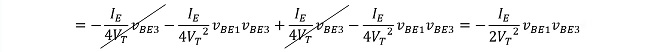
(式3-7)
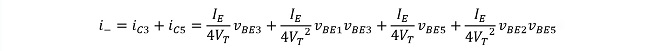
※同様の関係から
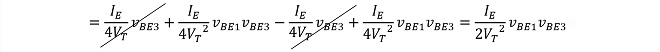
(式3-8)

5. 第11話のまとめ
ギルバートセル乗算器の動作をご理解頂けましたでしょうか。ギルバートセル乗算器はアナログICの内部回路で多用されており、精度の良い乗算ができる事が特徴です。一方で電源電圧の半分以下の振幅で飽和してしまうという電源電圧利用率の悪さが弱点になります。この弱点は電源に対して増幅回路を縦続(カスケード)接続するために生じるもので、カスケード型の増幅器共通の泣き所です。このためギルバートセル回路は受信機の周波数変換回路等、ダイナミックレンジが要求される用途には向きません。どちらかと言うと変復調回路など、演算精度が要求される機能ブロックで多用されています。以下に第11話の要点をまとめます。
(1) トランジスタの相互コンダクタンスgmはコレクタ電流に比例する
(2) アナログ乗算は(1)の特性を利用し、トランジスタをカスケード接続することで機能を実現している。
(3) ギルバートセル乗算回路は差動増幅回路をカスケード接続して乗算機能を実現したものである。
1年を費やしてしまいましたが、世の中でよく使われる「乗算」回路の紹介と、サイン波の掛け算の初歩ともいえる「周波数変換」の解説は今回で終わりです。次回から「同一周波数の掛け算」とPLLについて解説します。
※1: 本項は以下の文献を参考にさせて頂きました。
① https://cc.cqpub.co.jp/system/contents/2312/
※2: 2項以降については以下の文献を参考にさせて頂きました。
① https://michaelgellis.tripod.com/gilbert.html
② 宮本幸彦 高周波回路の設計と実装 1987 日本放送出版協会 P113-P120
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)