第12話から第21話までは、同一周波数のサイン波の掛け算結果が位相差を示す事と、その代表的な応用例であるPLLについて解説してきました。第22話は同一周波数の掛け算の別の側面について解説します。

1. 同一周波数のサイン波の掛け算で得られるもの

図1は第12話の図2の再掲です。周波数の等しいサイン波どうしを掛け算すると、両者の位相差を示す直流成分と両者の周波数の2倍の周波数のサイン波が得られました。位相検波においては前者のDC成分を利用したわけですが、後者を利用すると周波数の2逓倍が可能です。

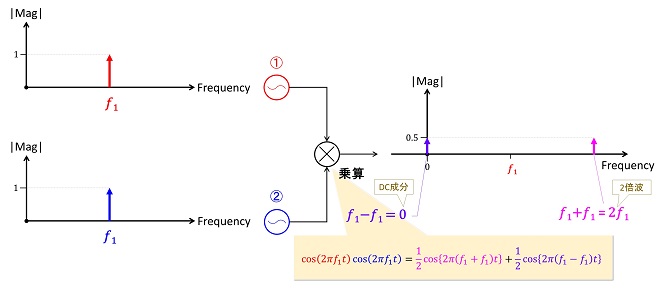
図1 同一周波数のサイン波どうしの掛け算(スペクトラム) (第12話 図2の再掲)

位相検波回路の場合は周波数の等しい2つの信号を掛け算しましたが、逓倍回路の場合は自分に自分を掛け合わせる･･･ つまり入力信号を2乗する回路を用いる事になります。(図2)

図2 サイン波のべき乗演算

2. 入力信号を2乗する回路

入力信号を2乗する為には、第7話で紹介したDBMや第9話で紹介したギルバートセル乗算器などの入力端子に同一信号を入力する事でも可能ですが、周波数逓倍回路においては、もっぱら第2話で解説した半導体PN接合の非線形特性が利用されます。

少しだけ第2話の復習です。半導体のPN接合の端子電圧V_F と端子電流I_j の関係(静特性の理論値)は(式2-1)で与えられます。

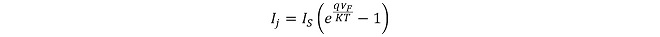
但し、I_S：逆電圧印加時の飽和電流[A]
K：ボルツマン定数=1.386×10^-23[J/K]
T：絶対温度
q：電子の電荷量=1.6×10^-19[C]
(式2-1)

つまり、PN接合に流れる電流の大きさは両端に加えた電圧の指数関数に比例します。これをグラフに表したのが図3の①の特性です。

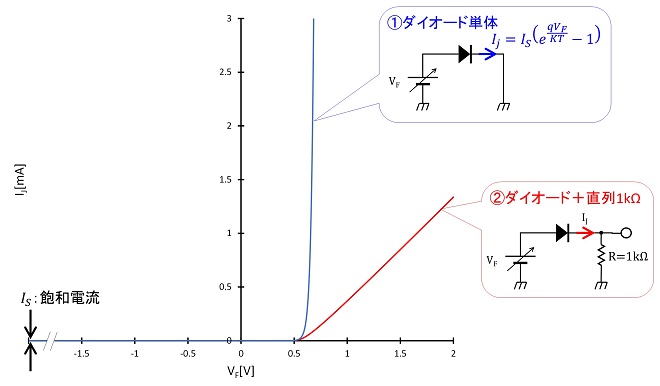
図3 PN接合とPN接合に負荷抵抗を接続した場合の電圧-電流特性

では、PN接合に正弦波電圧を印加した時の電流の大きさはどうなるでしょうか。指数関数はマクローリン展開によって、(式2-2)に示す多項式に展開する事ができます。

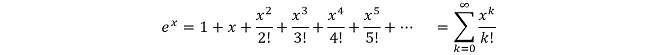
(式2-2)

例えばコサイン波で考えると、この級数の x に cos⁡(ωt ) が代入されることになるので、PN接合に流れる電流には印加したコサイン波電圧のn乗(n=1,2,3…)成分の波形が含まれる事になります。ではcosⁿ⁡(ωt )という波形にはどのような周波数スペクトルが含まれるのでしょうか。

コサインの2乗は同一周波数の2つの信号の掛け算ですから、これまで解説したとおり、DC成分と2倍波が生成されます。→ (式2-3)

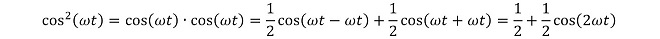
(式2-3)

コサインの3乗は、同一周波数の2つの信号の掛け算結果にさらに同一周波数の信号を掛け算した結果になるので、(式2-4)に示す通り、元の周波数成分と3倍周波数の成分が得られます。

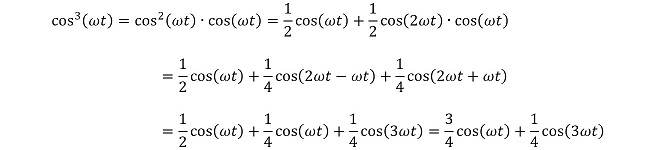
(式2-4)

このように、cos⁡(ωt )のn乗を展開するとcos⁡(nωt )が含まれるので、PN接合に正弦波電圧を印加すると、PN接合部にはその正弦波周波数のn倍の成分が含まれることになります。

従って、図3の②(赤の吹出し)に示すように直列抵抗を加えてPN接合を流れる電流を電圧に変換してやることによって、正弦波のn乗の成分を含む電圧を取り出すことが可能です。

3. ダイオードによるn乗回路

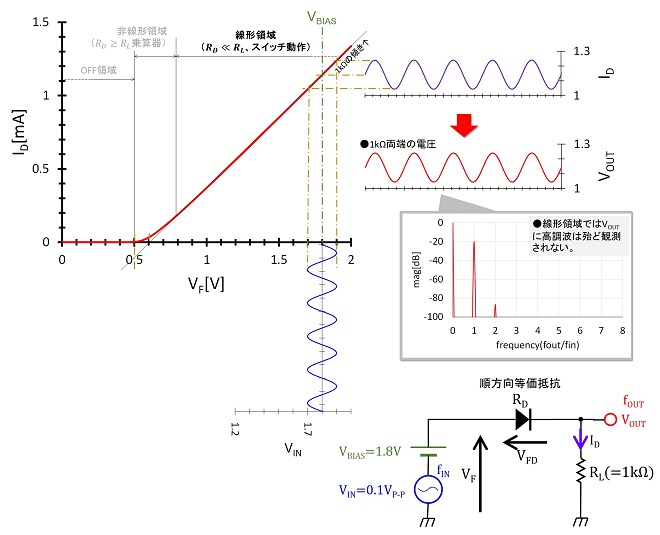
図3②に示したダイオードと1kΩの直列回路に正弦波電圧を印加して、n乗成分が得られる様子を回路シミュレータで見てみることにします。回路は図4､図5に示すように、図3②の回路にAC電圧源VIN を直列接続した構成です。VBIASは直流バイアスで入力サイン波の振幅中心を回路のVF-ID特性グラフのどこに固定するかを定めます。図4に示すように、VBIASの値がVF-ID特性上の“線形領域”にあるときは、ダイオードの順方向等価抵抗R_D (=V_FD /I_D )が直列接続されたRLに対して充分小さい領域(R_D ≪ R_L )なので入力されたAC電圧VINは歪まずにそのままVOUTとして観測されます(スイッチ動作。VBIASが正極性でON、負極性でOFF）。

これに対して図5に示すようにVBIASの値がVF-ID特性上の“非線形領域”にある場合は、接合部の順方向等価抵抗R_Dが直列接続されたRLに対して無視できない大きさの領域(R_D ≥ R_L )なので、出力電圧VOUTはVINの指数関数となります。図5のVINとVOUTの関係は、この非線形領域の動作を示しており、出力電圧VOUTはVINとは大きく異なる波形になっています。この歪んだ波形をフーリエ解析したものが図中、右上の吹出しの中にあるグラフで、DC成分とVINの周波数fIN以外にfINのn倍のスペクトルが発生していることが判ります。

図4 ダイオードを用いたスイッチ回路

図5 ダイオードを用いたn乗回路

4. 第22話のまとめ

第22話では同一周波数のサイン波の掛け算の応用として周波数逓倍を紹介し、ダイオードによる周波数逓倍動作について、ダイオードのスイッチ動作と比較するかたちで解説しました。3項で解説したn乗回路の出力にバンドパスフィルタを設けて、所望の高調波のみを取り出すようにした回路が周波数逓倍回路です。以下、第22話の要点を整理します。

(1) 三角関数(sin ωt、またはcos ωt )をn乗するとn×ωtの成分が生成される。
(2) 周波数逓倍回路は、PN接合部を流れる電流が電圧の指数関数(＝べき乗の級数)になることを利用して実現する。
(3) ダイオードに直列抵抗を挿入し、PN接合部の電流に比例した電圧を取り出す回路においては、印加電圧(バイアス電圧)の大きさにより、ダイオードの電圧降下が支配的になる非線形領域と直列抵抗の電圧降下が支配的になる線形領域に分かれる。
(4) 周波数逓倍回路は入力電圧をべき乗演算するので、入力電圧の振幅が上記の非線形領域に入るようにバイアス電圧を調整する。
(5) これに対して入力電圧の振幅が線形領域に入るようにバイアスするとダイオードはスイッチとして動作する。

一般に、抵抗を直列に挿入して電圧を取り出す方式の回路では、PN接合の非線形領域が狭くなるため、ダイオードを用いた逓倍回路は逓倍出力が小さくなります。このためトランジスタやFETが利用できる場合は逓倍増幅回路が多く用いられます。次回はトランジスタを用いた逓倍回路について解説します。