今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第27話 交流ベクトル空間と直交ミキサ(その2)
2024年6月3日掲載
第26話では、直交ミキサの構成と動作原理について解説しました。第27話ではここで言うサイン波の「直交」とは具体的にどういう意味で何に使えるのかについて解説したいと思います。今月も少々回り道の解説になるかもしれませんがお付き合い下さい。
1. cosθとsinθは直交している
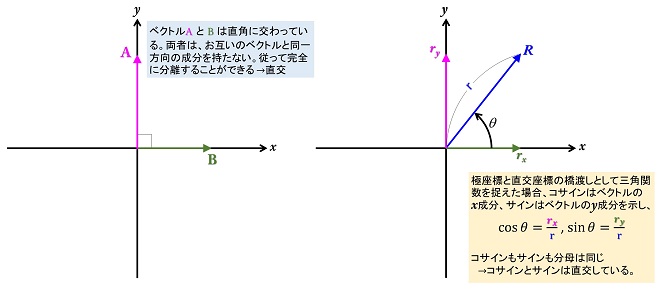
そもそもベクトルの「直交」とはどういう意味だったでしょうか。中学の数学では「2つのベクトルのなす角が直角であることを示す。」と習いました。高校数学では「2つのベクトルの内積が0になる事」と学びました。図1の左側に示すように、互いに直交しているベクトル同士は相互に相手のベクトルと同一方向の成分を有さないため、同時に存在してもお互いに干渉しません。
第26話ではコサイン波(cosθ)とサイン波(sinθ)は直交している前提で話を進めました。このことは図1の右側に示すように極座標と直交座標の変換を考えれば理解できるのではないかと思います。すなわち極座標で表記されたベクトルR = r∠θ を直交座標に変換すると、x 成分rx = r cosθ、y 成分ry = r sinθ、またr はベクトルR の絶対値、すなわちスカラー量であることから、cosθ、sinθはそれぞれx軸、y軸と同じ方向のベクトル量であり、両者は直交していると考える事ができます。つまりLO信号としてcos波とsin波を使用する直交ミキサとは、「入力信号を直交しているLO信号と乗算するミキサ」と言うことができます。
2. 直交ミキサの用途
直交ミキサには、主に以下の3つの用途があります。
① 同一周波数で直交した2つの搬送波信号を、それぞれ異なる伝送信号で変調する。
(直交変調)
② 直交変調された信号に直交したLOを乗算することで、2チャネルの伝送情報を取り出す。
(直交検波)
③ 入力された交流信号とLOの乗算出力から和周波成分、差周波成分を分離して取り出す。
(イメージリジェクションミキサ)
このうち第25話で解説した「マイナスの周波数」を直接取り扱っているのは③項になりますが、27話では①②について、Excelを用いて波形を計算しながらコサイン波とサイン波が直交していると言うことについて理解を深めることにします。(今月は作図に用いたExcelシートを提供します。詳しくは文末を参照ください)
3. 直交変調するとLOの波形はどのようになるか
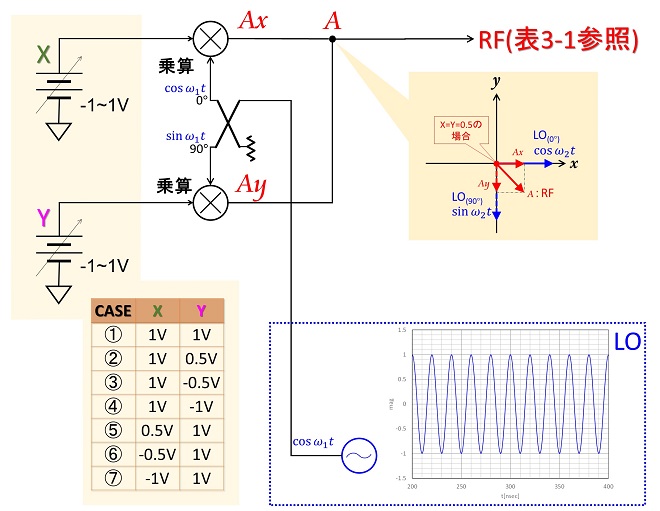
このようなタイトルを書くと、コサイン波とサイン波は直交しているので、足し合わせても両者が区別できるような特徴のある波形になると期待しがちですが、コサイン波とサイン波を足し合わせても、コサインでもサインでもない“正弦波”になるだけです。図2に直交変調回路のイメージ図を示します。
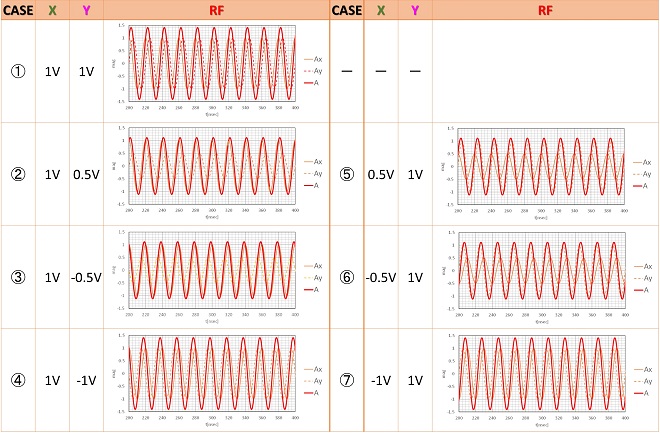
LOは1周期20[nsec]のコサイン波(つまり周波数50MHz)で、これを90°分配器で分配する事によりコサイン波、サイン波を得ています。コサイン波を入力した乗算器のもう一方の入力をX、同、サイン波を入力した乗算器のもう一方の入力をYと定義し、ここに±1Vの範囲の直流電圧を組み合わせを変えて加えた時にRF出力の波形がどのように変化するかを計算したのが表3-1です。
表3-1のCASE列に示した番号は、図2の入力側に示したCASE番号と同じです。グラフにはX側乗算器の出力AxとY側乗算器の出力Ayならびに両者の合成出力波形A(RF端子での観測波形)を重ねて表示しています。図から読み取れるように、直流電圧をかけ算することにより、Ax、Ayに現れるLO信号は、位相はそのままでX,Yに入力される電圧に比例して変化します(当然、X,Yにマイナスの電圧を加えたときは位相反転します)。これらを足し算すると、両者の振幅に応じて合成振幅と位相は変化しますが、周波数に変化はなく、やはり「正弦波」です。しかし図2のベクトル図からも判るように、RF端子に現れる信号の位相と振幅は、X,Y端子の電圧と1対1で紐付けされ、X,Y端子の特定の電圧の組み合わせと別の電圧の組み合わせが、RF端子において同じ振幅と位相になることはありません。これはコサイン波とサイン波が直交しているためです。
4. 直交変調されたRF信号を直交ミキサで周波数変換すると出力波形はどのようになるか
では、直交ミキサでX,Y各端子の電圧と紐付けされたRF信号を直交ミキサで周波数変換するとどうなるのでしょうか。まずは話が簡単な同一周波数での周波数変換を考えます。
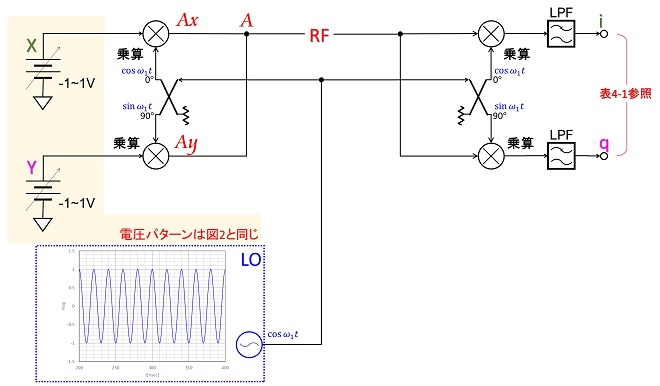
図3はRF信号に同じLO信号(周波数も位相も揃った信号)をかけ算したケースです。この回路は「同期検波回路」の原理説明で良く使われます。同一周波数のサイン波をかけ算すると、位相差に対応した直流電圧と2倍波が得られるというのは、これまでに何度か解説した通りです。図3の回路では、右側の直交ミキサの2つの乗算器の各出力に、それぞれLPFを挿入して2倍波成分を除去し、直流成分のみを取り出しています。コサイン側の出力をi、サイン側の出力をqとしています。
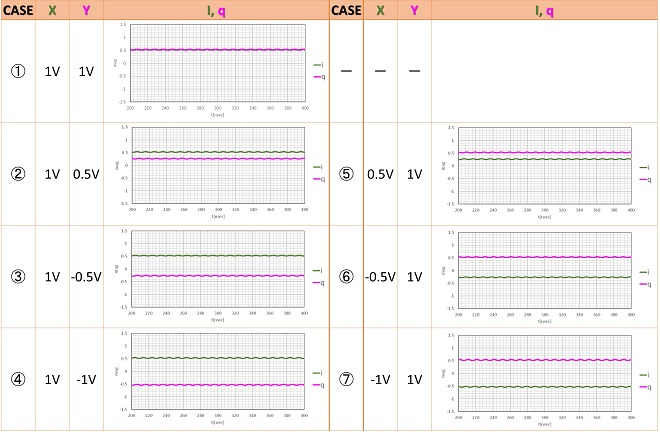
左側の直交ミキサの入力X,Yに図3と同じパタンで入力電圧を加えた時、右側の直交ミキサ出力i,qにどのような出力が現れるのかを整理したのが表4-1です。
表4-1のCASE列に示した番号とX列、Y列の電圧値は、図2の入力側に示したCASE番号と各電圧値に対応します。グラフは図3の受信側(右側)乗算器のコサイン側乗算出力iとサイン側乗算出力qが表示されています。グラフが少々波打っているのはLPFの減衰量が不足して2倍波成分が残っているためです。グラフのi、qの電圧値とX列、Y列の電圧値を見ると、iがX、qがYに対応して増減しており、その関係は
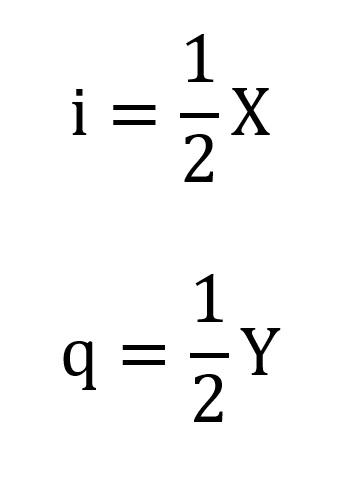
(式4-1)
になっていることが読み取れると思います。振幅が半分になるのはi,q端子に現れる信号が乗算結果の差周波成分だけであるためで、三角関数の加法定理(第1話の(式2-5)~(式2-8))が示す通りです。このように表3-1ではコサイン成分とサイン成分の識別はできない状態でしたが、第26話で解説した通り、送り側と同じ位相(タイミング)で直交サンプリングすることにより、X成分、Y成分はちゃんと分離して取り出すことができました。
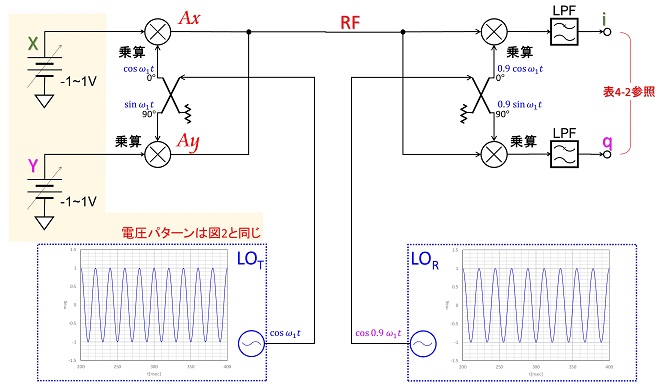
次に異なる周波数のLO信号で周波数変換するとどうなるでしょうか。ここではダウンコンバートの例で計算してみます。図4に計算に使用した処理構成を示します。
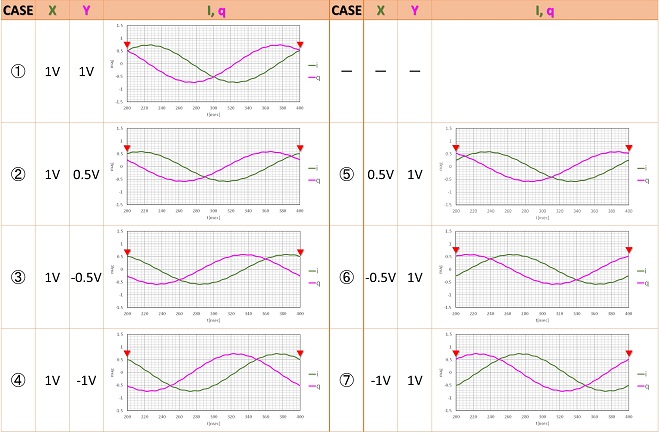
図4の送信側(左側)は図3と同じですが、送信側と受信側でLOの周波数が異なるので、識別できるようにLOT、LORとしています。50MHzのLOTに対してLORは0.9倍の周波数、すなわち45MHzとしました。LOTとLORは周波数が異なるので位相差の議論はできませんが、時刻t=0secにおける開始位相はどちらも0°から開始しています。右側の各乗算器の出力には、それぞれ位相の異なる5MHz(差周波)の成分と95MHz(和周波)の成分が出力されます。ここからLPFで差周波の成分のみ取り出して、それぞれi(コサイン側)、q(サイン側)としています。i、qともにDC成分ではなく、かつRF(=LOT)と周波数も異なるので、Ax、Ayのそれぞれ位相や振幅がそのまま読み取れないことは察しがつくのではないかと思います。計算した結果を表4-2に示します。
表4-2のi,q信号波形は周期200nsecの正弦波になっており、周波数が5MHzであることが判ります。振動しているので表4-1で見たようなX,Yとの対応関係を確認するのは難しいそうですが、各グラフ上に「▼」で示した部分、すなわち時刻0secから1周期毎のタイミングの電圧は、表4-1と同じになっていることがわかります。つまりX,Yの情報は変換された差周波成分のの時刻t=0(の1周期毎)の瞬時位相に反映されます。
5. 第27話のまとめ
このように同一周波数のコサイン波とサイン波は直交しており、別々の信号として分離することが可能です。昨今のデジタル通信で多用されている直交位相変調(QPSK)、直交振幅変調(nQAM)等“Q”を冠した変調方式は、このコサイン波とサイン波の直交性を応用して同一周波数で2ビット(2チャネル)の伝送を行う変調方式です。マイナスの周波数と交流ベクトル空間から話を始めた「コサイン波とサイン波の直交」という話題ですが、今月はこれを解説するに際し、どのように説明をするのが良いか悩んだ結果、いったん交流ベクトル空間から離れて、直交変復調の話を取り上げました。これで直交のイメージが伝われば幸いです。
以下、第27話の要点です。
- (1) 同一周波数のコサイン波とサイン波は直交しており、合成されても分離して取り出すことが可能。
- (2) コサイン波とサイン波が合成された信号に、周波数と位相(0°のタイミング)の揃った直交信号(LO)をかけ算する事で両者を分離して取り出すことができる。
- (3) 周波数の異なる直交LOをかけ算して周波数変換したときは、t=0から1周期毎に送り側のコサイン波とサイン波の情報が抽出できる。
ここでは話を簡単にするために絶対時刻(t=0)を定義して解説しましたが、これらは実際にはすべて相対的な時間(位相)関係の中で成立しています。送信側と受信側で絶対時刻が合っていなくても、送受双方のコサイン波とサイン波の直交性はそれぞれ保たれていますが、送信側と受信側で時刻がずれている分だけ実軸と虚軸(図1ではx軸とy軸)全体が傾く(回転する)ことになります。そのため、実際のデジタル通信では絶対時間(t=0)を示す符号をあらかじめ送り側に組み込んでおき、受信側で軸の回転を補正する操作を行います。
次回は交流ベクトル空間に話を戻して、イメージリジェクションミキサについて解説します。
付録 本稿で用いた表計算とLPFについて
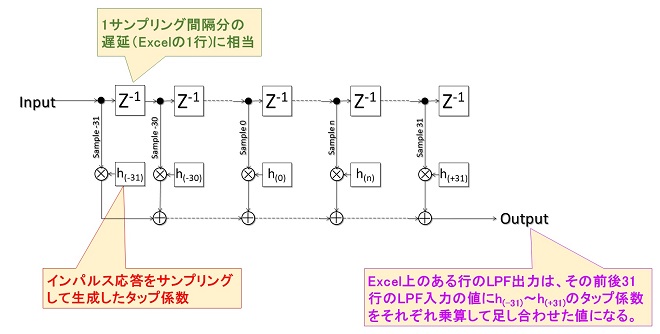
図3、4に登場したLPFは、63タップのFIRフィルタをExcel上で模擬したものです。本稿に用いた表計算ではすべての信号を1nsecの間隔で0sec~2154nsec(2048以上としただけで2154に特に意味はありません)まで計算しており、そのうち200msec~400msecの間を切り出してグラフにしています。 200msecという時間の長さは差周波成分である5MHzの1周期に相当し、かつ絶対時刻200msec,400msecというポイントは、初期位相(時刻0msecの位相差情報)が繰り返されるポイントを始点としたものです。FIR LPFは図5に示すような処理構成で、表計算のイメージで平たく言うと、あるサンプリングポイント(Excelの各行)の出力は、その前後31行の入力値に所定のタップ係数を乗算して合計した値で、これを毎行計算した結果をLPF出力としています。
h(-31)~h(+31)のタップ係数は、図6左下に示したLPFの所望の周波数特性を逆フーリエ変換して得られた時間応答波形をサンプリングクロックの間隔(ここでは1nsec間隔)でサンプリングしたものです。従って、本フィルタのインパルス応答特性を示したものです。このタップ係数で実際に得られるLPFの特性は、再度タップ係数をフーリエ変換することで求められ、図6の右上に示すグラフのようになります。
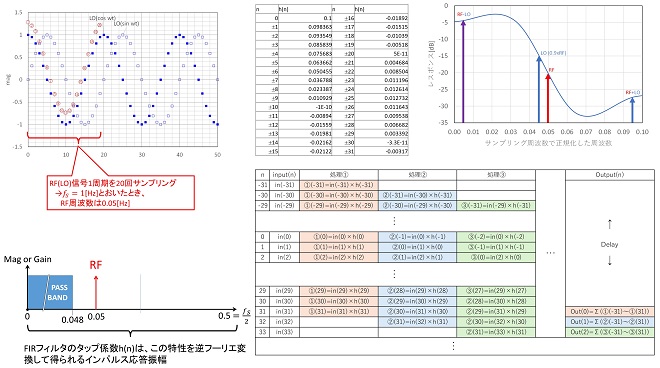
図6 表計算のサンプリングイメージとFIRフィルタのタップ係数、減衰特性
計算に用いたExcelファイルをこちらからダウンロードできるようにしてもらいますので、興味のある方は、Excelシートから計算内容をご確認下さい※。
- ※ダウンロードされたExcelシートに関するご質問についてはご容赦ください。Excelシートの内容に関する知的財産権その他一切の権利は筆者濱田倫一に帰属します。月刊FB NEWS編集部は筆者濱田倫一の許可を得て本件記事を掲載しております。また筆者、ならびに月刊FB NEWS編集部は、これらExcelシートの二次使用に伴う一切の責任を負いませんので、あらかじめご了承ください。なおExcelは米国マイクロソフト社の商標です。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)