第9話では、ギルバートセル乗算器を構成する要素回路である差動増幅回路の動作について解説しました。差動増幅回路は2つの増幅回路のエミッタが共通の定電流源に接続される事によって、如何なる入力条件においても2つの入力端子に加わる電圧差のみに応答する増幅回路として動作します。これを別の言葉で言い換えると、2つの入力端子に同電位の電圧を入力した場合、その値が何Vであっても出力電圧は変化しない増幅回路となります。オペアンプ等ではこの性能の善し悪しを「同相信号除去比 CMRR: Common Mode Rejection Ratio」と呼び、差動増幅の性能を示す重要なパラメータの一つです。このCMRRの大きさ(良さ)は、差動増幅回路を構成する2つの増幅器の特性がどれだけ一致しているかと、エミッタに接続された定電流回路の性能に左右されます。第10話では定電流回路の動作について解説します。

1. 理想の定電流源

等価回路や回路シミュレーションの議論をしていると、定電圧源・定電流源という電源素子が頻繁に登場します。定電圧源は直感的に理解しやすいのですが、定電流源というのは、以外とピンとこない方が多いのではないでしょうか。大学時代の復習です。

図1 理想定電圧源と理想定電流源の特性

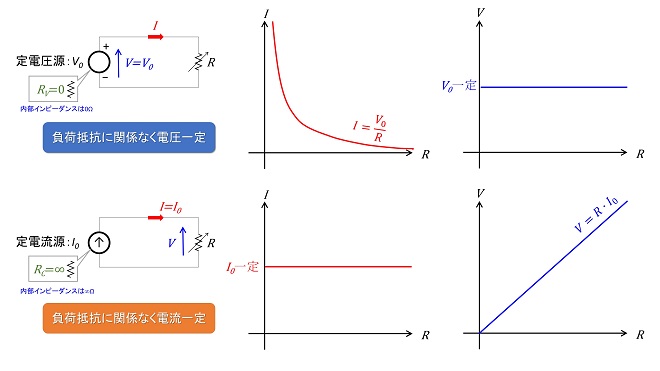
図1は理想定電圧源と理想定電流源の特性定義を示したものです。定電圧源は内部インピーダンスが0Ωでどれだけ電流が流れても端子電圧が変化しない電源素子です。従って図1の上側に示すように負荷抵抗Rを接続して、その値を0Ωから∞Ωまで変化させても電圧源の端子電圧VはV0一定で変化せず、回路電流は負荷抵抗Rの値に反比例して変化します。

定電流源は「定電圧源の裏返し」と理解・説明されるケースが多いですが、内部インピーダンスが∞Ωで端子電圧が何Vであっても自身に流れる電流値が変化しない電源素子です。従って図1の下側に示すように、負荷抵抗Rを接続して、その値を0Ωから∞Ωまで変化させても回路電流はI0一定で変化せず、端子電圧は負荷抵抗Rの値に比例して変化します。ここまでは教科書に書かれている内容です。ちなみに定電流源の内部抵抗が∞Ωである理由は外部から電圧印加された時に電流値が変化してはいけないからです。これは「定電圧源に電流を流したときに端子電圧が変化してはいけないから、内部抵抗を0Ωと定義する」事の裏返しなのですが、直感的にわかりにくいので単に「定電圧源の裏返し」としか説明されない傾向にあります。

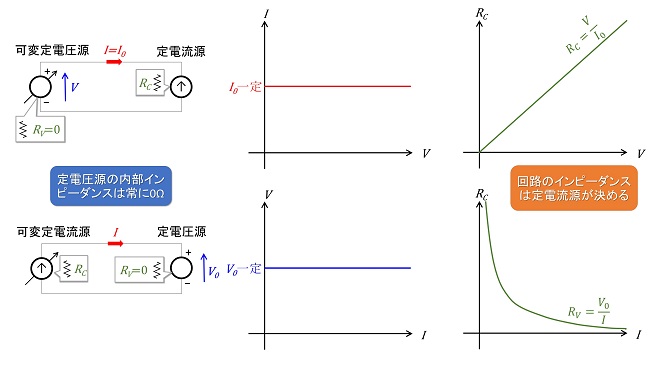
次に、定電圧源の負荷に定電流源を接続した場合、あるいは定電流源の負荷に定電圧源を接続した場合を考えます。ちょっと言葉遊びみたいになってしまいましたが、図2に示すように両者は本質的に同一の回路であり、定電圧源、定電流源のどちらを電源と見なし、どちらを負荷と見なすかと言うことになります。

図2 理想定電圧源と理想定電流源を接続した場合

「電源の負荷に電源を接続する?」と疑問を持たれる方もおられると思いますが、トランジスタのコレクタを定電圧電源に接続した場合の等価回路等は、これに準じた接続になります。

図2に示すように、定電圧源に定電流源を接続すると回路の電圧は定電圧源が定め、回路電流は定電流源が定める事になります。先程は定電圧源の内部インピーダンスRVは0Ω、定電流源のインピーダンスRCは∞Ωと定義されていると述べましたが、定電圧源に定電流源を接続した状態では、実質的に回路のインピーダンスは回路電圧と回路電流の比として定義されます。つまり、定電流源の内部インピーダンスRCは∞Ωといいつつ、回路に組み込まれて端子電圧が規定された時点で有限の値(V0/I0)に定まります。

第9話に登場した差動増幅回路は定電流源のこのような性質を利用してトランジスタ差動対のエミッタ電流を一定に保ちました。

2.実際の定電流源(定電流回路)

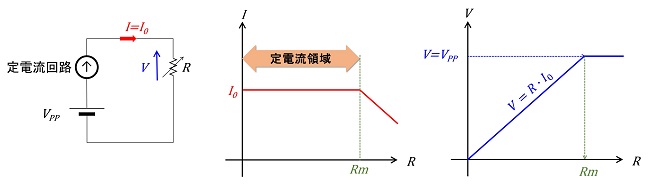
バッテリーに代表されるように、我々が手にすることができる電源は基本的に「電圧源」です^※。従って、電子回路上で定電流源が必要になるときは図3に示すように、電圧源に定電流回路を組み合わせて実現します。定電流回路とは、外部から(電圧源から)電力供給を受けて、負荷抵抗の大きさにかかわらず一定電流を供給するように動作する回路の事です。

図3 実際の定電流源

この結果、我々が電子回路の中で実現する定電流源は自身の電源電圧VPPを超えて端子電圧を上昇させる事ができず、定電流特性を示す出力電圧領域が限定されています。

※ご指摘を受けるかもしれないので補足します。
理想定電流源というのは定電圧源の完全な裏返しになるので、端子間を開放にする事ができません(端子電圧が∞に上昇します）。電圧源は端子を開放すると電流が0になって所謂「OFF」状態ですが、電流源の場合の「OFF」状態は端子間電圧を0Vに保つ必要があるため、両端子を短絡せねばなりません。「電源」として見た場合、電流源とは恐ろしく扱いにくい電源であり、恐らくこのような取り扱いを行う電源は我々の身近には存在しないのではないかと思っています。

(1) 定電流特性を実現する仕組み
「Mr. Smithとインピーダンスマッチングの話」の第22話「(1)トランジスタの動作のお復習い」の項で結論のみ解説したのですが、能動領域におけるトランジスタのコレクタ電流ICは、コレクタ電圧VCEの関数にはならず、ベース電流IBのhFE倍になります。この特性はFETでも同様で、能動領域においてはドレイン電流IDが、ドレイン電圧VDSの関数にはならず、ゲート電圧VGのgm倍となります。

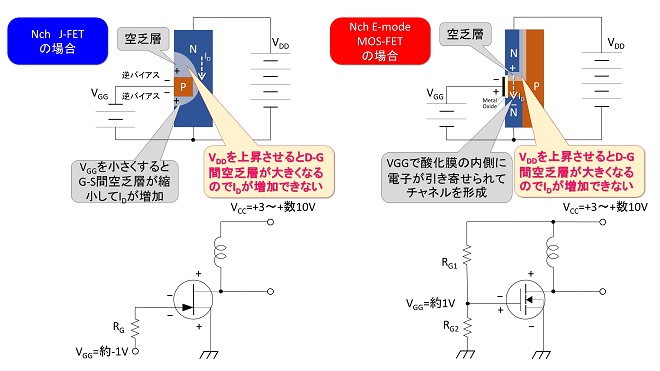
では何故このような特性になるのでしょうか。図4,5は「Mr. Smithとインピーダンスマッチングの話」の第18話の図2と図5を再掲して説明を加えたものです。同話では高周波増幅回路でS12が大きくなる原因「コレクタ帰還容量COB」、「逆伝達キャパシタンスCRSS」の発生理由としてコレクタ－ベース間(ドレイン－ゲート間)が逆バイアスであり、ここに空乏層が生じるためと解説しています。実はこの空乏層がコレクタ電流IC(ドレイン電流ID)の増加を抑える働きをしています。ベース電流IB(ゲート電圧VG)一定でコレクタ電圧VCE(ドレイン電圧VDS)を上昇させると、本来ならIC(ID)は増加するところですが、この空乏層が大きくなって相殺してしまい、能動領域においてはIC(ID)がVCE(VDS)の関数にならないのです。

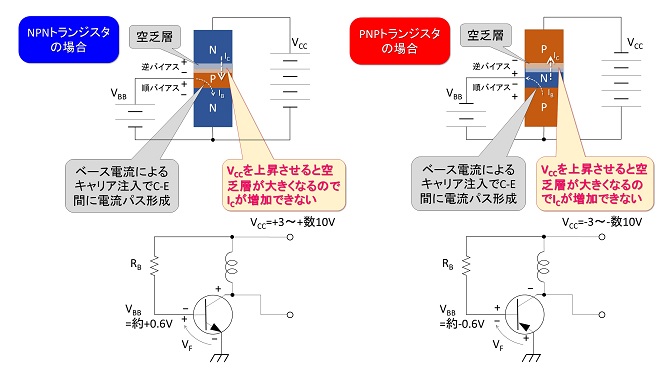
図4 定電流特性が生じるメカニズム(バイポーラトランジスタ)

図5 定電流特性が生じるメカニズム(FET)

この結果、バイポーラトランジスタのコレクタ、電界効果トランジスタのドレインは、共に能動領域では定電流特性を示すのです。

(2) 定電流回路
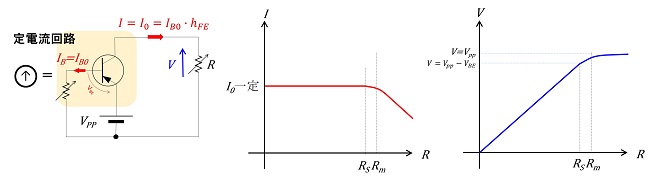
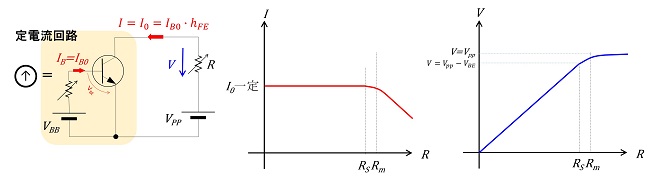
ということで、図3に示した定電流源を実際にトランジスタで実現しようとすると、図6、または図7に示す回路になります。何れもコレクタから出力を取り出しますが、負荷に電流を供給する動作が必要な場合はPNPトランジスタ(図6)、負荷電流を定電流で引き込む場合はNPNトランジスタ(図7)を使用する事になります。

図6 原理的な定電流回路(ソース(吐き出し)型)

図7 原理的な定電流回路(シンク(吸い込み)型)

これらの回路はコレクタ－ベース間電圧VCBが逆バイアスを維持している間は定電流回路として働き、ICはコレクタ－エミッタ間電圧VCEに関係なくIBの大きさのみで決定されます。コレクタ－ベース間電圧VCBが順バイアスになると、トランジスタは所謂「ON状態」となるため、回路電流ICはVPPとRの値のみで決定される事になります。

3. カレントミラー回路

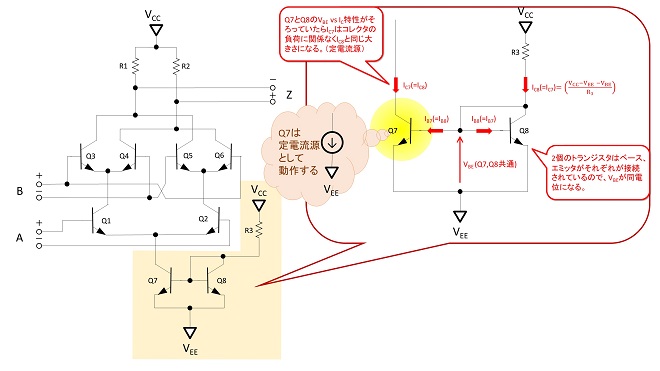
ようやく本題に辿り着きました。第9話で解説したとおり、カレントミラー回路はモノリシックIC上で多用される定電流回路です。図8は第9話の冒頭で触れたギルバートセルの全体回路ですが、この回路を構成する中のQ7,Q8とR3の部分がカレントミラー回路になります。

図8 カレントミラー回路(シンク(吸い込み)型)

この回路では、その名の通りQ7のコレクタ電流が「鏡に映したように」Q8のコレクタ電流と等しくなります。図8の吹き出し部分がカレントミラー回路のみ抜粋したものになります。第9話で解説した差動増幅回路の時と同様、話を簡単にする為にQ7,Q8のhFEは充分に大きくIB7,IB8はIC7,IC8に対して無視できると仮定します。このときQ8のコレクタ電流IC8はQ8のコレクタ－エミッタ間電圧をVCE8とすると、(式3-1)で与えられます。

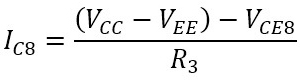
(式3-1)

Q8はベースがコレクタと接続されているので、どれだけベース電流が流れても、コレクタ電圧VCEがベース電圧VBE以下にはならず、飽和領域に入ることはできません。従ってVCEは能動領域が維持される最小電圧まで下がった状態になります。
すなわち

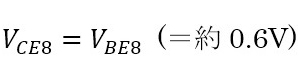
(式3-2)

となるので、(式3-1)は、

(式3-3)

となって、最終的にIC8はR3の大きさで設定することが可能です。

次にQ7を見ると、Q7はベース、エミッタがそれぞれQ8のベース、エミッタと接続されているので、

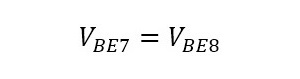
(式3-4)

となります。差動増幅回路の場合と同様、Q7とQ8が「全く同じ」特性で動作する場合は、

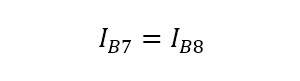
(式3-5)

も同時に成立し、さらにQ7とQ8のhFEも等しいので、VCE8≧VBE8であれば

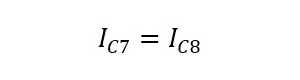
(式3-6)

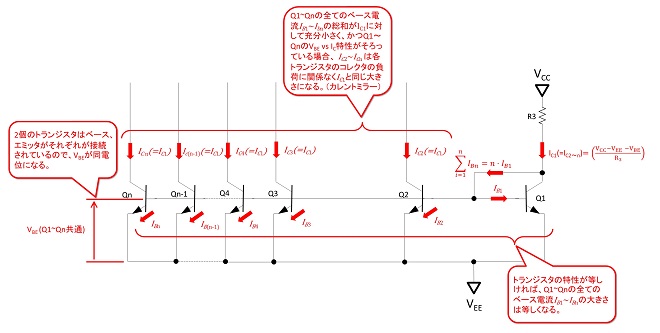
となります。つまりR3の値で設定した電流値(IC8)がQ7のコレクタ電流IC7に(鏡に映したように）反映されることになります。この時Q7はQ8と同様、能動領域にあるので、コレクタ電圧がIC7の大きさに影響しないのは2節で解説した通りです。この回路は図9に示すようにペアにするトランジスタの数を増やすことによって、複数の回路に同じ大きさの電流源を提供する事が可能です。

図9 複数の電流源を構成するカレントミラー回路

図9においてn個のトランジスタのベース電流の総和がIC1より充分に小さいと見なす事ができれば、Q2～Qnのコレクタ電流IC2～ICnは全てQ1のコレクタ電流IC1と等しくなります。また図8，図9では吸い込み(定電流で電流をトランジスタに流し込む)タイプの回路を説明しましたが、PNPトランジスタで構成した場合はソース型(トランジスタから定電流で電流を流し出す)の回路を構成することができます。

4. 第10話のまとめ

第10話は差動増幅回路のエミッタ部分に挿入されて、同相信号(＋入力と－入力に電位差が生じない電圧変化)を出力に伝えない働きをする「定電流回路」の動作について解説しました。以下、第10話の要約です。

1. 理想の定電流源とは負荷抵抗の値に関係なく一定の電流を保とうとする電源である。
2. 実際の定電流源は定電圧源に定電流回路を組み合わせることで実現される。
3. 定電流回路とは端子電圧に応じて端子間抵抗(内部インピーダンス)が変化する回路である。
4. 定電流回路はトランジスタのコレクタ電流がコレクタ電圧の値には影響されず、ベース電流の関数になる特性を利用して実現している。
5. カレントミラー回路はベース、エミッタをそれぞれ共通接続した複数のトランジスタで構成した定電流回路群であり、全てのトランジスタのベース－エミッタ間電圧が等しいときに、全てのトランジスタのコレクタ電流が等しくなる事を利用した回路である。
6. カレントミラー回路は差動増幅回路と同様、回路を構成するトランジスタ全てが同一特性である事が必須であるため、ディスクリート回路では使用されず、もっぱらモノリシックICのチップ上で実現される回路です。

次回はギルバートセルによる乗算動作の解説です。