今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第24話 同一周波数のサイン波の掛け算と周波数の話(3)
2024年3月1日掲載
第23話ではトランジスタ周波数逓倍回路の動作原理について解説し、実際の設計事例として出力回路設計とバイアスの最適化設計まで実施しました。第24話では第23話から引き続き、周波数逓倍回路の入力回路の設計について解説します。
1. トランジスタ周波数逓倍器の設計(第23話のおさらい)
第23話では、2SC4276を題材とし、400MHzのサイン波を入力して1200MHzを出力するトランジスタ逓倍器を設計することとして、下記手順のうち、①~④まで作業をすすめました。
① 出力フィルタ(1200MHzバンドパスフィルタ)の設計
② トランジスタの負荷線(負荷インピーダンス値)の決定
③ 出力インピーダンス変換回路の設計
④ 動作点(バイアス電流IBq)の決定
⑤ 入力インピーダンスの見積もり
⑥ 入力整合回路の設計
⑦ 入力整合回路の最適化
第24話は⑤から始めます。
⑤入力インピーダンスの見積もり
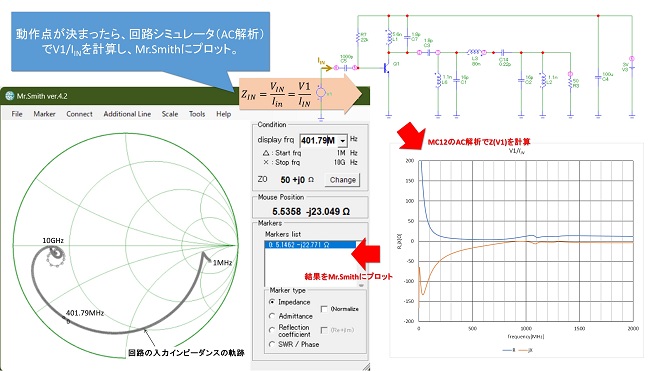
第23話で設計した回路の入力インピーダンスは回路シミュレータで実際に計算してみるのが手っ取り早くて簡単です。具体的にはインピーダンスを求めたい回路ノードの電圧と電流の比を計算します。ここでは前回に引き続きMC12※1のAC解析機能を使用して電源周波数対インピーダンス特性を計算します。計算結果はcsv(カンマ区切りテキストファイル)に出力し、Excelで加工してMr. Smithに読み込ませて表示させました※2。図1に計算結果を示します。操作方法の詳細は各アプリケーションのヘルプファイル等を参照してください。
図1に示すとおり、この回路の入力インピーダンスは、回路ノード⑥の電圧を回路ノード⑥に流れ込む電流IINで割った値となります。ここで、回路ノード⑥の電圧はAC解析のために接続した定電圧源V1の端子電圧になります。MC12ではV1のインピーダンスZ(V1)として計算することが可能です。回路の入力インピーダンスは容量性を示しており、400MHz付近では5Ω程度の小さい値になっていることがわかります。
⑥入力整合回路の設計
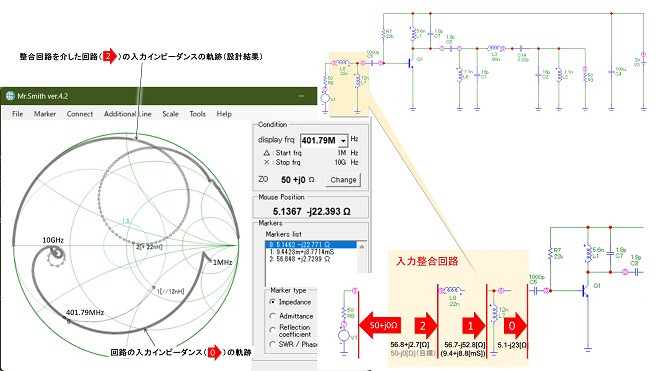
この回路の400MHzにおける入力インピーダンスは、図1のMr. SmithのMarkers listに表示されている通り、5.1-j22.8[Ω]です。入力整合回路なので、電源インピーダンスは50Ω、負荷インピーダンスが5.1-j22.8[Ω]の関係です。インピーダンス整合回路の考え方(負荷インピーダンスを電源の複素共役インピーダンスに変換する)に当てはめると、5.1-j22.8[Ω]を50Ωに変換する回路の設計になります。設計は出力Mr. Smith※2を用いて行いました。インピーダンス変換回路の具体的な設計方法は筆者の別連載「Mr. Smithとインピーダンスマッチングの話」で詳しく述べていますので、そちらを参照してください。設計結果を図2に示します。また図1と同じ手法で整合回路の入り口から周波数逓倍回路を見たときのインピーダンス軌跡をMC12のAC解析で計算した結果を図3に示します。図2、図3共に机上計算の結果なので当然ですが、両者はよく一致します。
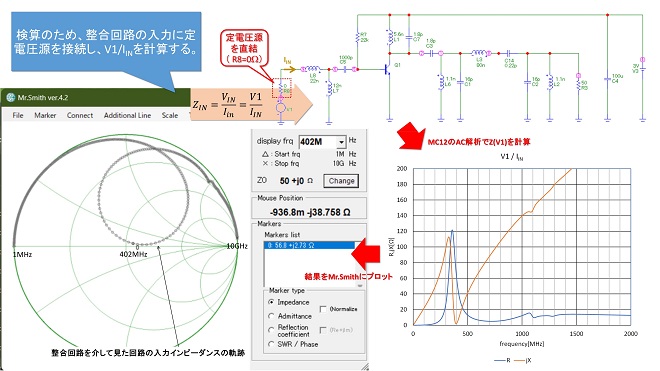
図3 設計した入力整合回路を介して周波数逓倍回路を見たときのインピーダンス軌跡
⑦入力整合回路の最適化
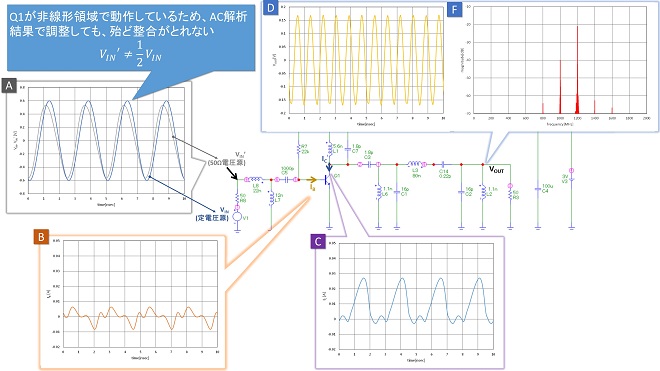
以上で周波数逓倍回路の設計を一通り完了したので、実際に内部インピーダンス50Ωの電源を接続して全体動作を確認することにします。図3の解析で0Ωに設定したR8を50Ωに戻して、第23話2章④と同様、MC12でトランジェント解析を行います。結果を図4に示します。
本来の目論見であれば、⑤項での検討結果から整合前の入力インピーダンスが約5Ω、これに整合回路を介して50Ωの電源から電力を供給するので、図4の回路図のノード⑥における振幅を第23話の図6のノード⑥と同等にするためには、(式1-1)から、約3倍強の電圧振幅が必要になります。
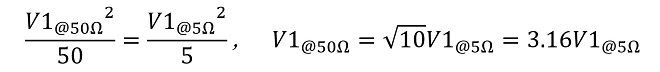
(式1-1)
第23話の図6の信号源電圧(V1)が0.3V、従って図4の回路図のノード⑨において、0.95V程度の電圧振幅を与えれば逓倍出力は同程度になることが期待できます。これに対して図4の回路図のノード⑨の電圧振幅は約0.5Vになっているので、出力の振幅は第23話の図6の出力スペクトルに対して6dB弱低下すると予想されます。しかし実際には図4右上Fのグラフでは逓倍出力である1200MHzのスペクトルのレベルは第23話の図6の同図の値より10dB程度低下しています。つまり、定電圧電源で励振したときと比較して回路の逓倍効率が低下しています。この理由としては、入力インピーダンス整合がとれていないことが考えられます。図4の左側の入力電圧のグラフAは定電圧源VIN(V1: ノード⑦)と50Ω電源の出力電圧VIN’(ノード⑨)の両方をプロットしていますが、逓倍回路の入力インピーダンスと電源インピーダンスが完全整合していれば、
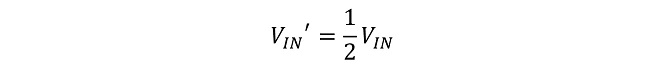
(式1-2)
が成立するところですが、VIN’がそこまで下がっていない様子がわかります。⑥項でVSWR<1.5に整合させたはずなのにどういうことなのでしょうか。
これは周波数逓倍回路が非線形動作をすることが原因です。⑤項で入力インピーダンスを計算したときは、MC12のAC解析モードを使用しました。AC解析モードは回路の特性を周波数領域で計算します。ある周波数の信号を入力したとき、AC解析では、その信号はほかの周波数に変換されることなく出力される・・・ すなわち非線形動作しない事を前提に計算しています。従って回路に流れ込む電流IINと入力電圧VINの比は常に一定です。一方で、周波数逓倍回路においては入力信号のべき乗出力を得るためトランジスタを大振幅で非線形動作させます。この結果IINと入力電圧VINの比は入力電圧VINの大きさで変化し、図4の波形Bに示すとおり、トランジスタのベースに流れ込む電流IBの波形は回路の入力電圧VINの波形と形が異なってしまいます。
これは時間軸上で見たときに瞬時のインピーダンスが変化していることを意味しており、AC解析の結果と実際の入力インピーダンスは一致しない事になります。周波数逓倍回路においては、入力信号の1周期の間にインピーダンスが変化してしまうため、周波数領域でのインピーダンスは事実上定義できないのです。このため定電圧駆動と同等のパフォーマンスに近づけるためには、線形動作させた時の条件で設計した入力整合回路をトリミングして最適化する必要があります。図5に整合回路の諸元を調整して最適化を実施した結果を示します。
最適化は、出力のスペクトル(図5のグラフF)を見ながら1200MHzのスペクトルのレベルが最大、その他のスペクトルのレベルが最小になるように、入力整合回路の各諸元を少しずつ振るという手順で実施しました。図4のグラフFと比較して、1200MHzのスペクトルが約6dB上昇し、200MHz離れのスペクトルは20dB以上低下しています。ベース電流の波形(グラフB)が変化していることが、その理由ですが、振幅はあまり変化しておらず、さらに入力電圧波形(グラフA)は図5の方が反射量が大きくなっていることを示しているので、入力整合を改善したというよりは、トランジスタから見た信号源インピーダンスを変化させて反射位相を変えることにより不要スペクトルを抑圧(相殺)したと考えた方がよいでしょう。つまりLNAの設計で行う「NFマッチ」※3と同様、「入力整合をとった」のではなく「信号源インピーダンスの最適化を行った」と捉えるのが正しいと考えます。
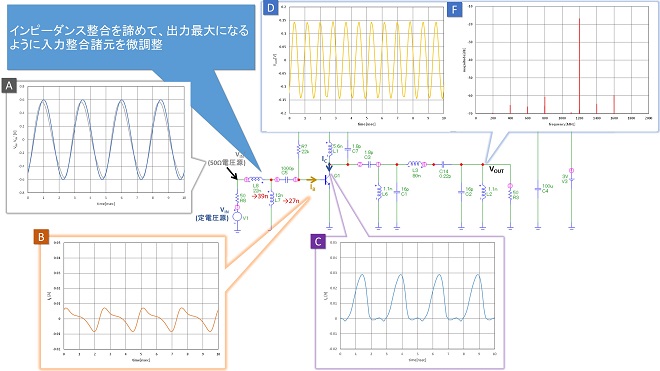
図5 整合回路の諸元を調整して1200MHzスペクトルを最大にする
2. 第24話のまとめ
第24話ではトランジスタ周波数逓倍回路の入力整合回路の設計について解説しました。以下、第24話の要点です。
- (1)トランジスタ回路の入力インピーダンスは回路シミュレータのAC解析で入力に定電圧電源を接続して流れる電流を計算することにより導出できる。
- (2)ただし、非線形動作を行う回路においては、入力電圧に応じて回路(トランジスタなど非線形動作をしている素子)のインピーダンスが変化するため、インピーダンス整合をとるという概念が成立しない。
- (3)周波数逓倍回路における入力整合回路の役割は、インピーダンス整合ではなく信号源インピーダンスを最適化することにある。
- (4)信号源インピーダンスの最適化とは、トランジスタの入力(B-E間)で発生する高調波の反射位相を調整して不要波を相殺させることで逓倍効率を改善することである。
周波数逓倍回路のほか、ミキサ回路のLO端子など、非線形動作を行う回路においては、入出力ともにインピーダンスが定義できません。このため整合回路の目的は「インピーダンスマッチング」ではなく「信号源インピーダンス、または負荷インピーダンスの最適化」となります。
第24話までは「同一周波数のかけ算」を行う回路について解説してきました。第25話以降では変復調等をテーマにするつもりですが、その前段階としてマイナスの周波数、複素周波数の概念について解説します。
- ※1 第5話でご紹介した、回路シミュレータMicro Capの無料ダウンロードサイトは2023年2月で閉鎖されましたが、以下URLでバックアップが公開されています
Spectrum Software - Micro-Cap 12. Analog simulation, mixed mode simulation, and digital simulation software. SPICE and PSpice® compatible circuit simulator. (archive.org)
MC12の日本語版のダウンロードは2024/1現在、下記URL等から可能なようです
Micro-Cap 12 Full CD Version 12.2.0.5 (Japanese) : Spectrum Software : Free Download, Borrow, and Streaming : Internet Archive - ※2 MC12のAC解析結果をMr. Smithに表示させる手順は以下を参考にして下さい。
①MC12のAC解析ウィンドウで解析実行後、ACメニューから「リミット」を選択
②表示されたリミットウィンドウのプロパティボタンを選択してAC解析のプロパティウインドウを開く
③曲線の保存タブを選択してインピーダンス曲線を選択し、形式を16桁科学、ファイル様式を.CSVに設定して計算結果を保存
④保存したCSVファイルをExcelで開き、Mr. SmithのR+jXマーカファイルフォーマットに合うように編集する。
なおMr. SmithのR+jXマーカファイルフォーマットは、Mr. Smithのヘルプファイルを「Explanation of each part」→「Main menus」→「File(ALT + F) menus」→「The format of R+jX Marker file」と辿っていただくと記載されています。
⑤Mr. Smithの「File」メニューからOpen→Marker file→R+jXの順に選択し、表示されたダイアログから④で作成したファイルを読み込みます。
⑥なおMr. Smithは下記URLからダウンロードできます。
https://www.vector.co.jp/soft/winnt/business/se521255.html - ※3 「Mr. Smithとインピーダンスマッチングの話」第28話を参照
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)