今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第30話 三角関数のかけ算と無線工学の切っても切れない深い縁
2024年9月2日掲載
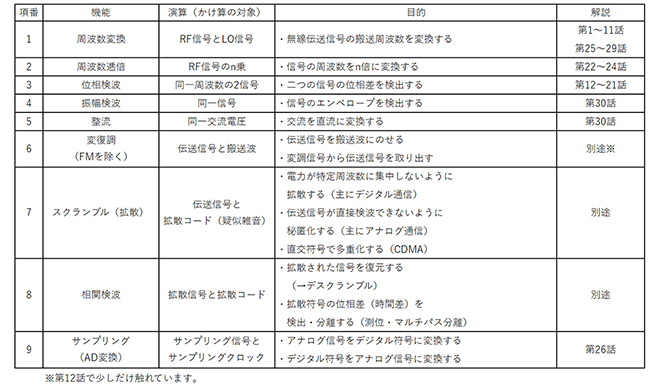
「今更人にはきけない話」の最初のテーマとして、2年6ヶ月にわたり「かけ算」、特にサイン波のかけ算をテーマにした話を書き綴ってきました。このテーマで完全にネタ切れかというと、必ずしもそうではないのですが、無線工学で登場するコアの部分は語ったように感じるのと、読者の皆さんもそろそろ飽きてこられたのではないかと思い、いったんエピローグにしようと思います。表1は第1話に掲載した「無線通信機で使われるかけ算」の一覧です。最右列に本連載の第何話で取り扱ったかを追記しました。
この中で項番6~8は帯域のある信号(サイン波の集まり)と搬送波(サイン波)のかけ算なので、項番1の応用問題になります。ただし変復調に関わる技術領域なので、別の機会に変復調のテーマ枠で解説したいと考えます。なお第12話の4章で少しだけ復調(同期検波)について触れています。項番4と5は本質的に同一周波数のかけ算になりますが、世間一般ではサイン波のかけ算とは捉えられていません。本話で簡単に触れたいと考えます。以下、【テーマ1】の振り返りとして、本表各項について要約しておきます。
1. 周波数変換とミキサ回路(周波数の異なるサイン波のかけ算)
「周波数変換」はサイン波のかけ算の基本的な用途であり、本テーマにおいて、最も多くの回で触れた話題です。全体としては「周波数変換(サイン波のかけ算)の基礎」「各種ミキサ回路の原理と設計」「直交ミキサ」の3つのサブテーマで解説しました。
1.1 周波数変換(サイン波のかけ算)の基礎
「周波数変換」をテーマにして、周波数の異なるサイン波同士のかけ算について解説しました。電子工学や無線工学の教科書では、「入出力伝達特性が非線形のデバイスで入力信号を歪ませることでかけ算できる」というような解説に留まっていることが多く、イメージが湧かないまま暗記した方も多いのではないかと思いましたので、Excelを用いた波形計算を用いて詳しく解説しました。ここでの要点は以下の通りです。
- (1) 2つのサイン波がかけ算されると、時間軸上の波形は三角関数の加法定理が示す和周波成分と差周波成分を足し合わせた波形になる。この時、両者の周波数が離れていると、高い周波数側の波形が低い周波数側の波形で揺らいだ波形になり、両者の周波数が近いと、ビート(うなり)波形になる。→第1話
- (2) 2つのサイン波を混合(足し算)しても(1)の波形が得られるだけで和周波成分や差周波成分は得られない。混合した波形を非線形デバイスに入力することで、乗算された成分が得られる。→第2話
- (3) 非線形デバイスとは、印加された電圧や電流(要するに入力信号)の大きさに応じて、利得やインピーダンスが変化するデバイスの事である。非線形デバイスに入力された2つのスペクトルAとBにおいて、Aの振幅の大きさでBの出力振幅が変化する結果、出力にはA×Bの成分が生じるというのがアナログ回路におけるかけ算の基本原理である。→第2話
- (4) 送受信機の周波数変換回路において、上記BはB=B1+B2+B3・・・ (B1,B2,B3・・・ Bnはそれぞれ異なる周波数のスペクトル)である。Bの成分相互がかけ算されないようにするため、上記AとBの振幅差をA≫Bの関係に保つ。これによりBがある振幅になるまではBとA×Bで生成される各スペクトル成分の間に線形性が保たれる。→第3話~第4話
1.2 各種ミキサ回路の原理と設計
第5話からは実際のミキサ回路(アナログ乗算回路)について、回路シミュレータを用いて解説しました。題材にしたのは、トランジスタミキサ(第5話~第6話)、ダブルバランスドミキサ(ダイオードミキサ) (第7話~第8話)、差動増幅回路の動作原理(第9話~第10話)と差動増幅回路を用いた乗算回路(ギルバートセル乗算器: 第11話)でした。ここでは非線形動作をする回路をシミュレートするテクニックとして、トランジェント特性シミュレーションとFFT解析を組み合わせる方法を紹介しました。かなり初歩的、かつ力尽くのシミュレーションではありますが、昨今のパソコンは計算能力、メモリ容量とも進化していますので、この方法でもある程度の回路動作をシミュレートすることが可能であることを示しました。ここでは1.1(4)で解説した条件すなわち、帯域幅のある信号Bの各スペクトル同士はかけ算されずに信号Aとだけかけ算されるための動作条件を実際の回路で理解していただくことがもう一つの狙いでした。具体的に信号AはLO信号、信号BはRF(またはIF,AF)信号に該当するわけですが、いずれのミキサ回路においてもトランジスタを非線形ドライブしたり、ダイオードをスイッチさせるのはLO信号の役割で、その非線形ドライブされたデバイスをRF信号が通過する結果、RF信号の各項(スペクトル)にLO信号がかけ算されるということを解説しました。
また、話のついでで解説した感が若干ありますが、第9話で扱った差動増幅の基礎や、第10話の定電流回路とカレントミラー回路はモノリシックアナログ集積回路においては避けて通れない基本回路といえます。
1.3 直交ミキサ
本テーマの最後で再度周波数変換に話を戻して、交流ベクトル空間について解説しました。三角関数の拡張概念であるマイナスの周波数と交流ベクトル空間について解説し、マイナスの周波数を観測する仕組みが直交検波回路であること、ならびにかけ算で周波数変換を行うと、必ず発生するイメージ周波数について解説しました。ここでの要点は以下の通りです。
- (1) RF信号とLO信号をかけ算することで低い周波数(IFまたはAF)信号を出力するダウンコンバータには、同一の出力周波数に変換される入力周波数が必ず2つ存在し、目的信号の周波数と異なる方をイメージ周波数と呼ぶ。→第29話
- (2) イメージ周波数はスーパヘテロダイン方式の受信機において、受信特性を劣化させる要因であり、ダウンコンバータの入力側でしっかり減衰させる必要がある。→第29話
- (3) マイナスの周波数とは、交流ベクトル空間において、位相ベクトルが時計方向に回転している交流を示す。→第25話
- (4) RF信号の交流ベクトル空間での挙動は、直交ミキサ、すなわち直交関係にある2つのLO信号(cos波とsin波)とそれぞれかけ算することにより、ベクトル空間の実軸(I信号)、虚軸(Q信号)として観測することができる。→第26話~第27話
- (5) 直交ミキサの出力周波数の±はLO信号の周波数(基準)と入力周波数の大小関係で決まる。
+の周波数と-の周波数で虚軸(Q信号)の位相が180°反転する。→第26話~第27話 - (6) 直交ミキサを用いたダウンコンバータにおいて、ベースバンド出力のI側、またはQ側を90°位相遅延させて合成することで、LO周波数に対してUSB側、またはLSB側の周波数成分のみダウンコンバートして出力させる事が可能(イメージリジェクションミキサ)。→第27話、第28話、第29話
- (7) ベースバンド信号(AF信号)にI、Qの2つの信号を用いて+周波数、-周波数を表現し、直交ミキサで直交LO信号とかけ算(アップコンバート)すると、和周波(USB)成分のみ、差周波(LSB)成分のみを取り出す事ができる。→第27話、第28話、第29話
2. 周波数逓倍(サイン波のべき乗)
第22話~第24話は「同一周波数のサイン波のかけ算と周波数の話」というタイトルでしたが、サイン波とサイン波のかけ算の延長として、サイン波をべき乗するとどうなるかについて解説したものでした。併せてトランジスタを使用した周波数逓倍回路の設計について、回路シミュレータを用いて解説しました。要点は以下の通りです。
- (1) サイン波の二乗は同一周波数のサイン波同士のかけ算と見なせる。出力には2倍波の成分(和周波)と直流成分(差周波)のスペクトルが得られる。→第22話
- (2) サイン波の三乗は、(1)のスペクトルにさらに同一周波数のサイン波をかけ算した結果となり、3倍波成分と1倍波成分のスペクトルが得られる。一般化すると、サイン波をn乗すると元の周波数のn倍波が得られる。→第22話
- (3) べき乗演算はダイオード(半導体PN接合)の電圧電流特性が、印加電圧の指数関数に比例することを利用して実現する。但し出力電圧を取り出すために負荷抵抗を装荷するすると非線形領域は非常に小さくなるため、出力電力が必要な場合はトランジスタを用いる。→第22話
- (4) トランジスタを周波数逓倍器として使用する場合、入出力の整合回路は共役整合を行うのではなく、所定の信号源インピーダンス、負荷抵抗が接続されたときに、トランジスタから見た信号源インピーダンス、負荷インピーダンスが所望の周波数で最適点になるようにインピーダンス変換する。→第23話~第24話
3. 位相検波(周波数が等しいサイン波のかけ算)とPLL
第12話は「同一周波数のかけ算と位相の話」と題して同一周波数のサイン波どうしをかけ算するとどうなるかについて、全般的な解説を行いました。また、第13話~第21話では位相検波器の代表用途といえるPLLの動作原理と用途について解説しました。
3.1 周波数が等しいサイン波のかけ算と位相検波器
周波数の異なるサイン波同士のかけ算は周波数変換に用いられました。一方で同一周波数のサイン波同士をかけ算すると、和周波が2倍波、差周波が直流になり、前者を取り出す回路は2項で述べた周波数逓倍、後者を取り出すのが位相検波回路となります。また、やや趣が異なりますが、変調された搬送波信号に搬送波と同一のサイン波をかけ算すると、搬送波が直流に変換されるので、変調信号を取り出す事ができる事にも触れました。要点は以下の通りです。
- (1) 同一周波数のサイン波をかけ算すると、その差周波成分は、かけ算したサイン波の位相差に相当する直流となる。→第12話
- (2) 帯域を有する信号(変調されたRF信号)に、搬送波と同一周波数のサイン波をかけ算すると、搬送波が直流に変換されて変調信号のスペクトルが出力される。これが復調回路の原理である。→第12話
- (3) 位相検波器にはJKフリップフロップ回路をベースにしたデジタル方式の位相・周波数検波回路とアナログ乗算器による位相検波器がある。前者は位相差が±180°を超えた時に、周波数差の大小関係を表示することができるが、収束点(位相差0°)付近で検波感度を失う欠点がある。一方でアナログ乗算器は収束点(位相差90°)で検波感度が最大になるが、180°を超えて検波することができない。→第15話
3.2 PLL回路
第13話~第21話では、電気信号として実在するサイン波の純度の表し方、ならびに無線通信においてサイン波の純度に関わる要素を取り扱うPLLについて解説しました。PLLは位相検波器の用途でもありますが、PLLを構成する要素技術は「位相検波」「負帰還制御」「発振回路」の3つであり、ここでは「位相検波」と「負帰還制御」について解説しました。要点は以下の通りです。
- (1) 電気信号としてのサイン波に加わる雑音には、振幅雑音・振幅オフセット・周波数変動・周波数偏差・位相雑音・位相オフセットが存在する。このうち位相雑音はサイン波の純度に直接影響し、かつ一般的なフィルタで取り除く事ができない。→第13話
- (2) PLLの役割は大きく、①サイン波に含まれる位相雑音を取り除くフィルタ機能、②サイン波の周波数精度を維持したまま別の周波数に変換する機能、③FM信号やFSK信号から音声信号や伝送テータを取り出す復調機能の3つの機能がある。→第13話
- (3) サイン波に含まれる位相雑音を取り除くためのPLLは、位相雑音レベルの低いVCO(VCXO等)を用い、ループの閉ループ通過帯域を狭くして雑音を含む入力サイン波の中心周波数に同期させる。→第14話
- (4) 入力サイン波の純度・精度を維持したまま、周波数の異なるサイン波を生成するためのPLL(シンセサイザという)は、入力回路とフィードバック回路に分周器を挿入し、入力信号よりも高い周波数で同期させる。ループの閉ループ通過帯域は広くとってVCOの位相雑音を入力信号に同期させることで抑圧する。→第14話
- (5) フィードバックループは、入力信号が出力に至り、帰還回路で入力に戻ってくるまでの時間遅延が無視できる場合のみ正しく機能する。遅延時間が無視できずフィードバック信号の位相が入力信号に対して反転してしまう周波数を極と呼ぶ。ループフィルタの通過帯域は(3)(4)の条件から決定されるが、同時に、極の周波数でフィードバック利得が生じないように帯域制限をかける必要がある。→第16話、第17話、第18話、第19話、第20話
- (6) 二次以上のループではステップ入力に対して過度応答が発生する。過度応答の大きさと振動周期は減衰定数ζと固有角周波数ωnで表される。→第21話
- (7) PLLは原理的に二次以上の次数のループとなる。一次ループは定常状態において、ループ利得に応じた同期(追従)誤差が残り、二次以上のループでは定常誤差は発生しない。二次ループではランプ入力に対して追従誤差が発生するが三次ループではランプ入力に対して追従誤差が発生しない。→第18話、第19話、第20話
4. 整流と振幅検波
周波数が等しいサイン波のかけ算の項で、まだ解説していない整流と振幅検波について触れておきます。これらは、電子回路の教科書ではダイオードのアプリケーションとして解説されますが、見方を変えると図1、または図2に示すように自身と位相の揃った矩形波をかけ算していると考える事ができます。
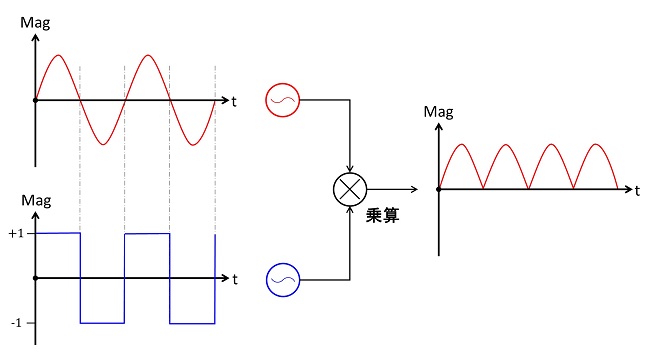
図1 全波整流をかけ算イメージで表現
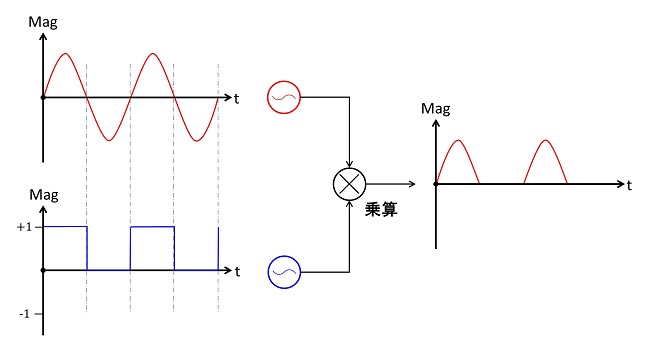
図2 半波整流をかけ算イメージで表現
従って、整流回路の出力には、(矩形波とかけ算するので)入力周波数の整数倍の成分と直流成分が出力されます。(プラス側にオフセットされるのが直流成分) →第12話の1項参照。
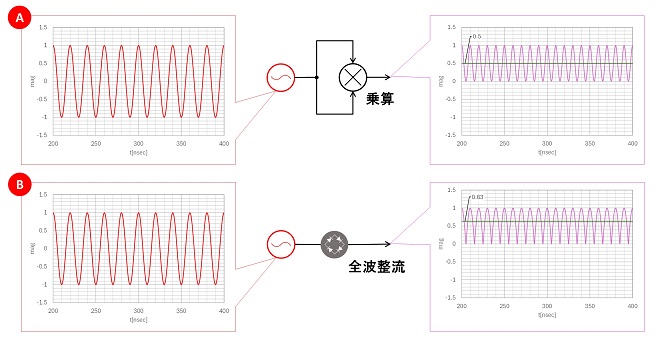
自信号を2乗したときと、ダイオードで整流したときの違いは、DC成分の大きさに表れます。自信号を2乗したときは、2倍波とDCしかスペクトルは存在しないので、図3のAに示すようにDC成分の大きさは0.5となりますが、全波整流したときはn倍波のスペクトルが含まれる波形が0V以上にオフセットされるので、DC成分は0.5よりも大きい値になります。見方を変えるとコサインの2乗の場合はオフセットコサインの全周期平均なので0.5、全波整流の場合はコサインのプラス側1/2周期の平均値になるので約0.63になります。
もっとも、整流回路や検波回路の場合は、後段に平滑回路を接続するので、出力されるDC電圧は包絡線電圧に等しくなります。平滑回路は一種のLPFと考えて間違いではありませんが、意図的にインピーダンス整合を行わないLPFであり、基本的にフィルタの映像インピーダンスよりも十分に低い信号源(整流回路)インピーダンスと十分に高い負荷インピーダンスが接続されます。この結果高調波成分を阻止した残りを取り出すのではなく、常に入力波形の包絡線(極端な場合は最大値)が出力されることになります。
5. サンプリング
表1の最後の項目「サンプリング」とは、連続的に変化するアナログ量を周期的に量子化された離散値に変換する操作、いわゆるAD変換の事です。AD変換においては、振幅の量子化(離散値化)に目が奪われがちですが、実際には振幅軸方向と時間軸方向のそれぞれに対して離散値化が行われます。このうち「かけ算」処理になるのが時間軸方向であることを第26話で解説しました。時間軸方向の離散値化はアナログ信号にサンプリングクロックをかけ算することで実現しており、本質的に周波数変換と等しい処理です。
6. テーマ1のまとめ
サイン波のかけ算をテーマにして、そこから派生する様々な話題を取り扱ってきた2年半でした。少々まとまりのない連載になった感がありますが、「非線形回路の動作原理と設計法」「PLLの応用と設計法」「直交ミキサの基礎」の三つが大きなテーマでした。これらは何れも無線通信機を理解し設計する上で避けて通れない要素技術です。高周波回路シミュレータとベクトルネットワークアナライザが廉価になり、中小の会社や大学の研究室にも普及し始めたのが、今から約30数年前。この頃から、Sパラメータを駆使できる「高周波エンジニア」が増えてきましたが、この世代のエンジニアには非線形回路が不得意な人が多く、無線通信機をまるごと設計できるエンジニアは少数だというのが、私の個人的な所見です。昨今、この領域がIC化され始めており、高周波回路の知識はチップセットを使いこなす程度あれば仕事ができるようになってきましたが、三角関数のかけ算と無線工学は、切っても切れない深い縁で結ばれており、避けては通れない技術領域です。本連載が、皆様が無線通信機の理解を深める上で少しでも参考になれば幸いです。
7. テーマ2について
テーマ2は「デシベルと無線工学」と題して、送信機・受信機の性能がどのように決まるのか解説したいと考えます。テーマ1では話を簡単にするため、非線形動作に伴う三次歪みや、サイン波の位相雑音が具体的に無線機の性能にどのような影響を与えるのか、等については割愛しましたが、テーマ2では信号の劣化要因として解説したいと考えます。現在想定している話題は以下の通りです。引き続きご愛読いただけますようよろしくお願いいたします。
(1) デシベルの基礎
・そもそもdBとは何の単位?
・dBmとdBµVの関係、10logか20logか?
・0dBmは何V?
(2) シャノンの定理
・通信が成立するかしないかはどのように決まるのか
・信号劣化とは何?
(3) 無線機の床と天井のはなし
・受信機の感度はどうやって決まるのか?
・HF受信機の初段はNFよりも飽和電力ってどういう意味?
・SINADと誤り率
等々、現在検討中です。リクエストがあれば月刊FB NEWS編集部までお知らせ下さい。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)