ジャンク堂
第20回 エクセルを使って空芯コイルのインダクタンスを計算する
電気回路計算にエクセルを用いる理由 (どうでも良い話し)
貴方が仕事であれ、趣味/遊びであれ、何らかの回路を設計する際に計算が必要になったとします。例えば、プリント基板にマイクロストリップラインを描こうとして、基板の厚みや材質からパターン幅を計算するための式が必要になったとします。
近年はそのようなときにネット上で目的に応じた計算をしてくれるサイトが数多くあるので活用されている方も多いと思います。しかし、今後も計算を繰り返して行う可能性がある場合、あなたはどうされますか?
一番簡単な方法はそのWEBサイトをブックマークしておき、次回もそこにアクセスすれば良いですね。でも私の場合、大抵は計算式を探し出して面倒でもエクセルで自分用の計算シートを作成しています。
理由は、WEBサイトで公開されているそのような計算プログラムのユーザーインターフェースが多くの場合、使いやすくないからです。1回きりであれば、良いのですが何度も計算する場合にはやはり使い易さは重要と思うからです。
もう一つ理由があります。今ほどWEB上で計算してくれるサイトが無かった時代から、自分で作ってきたそのような目的のExcelの計算シートがそれなりにあるので、手持ちの計算シートにない計算をする場合は新たに計算シートを作ると資産が増えた気分になって、少しだけ嬉しいからです。こうなると計算より計算シートを作ることが目的で本末転倒ですが。
私が電気屋の世界に入った頃は、ネットはおろか、仕事で使えるパソコンも無く(TK-80やPC-8001、Apple Ⅱはありました)全て関数電卓で計算をしていました。当時、HP(ヒューレットパッカード社)の関数電卓が電気屋の憧れでしたが、為替レートが1$=\200といったような時代でHPの関数電卓は10万円近くしたような記憶があります。
したがって、プアマン(poor man)エンジニアである新人回路技術者はカシオかシャープの関数電卓が主な武器でした。当時は丁度プログラム電卓と呼ばれる、独自のプログラムを組み込むことができる関数電卓が出て来ており、私もカシオのFX-602Pというのを買って使い倒していました。

カシオのFX-602P(Wikipediaから引用)
その後、パソコンが徐々に普及してきたころに先輩技術者からLotus 1-2-3に電気回路の式を埋め込むと非常に便利に使えることを教えてもらい感心した記憶があります。それ以後、関数電卓一本から少しずつですが仕事で頻繁に計算するものは関数電卓と併用して表計算ソフトを使用するようになり、いつの間にか関数電卓が補助の役割となりました。
このような背景からいまだにExcelで電気回路計算をしているために、最近のネットをフル活用されている方々からみると少々かったるく思われるかも知れません。
ここから本題
先日、ちょっとした理由から空芯(ソレノイド)コイルを巻くことになり、何回巻けば良いのかあたりをつけるためにExcelを立ち上げました。久しぶりにコイルのインダクタンスを計算するシートを開くと、しばらく使っていなかったものだったので、趣味の一環(?)で少し手を入れました。今回はそのソレノイドコイルの計算シートを皆さんに紹介するとともに、Excelで電気回路計算のシートを作る際の私のパターンを紹介したいと思います。
最初に言い訳から入る
いきなり、言い訳になりますが今回のソレノイドコイルの計算シート(以下、計算シート)で使っている式は、私の浅学さ故に理解できていない部分があります。特に長岡係数というものが出てきますが、こちらについてはさっぱり歯が立ちません。
また、今回この計算シートに少し手を入れたのでうっかりとバグを埋め込んだ可能性があります。このような理由から、この計算シートを使うことによって何らかの不都合を生じても、一切の責任は負えませんので、悪しからずご了承ねがいます。
また、この計算シートの計算結果は本質的に誤差を含みます。少なくとも長岡係数の参照部分で最大10%近くの誤差が出る場合があります。そのほかにも、誤差要因があると思います。ソレノイドコイルは周囲の環境(金属などの影響)を受けやすく、コイルの設置状態によってインダクタンスの変化が大きいのですが、この計算シートの誤差と合わさるとそれなりの大きな誤差となる可能性があります。他にも係数参照テーブルの都合で、コイルの直径/長さ(D/l)が10より大きくなると正しく計算できませんので、ご注意願います。
とはいうものの、通常の空芯コイルであれば、この計算シートで算出されたコイルのインダクタンスの値は、当たらずとも遠からずというレベルで十分に使えると思います。ネット上にもいくつかソレノイドコイルの計算をしてくれるページがあります。それらと比較してもピッタリと一致しなくても、それなりに近い値になっています。
それらのWEBサイトを使って計算するのも良いのですが、この計算シートは実際にコイルを巻く場合に使い易いものにしようと考えて作りましたので、良ければ皆さんも使ってみてください。
コイル計算シートの元ネタ
次に、この計算シートの元ネタ(引用元)を紹介致します。TDKのホームページにある“エレクトロニクス入門”の中にインダクタに関するページがあります。
https://www.tdk.com/ja/tech-mag/electronics_primer/1
ここに、ソレノイドコイルのインダクタンスの計算式が掲載されており、この計算シートはその計算式(下図)をエクセル上で計算するようにしたものです。
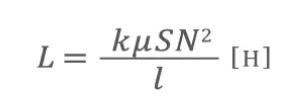
ここで、長岡係数というものが出てきます。通常のソレノイドコイルは長さが有限ですから、磁束の状態は長さが無限大の場合と異なります。そのため、それを補正するために長岡係数が存在します。つまり、無限長のコイルの場合のインダクタンスを算出する式に、長岡係数を掛けて有限長のコイルのインダクタンスを算出するようになっています。
長岡係数はD/l(直径/長さ)の比によって変化します。コイルの直径に比べてコイルの長さが長いほど値が“1”に近付きます。逆に、コイルの直径に対して長さが短い場合は係数が小さくなります。
なお、TDKのサイトにでは長岡係数は小さなグラフでしか描かれていないので、長岡係数のリストは別のところから持ってきています。
ソレノイドコイル計算シートの使い方
計算シートはこちらからダウンロードできます。なお、Excelのワークシートですが、オープンオフィスの流れを汲む、無償のLibreOfficeのCalc(表計算ソフト)でも動作するはずです。この計算シートはコイルを巻いたことがある方であれば、入力する部分をご覧頂くだけで、使えると思います。
LibreOfficeのCalcについて
近年、マイクロソフトのOfficeソフトもサブスクリプション化が推し進められているためかアップデート版が無くなり、買い換えのハードルが高くなってしまいました。以前は数年毎にアップデート版を購入していましたが、次はどうするか悩んでいます。そのため、無償のオープンオフィスへの切り替えも視野に入れて、パソコンにLibreOfficeもインストールしてあります。その中のCalcはExcelに相当するアプリです。
私の使っている範囲では、Excelで作成したシートをCalcで開いても問題無く使えています。ただしCalcで作成したシートをエクセルのファイル形式で保存しようとするとエクセル型式で保存できない内容が含まれている旨のワーニングが出ることが多々あります。
Calcは結構使える手応えはあるのですが、ユーザーインターフェース(UI)が微妙に違うために、ついつい馴れたExcelの方を立ち上げてしまいます。UIは馴れの問題でもあるので、Excelとの完全な互換性を諦めてCalcだけを使用するようにすれば問題はないと思いますが、まだその踏ん切りが付いていません。
LibreOffice: https://ja.libreoffice.org/
愚痴になりますが、オフィスに限らずサブスクリプション版は常に新しいバージョンが使えると宣伝していますが、供給側の勝手で変更されたものを次々押しつけられるのも如何なモノかと思っています。特にUIなどを大きく変えられると大抵はいい迷惑です。
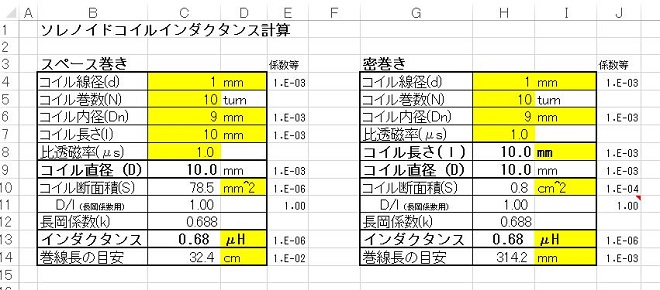
とはいうものの、一応は簡単に使い方の説明をしたいと思います。計算シートの入力の表は下記のようになっています。
このシートにはスペース巻き場合と密巻きの場合の2つの計算用の表があります。密巻きの場合はコイルの長さを自動的に計算するようになっています。
注) スペース巻きの場合、巻き線の線径と巻き数に対して、コイル長を物理的に巻くことができない値を入れてもそれなり結果が出てしまいますので注意が必要です。
黄色いセルの部分は数値入力をするか、単位をプルダウンリストから選択します。コイル長(l)については下図を参照願います。先ほどのTDKのサイトから引用しました。図は密巻きになっていますが、スペース巻きの場合は線同士の間に隙間ができます。
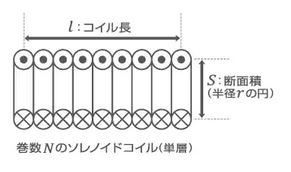
何となく不思議なのですが、インダクタンスの計算には線の太さ(線径)は使われません。使われるのはコイル長と断面積のみです。とはいうものの、線径によってコイルの最低長が決まります。密巻きのときのコイル長が最低長になります。
この計算シートでは、コイルの断面積を求めるために、コイルの内径と巻き線の線径を入力するようにしています。コイルを巻いたことがある方はご存じだと思いますが、コイルを巻くときは何らかのボビンに巻き付けます。ボビンの直径がコイルの内径になります。そのため、コイルの内径(ボビンの直径)を入力して、線径を入力することでコイルの直径を求めています。
また、ソレノイドコイルの場合1回巻きの定義が分かり難いのですが、ここでは下図のように、巻き始めと巻き終わりが丁度重なったら1回と考えています。
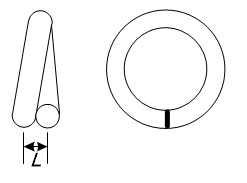
したがって、1回密巻きのコイルの長さは線径になるようにしています。
巻き線長の目安について
計算表の一番下に巻き線長の目安という欄があります。これは、コイルを巻くための線材を準備するときにあらかじめ長さを把握するために設けています。ただ、計算は極めて大雑把な計算で、密巻きのときは単にコイルの直径から円周長を求めて、巻き数倍しているだけです。スペース巻きのときは密巻きの計算結果にコイル長を足しているだけです。したがって、ここの値は極めてアバウトであることをご承知願います。
長岡係数について
Wikipediaでは長岡係数は以下のように説明されています。
長岡係数(ながおかけいすう、英語: Nagaoka coefficient)とは、無限長ソレノイドのインダクタンスを求める公式により、有限長ソレノイドのインダクタンスを求められるようにした係数であり、長岡半太郎によって提唱された。
Wikipediaの説明の下のほうに、長岡係数の算出式も記載されていますが、これをエクセルに展開するのは私にはハードルが高すぎます。したがって、あらかじめ算出された長岡係数のリスト(テーブル)を参照して計算に使用しています。ここに2つ、誤差の要因があります。
一つは、リストの数値がとびとびのために、入力したコイル形状のD/lの値とピッタリ一致しないこと。もう一つは、リストの参照に用いるVLOOKUP関数によるものです。これについては後ほど少し説明しています。
電気回路計算をエクセルシート上で行う場合に私がやっていること
ここからは私がExcelで計算シートを作る時の話しになります。コイルの計算シートでは長さやインダクタンスの単位をプルダウンリストで選択するようにしていますが、私が最近作るこの手の計算シートは全てこのようにしています。
電気回路計算の場合、ほとんどの数値に補助単位が付いています。そのため、数値に補助単位を付けて表示すると分かりやすく入力の間違いも減ります。当然、計算結果にも補助単位を選択できるようにしておきます。
ただし、テキストの補助単位を用いると計算ではややこしくなります。入力した数値に補助単位に相当する係数(指数)を値に付けて計算する必要があるからです。例えば、“3”と“pF”と数値の補助単位のセルが分かれていると、計算に用いる数値は“3”に“pF”に相当する10-12を掛ける必要があります。そのため、計算をさせるセルの記述は複雑になります。
私の場合は計算式を入力するときに間違えないように補助単位のセルの横に係数を出すようにしています。
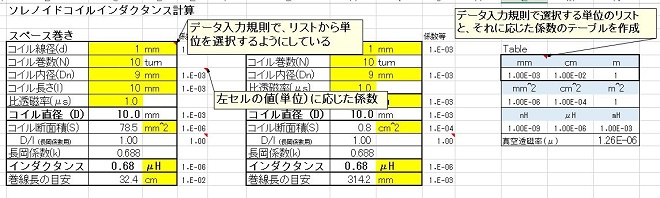
また、シートの横(あるいは下)の方に、補助単位のリストとそれに応じた係数のテーブルを作成しておきます。上記の図の右のTableと書いた部分がそれです。
注) 通常、補助単位はk(キロ)やM(メガ)の部分を言いますが、ここではkHzなど単位も含めて補助単位としています。
面倒なようですが、馴れてくるそれほど苦も無くこのようなシートを作成できます。
補助単位をプルダウンリストで選択できるようにする方法
エクセルの経験がある程度あればご存じだと思いますが、エクセルではセル毎に入力値を制限する機能があります(もちろんCalcにもあります)。それを利用してあらかじめ用意したリストから入力文字を選択するようにします。
用意するリストは横向きでも縦向きでも良いのですが、ここでは下の図のように横向きに作っています。

コイルの計算シートでは右の方にあるTableと書かれた所にリストを作成しています。この青いセルが入力範囲のリストです。ここでは、長さ、面積、インダクタンスの3種類のリストがあります。
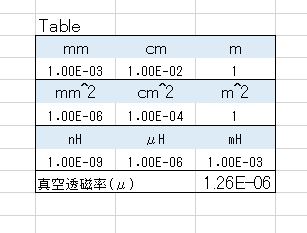
次に、その単位を表示させたいセルを指定した状態で、エクセルの一番上のタブの“データ”に移ると“データツール”の所に“データ入力の規則”という項目があります。
それをクリックすると以下のようなウィンドが現れます。
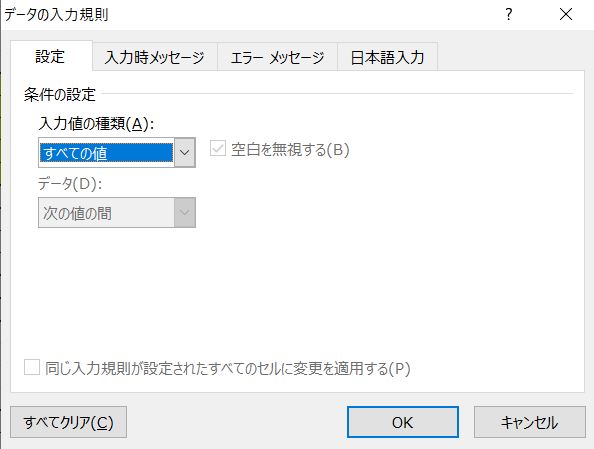
初期値は“全ての値”となっているので、このプルダウンリストから“リスト”を選択します。
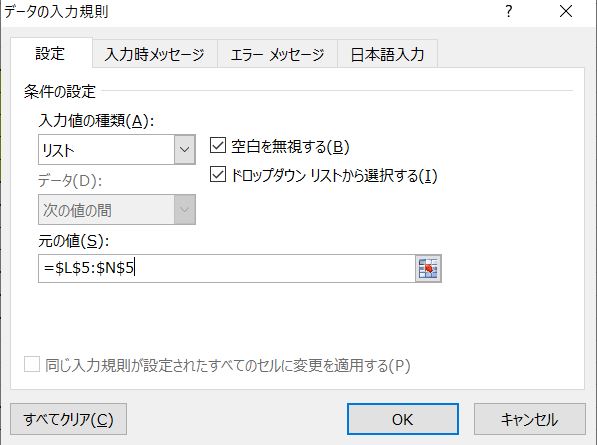
次に元の値と書かれた所に、先ほどの単位を書いたセルを指定しますが、マウスで範囲を指定することができます。そして、“OK”を押して終了します。これで、先に指定したセルにマウスを持っていくとプルダウンリストが現れて、単位が選択できるようになります。
補助単位に応じた係数を指定する。
補助単位に応じた係数の選択には“HLOOLUP”関数を使います。HLOOKUP関数はテーブル参照に相当する関数です。なお、同じ機能にVLOOKUP関数もあります。こちらは後ほど出てきます。
HLOOKUP関数には2行のリスト(テーブル)が必要で、下の図のようなリストを作成しておきます。図は先の3種のリストから長さの単位部分だけを切り出したものです。
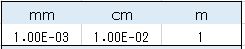
上の行はインデックスに相当し、mm/cm/mを記載します。下の行は上の行(インデックス)に応じた値を入れています。ここではmを“1”として、cmは“10-2”を、mmは“10-3”の係数を書いてあります。なお、上の行は先ほど説明した補助単位を指定する場合のリストも兼ねています。
これで、HLOOKUP関数を書いたセルには、参照しているセルに“mm”の文字があれば“1.00E-03”の値を、mの文字があれば“1”が現れます。HLOOKUP関数の書式は以下の通りです。
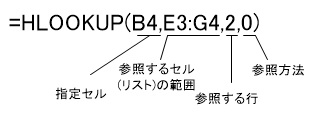
HLOOKUP関数の実際の記述の例を下に示します。
リストの上の行はインデックスに相当するデータになり、下の行が戻り値に相当します。この行の上下の関係を逆にするとエラーになります。したがって、参照する行の部分には通常は“2”を入れます。
関数の最後の数字、参照方法は少々わかりにくく、“0”(=false)を指定すると完全一致を指定し、“1”(=true)を指定すると近い値のインデックスを参照します。ここでは文字列を参照しますが、“m”と“mm”は完全一致でないと“mm”を“m”として参照してしまいます。文字列などで、同じ文字列が含まれる場合は“0”を指定します。
一方、リストが数字だけのような場合、完全一致しないことも多いため、“1”を指定して近い値のインデックスを参照するようにします。これら、エクセルの関数についてはネットなどで調べて頂いた方が分かり易いかも知れません。
計算式をセルに埋め込む
これで、計算に用いる数値の係数(補助単位に応じた指数)が準備できたのですが、セルに計算式を入れるときに少々面倒があります。
それは、入力数値に必ず係数を掛けて計算式を作成する必要があります。そのため、数式が長くなってしまいます。私は、計算式に数値と係数(指数)を一度に書いていますが、係数の横にあらかじめ入力された数値と係数を掛けた数値を入れるセルを用意しておき、計算にはそのセルを使うようにした方が間違いないと思います。
また、計算で算出された値は結果のセルの横の単位に応じた係数で割ります。具体的にはソレノイドコイルの計算シートをご覧頂ければと思います。
長岡係数の扱い
この計算シートでは長岡係数をリスト参照するようにしています。長岡係数のリストを縦に作ったので、ここではVLOOKUP関数を使います。VLOOKUP関数はHLOOKUP関数と同じで、単に参照のためのテーブルが横向きか縦向きの違いだけです。なお、今回のリストは数字のみを扱うのでVLOOKUP関数の参照方法は“1”を指定します。
VLOOKUP関数ではリストを2列で縦に作成します。長岡計数の場合1列目にD/lの値(インデックスに使う数値)を、2列目に長岡係数(数値)を入れます。また、左列の数値は小さい値から大きくなる順に並べる必要があります。
VLOOKUP(HLOOKUPも同様)関数の挙動
下の図は左の表がリスト(テーブル)になります。aの列がインデックス、bの列が値です。このテーブルではインデックスと値を同じにしています。
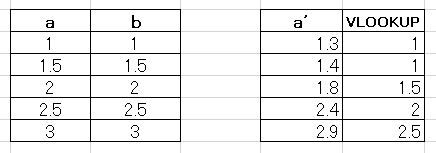
右の表はa’の値から左のリストを参照して近い値の結果をVLOOKUPの列に表示させています。a’の値は1.3のとき、1.5から値を拾うのではなく、1から値を拾っています。下の方もみて頂ければ、VLOOKUP関数の挙動がお分かり頂けると思います。四捨五入的に近い方のリストから拾ってくれれば良いのですが、そうはなっていないようです。
これも誤差を大きくする要因になっています。この誤差要因は手間を掛ければある程度回避できますが、元々誤差が大きいソレノイドコイルの計算表と思い妥協しています。
また、長岡係数のテーブルはD/lが10までのために、それを超えると正しく計算できません。直径の大きなワンターンコイルなどを作らない限り、あまり支障はないとは思いますが、上の妥協点も含めて長岡係数のテーブルを増やすか、テーブル参照をやめて係数を算出する方法に変更すれば改善ができますが、この次の宿題です。
注) 長岡係数を計算してくれるサイトが以下のところにあります。
https://keisan.casio.jp/exec/user/1225887110
また、係数のリストをExcelでグラフを描かせて、そこから近似曲線を多項式で求める方法でもある程度の精度で計算できるのではないかと思います。なお、Excelは膨大な関数を持っているので、ここで紹介した方法よりももっと適切(簡単)な方法があるかも知れません。
エクセルで計算シートを作る時に心掛けていること
私がエクセルで計算シートを作る時に心掛けていることがいくつかあります。
・VBAは使わない。
・なるべく、一つのシートの中で完結する。(複数のシートを横断しない)
・計算式などの元情報は、情報源をシートのどこかに記載しておく。
・計算式はExcelのセルの中だけでなく、数式エディタなどを使って見やすい形で記載しておく。
・関数が長くなる場合は、いくつかの関数に分けて関数を必要以上に長くしない。
・回路などが絡む場合は、回路図の画像を入れておく。
結構、面倒なことを自分に課していますが、これは永年やってきた失敗から得た教訓で、とにかく作ったシートにバグがあることを前提に、計算過程の見通しが良いようにと心掛けています。
特にVBAはもう20年以上は使っていないので、最近の様子は分からないのですが、Excelのバージョンが変わると動かなくなったり、計算の挙動が隠れてしまうので計算間違いの箇所を見つけるのに苦労があります。
ソフトウェアの世界には“3ヶ月後の自分は他人”という言葉がありますが、自分が作った物でも3ヶ月経つと何でこんなようになっているのか、理解できないのが人間です。私は1週間でダメですが、、。(苦笑)
したがって、後になっても何をしているのかが極力分かるように、間違いが見つかり易いように作成することを心掛けています。手間は掛かる様でも補助単位を表に用いるようにしていることもそのためです。
係数やテーブルも隠さないで見えるようにしているのもそのような理由からです。係数やテーブルを別シートに持っていったり、セルを隠したりすると見栄えは良くなるのですが、やはり計算間違いなどの発見や修正がやりにくくなります。見栄えは悪くてもデバッグや修正がやり易いように作ることが大切です。
計算式などの元情報も必ずシートに記載するようにしています。実は初代のソレノイドコイルの計算シートを作成したときの元情報はTDKのサイトではなく別の情報源でした。それがWEBサイトだったのか、書籍だったのか、シートに情報源を記載していなかったので分からなくなってしまいました。結局、以前に修正をしたときにTDKのサイトの情報を元情報として残すようにしたのですが、長岡係数の出所は不明のままです。
計算式を記載しておく理由もそうですが、Excelのセルに埋め込んだ式は、セル番号などで書くために元の式は一目で分かりにくいという欠点があります。以外と、式の入力ミスなども後になって気付いたりすることもあって、そのようなときに式や元情報があると修正がしやすくなります。
さて、下手なExcel講座のような内容になってしまいました。近年、Excelは技術者だけでなく、営業マンや事務職など多くのビジネスマンが使われています。そのため、世の中にはビックリするほどExcelに精通された方が多くおられます。私は使用している期間こそ長いものの使っている範囲が狭いので、あまり詳しいとはいえません。しかし、技術屋の端くれとして設計段階での計算のステップをできる限り省かないようにと、Excelを使ってきました。近年はシミュレーションも手軽にできるようになったので、シミュレーションの段階で定数を取っ替え引っ替えする方法もありますが、やはり計算で定数を出した上でシミュレーションを行う、という手順が望ましいと思います。
そのような場合、面倒がらずに計算をするためにもExcelは良きツールであると思います。
それでは Best 73 & 88!
ジャンク堂 バックナンバー
- 第24回 オペアンプ入門(24)
- 第23回 LTspiceのススメ(後編)
- 第22回 LTspiceのススメ(前編)
- 第21回 (今日のジャンク)AZDEN DX-327というダイナミックマイクを復活させる
- 第20回 エクセルを使って空芯コイルのインダクタンスを計算する
- 第19回 電波防護指針に基づく電界強度を計算してみる
- 第18回 電子回路の放熱
- 第17回 秋月電子のレベルメーターキットを作る
- 第16回 FT8とALC、そしてスプラッタ
- 第15回 オシロスコープの50Ω終端器
- 第14回 差動アンプ 他 オペアンプ入門(14)
- 第13回 アクティブフィルタ オペアンプ入門(13)
- 第12回 RIAAとJIS A特性の等価雑音帯域幅とLTspice(オペアンプとノイズ おまけ編) オペアンプ入門(12)
- 第11回 オペアンプとノイズ(後半) オペアンプ入門(11)
- 第10回 オペアンプとノイズ(前半) オペアンプ入門(10)
- 第9回 オペアンプ入門(9)
- 第8回 オペアンプ入門(8)
- 第7回 オペアンプ入門(7)
- 第6回 オペアンプ入門(6)
- 第5回 オペアンプ入門(5)
- 第4回 オペアンプ入門(4)
- 第3回 オペアンプ入門(3)
- 第2回 オペアンプ入門(2)
- 第1回 ジャンク堂開店。オペアンプ入門(1)
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定