今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第12話 同一周波数のサイン波のかけ算と位相のはなし
2023年2月1日掲載
第11話までは、三角関数の掛け算の基本形である「周波数変換」と、周波数変換を実現する為に使用される「ミキサ回路」を取り上げました。これは周波数𝑓1と周波数𝑓2という異なる周波数のサイン波を掛け算する事で、𝑓1+𝑓2、𝑓1−𝑓2という異なる周波数の信号を得る回路でした。第12話からは「同一周波数のサイン波」同士の掛け算について取り上げます。
1. 同一周波数のサイン波の掛け算で得られるもの
まず、これまでのお復習いです。図1は第1話の図2の再掲です。振幅が等しく、𝑓1と𝑓2という異なる周波数のサイン波①と②を掛け算すると、三角関数の加法定理に従い、元の𝑓1,𝑓2の成分はなくなり、振幅が半分で周波数が𝑓1+𝑓2(和周波)、𝑓1−𝑓2(差周波)の成分の和に変換されました。
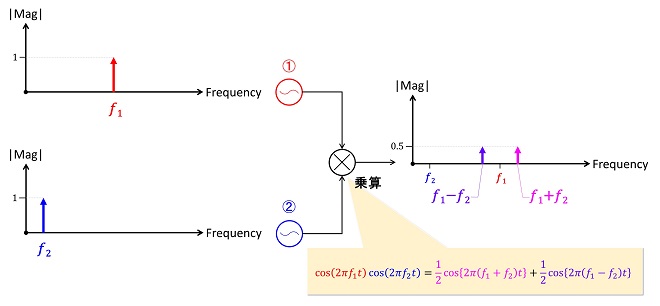
図1 周波数𝑓1と周波数𝑓2の掛け算(第1話の図2の再掲)
では、この考え方に従って、周波数𝑓1のサイン波①に同じ周波数の別のサイン波②を掛け算すると、どうなるでしょうか。同一周波数であっても三角関数の加法定理は成立するので、結果は図2のようになります。
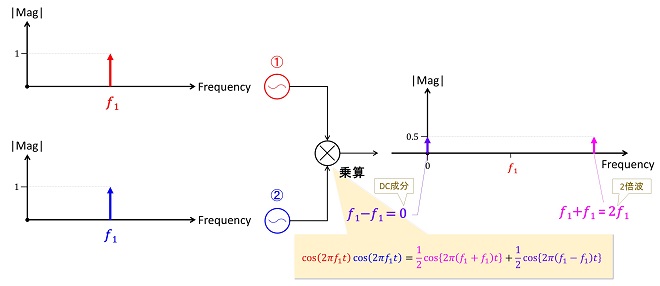
図2 同一周波数のサイン波どうしの掛け算(スペクトラム)
つまり、元の振幅の半分の大きさで、和周波成分は元の周波数の2倍、差周波成分は0Hzすなわち直流成分に変換されます。このときの時間応答波形を図3に示します。

図3 同一周波数のサイン波どうしの掛け算(時間応答波形・𝑓1=1MHz)
図3において、サイン波①とサイン波②は振幅=1(最大値)、周波数=𝑓1=1MHzでぴったり一致した波形です。これを時間軸上で掛け算すると、右上のグラフに示すように振幅=0.5(最大値)、周波数=2MHzのサイン波が現れますが、よく見ると+0.5だけ振幅がオフセットされています。このオフセット分が、図2に示した「DC成分」です。つまり掛け算して得られた波形をLPFに通す(あるいは平均化する)と元の振幅の半分の大きさの直流が出力され、HPFに通す(あるいはDCカット(微分)する)と、元の振幅の半分の大きさの2倍波が得られます。
2. 位相差
第1話から第11話までは話を簡単にする為に「位相」の概念を無視して解説してきました。オシロスコープを使ったことのある方なら直感的に理解頂けると思いますが、実際の交流波形は時間の関数なので、たとえ周波数と振幅が同じであっても「何時から振動し始めたか(または振動し始めた時の初期値)」によって同一時刻に観測される電圧は異なります。つまり同じ形の波形であっても時間軸上の位置は意図的に揃えない限りバラバラであり、図3のように波形がきれいに揃う事はありません。この「時間軸上の位置」の事を、我々は「位相」と呼んでいます。これまで交流電圧の瞬時値 𝑣 を表す式は、最大値を𝑉𝑚、角周波数をω(=2π𝑓、𝑓は周波数)とおいて
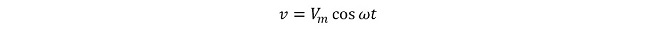
(式2-1)
と表記してきましたが、実際には位相 𝑝(初期位相と表記する教科書もあります)が加わり、
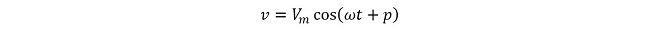
(式2-2)
と表記するのが本来の姿です。位相𝑝は角周波数ω[rad/sec]のオフセット(初期値)に相当する値なので、角度の単位(rad)で表現されます。また2つのサイン波の位相の差分を位相差と呼びます。では周波数が同じで位相差のあるサイン波を掛け算すると、どのような波形が生成されるのでしょうか。計算した結果を図4に示します。

図4 位相の異なる周波数𝑓1と周波数𝑓1の掛け算(時間応答波形)
図4は図3と同じ1MHzのサイン波どうしを掛け算した際の時間応答波形を示しますが、サイン波①を基準に、サイン波②の位相を±π[rad]の範囲でπ/4[rad]ステップで変化させたときの乗算結果を示しています。サイン波②のグラフと乗算した結果のグラフにおいて破線で示した波形が図3で示した位相差なしの波形に該当します。
乗算した結果のグラフ(右上)を見ると、サイン波①と②の位相差が和周波成分(2倍波)の位相差にそのまま反映(時間差に換算すると半分になっています)されており、さらに位相差に応じてDCオフセットの大きさが変化している事が判ります。DCオフセットの状態を詳しく見る為に、0.5μsecの移動平均処理(LPFと等価)を行ったのが右下のグラフで、サイン波①とサイン波②の位相差に応じて±0.5の範囲でオフセット値が変化している事が判ります。
3. なぜオフセット電圧が発生するのか?
ここまで見ると、なんだか同一周波数のサイン波を掛け算したときだけ、特別な事象が起きているように思えてしまいますがそうではありません。
二つのサイン波の掛け算においては、サイン波相互の位相差※1が掛け算した結果にそのまま反映されます。そして二つのサイン波が同一周波数になると差周波成分については0[Hz]なので、初期位相差の値のまま、時間tが経過しても振幅が変化しない状態になっているのです。計算式で見てみましょう。(式3-1)は第1話の(式2-10)の再掲です。
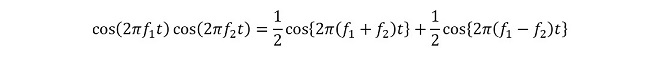
(式3-1)
この式を(式2-2)に倣って交流電圧𝑣1と𝑣2の積(電圧振幅𝑉𝑚と位相角𝑝を含む式)に書き換えてみましょう。まず交流電圧𝑣1と𝑣2は次式で表されます。
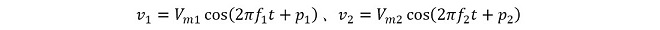
従って両者の積は三角関数の加法定理から
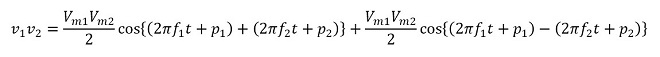
和周波成分、差周波成分それぞれのcos{ }の中を周波数(tの関数)の項と位相(定数)の項に分けて整理すると(式3-2)が得られます。
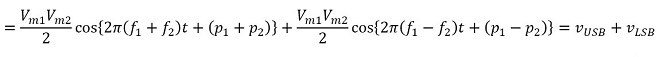
(式3-2)
まず和周波の成分𝑣USBを見てみます。(式3-2)から和周波成分のみ取り出したのが(式3-3)です。

(式3-3)
この式から、和周波成分𝑣USBの
(1) 最大振幅は𝑣1と𝑣2それぞれの最大振幅の積の1/2になります。
(2) 周波数は𝑣1と𝑣2それぞれの周波数の和になります。
(3) 位相は𝑣1と𝑣2それぞれの位相角の和になります。つまり片方の波形を基準(0deg)に見ると、元の位相進み/遅れの関係が掛け算結果に維持されます。
と言うことがわかります。
同様に(式3-2)から差周波成分𝑣LSBのみ取り出したのが(式3-4)です。
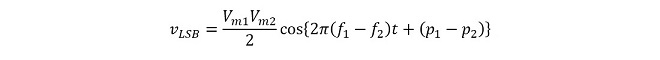
(式3-4)
この式から、差周波成分𝑣LSBの
(1) 最大振幅は𝑣1と𝑣2それぞれの最大振幅の積の1/2になります。(和周波成分𝑣USBと同じ)
(2) 周波数は𝑣1と𝑣2それぞれの周波数の差になります。
(3) 位相は𝑣1と𝑣2それぞれの位相角の差になります。つまり片方の波形を基準(0deg)に見ると、元の位相進み/遅れの関係が逆転するかたちで掛け算結果に維持されます。
要するに、同一周波数であろうとなかろうと、交流電圧𝑣1と𝑣2の積には両者の位相情報も反映されています※1。そして同一周波数の掛け算の場合は(式3-4)のt の関数となる項(2π(𝑓1-𝑓2 )t )がゼロになるため、(式3-4)は交流電圧𝑣1と𝑣2の位相差のみできまる定数となります(式3-5)。
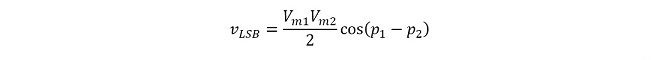
(式3-5)
(式3-5)を見れば自明ですが、同一周波数のサイン波を掛け算したときの差周波成分は図5に示すように2つのサイン波の位相差のコサインになります。
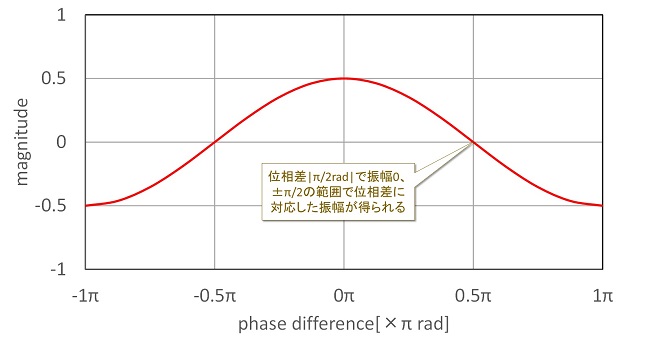
図5 周波数𝑓1×𝑓1の差周波成分𝑣LSBと掛け算したサイン波の位相差の関係
つまり、同一周波数のサイン波の掛け算は、掛け算する相手との位相差を検出する手段として利用することができます。
※1: 異なる周波数の交流電圧の間での「位相差」は時間と共に変化してゆきます。ここでいう「位相差」は、各波形のとある瞬間の位相の関係を示します。
4. 帯域を有する信号の場合
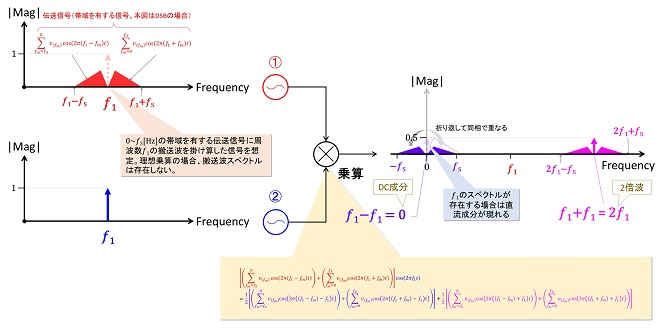
第3話で解説したように帯域を有する信号、例えば無線通信機の中間周波数(IF)回路等のように、伝送信号に搬送波信号が掛け算された信号を扱っている場合、この信号に搬送波と同じ周波数のサイン波を掛け算すると、図6に示すように、搬送波周波数の成分が直流に変換されるので、元の伝送信号を取り出すことができます。この処理を「復調」と言います。
この場合、搬送波のスペクトルが存在する場合は取り出された伝送信号に直流が重畳され、搬送波のスペクトルが存在しない場合は伝送信号のみが取り出されます。図6では乗算された結果、マイナスの周波数が発生する事が示されていますが、マイナスの周波数については後日解説したいと思いますので、ここでは0Hzで折り返して重畳されているとだけ理解しておいてください。
5. 第12話のまとめ
以下、第12話の要点を整理します。
- (1) サイン波(交流電圧)を定義するパラメータには「最大振幅𝑉𝑚」「周波数𝑓(または角周波数ω)」に加えて「位相(初期位相)𝑝」が存在する。
- (2) サイン波どうしを掛け算すると和周波成分の位相は両者の位相の和、差周波成分の位相は両者の位相の差になる。
- (3) この結果、同一周波数のサイン波(交流電圧)どうしを掛け算すると差周波成分は両者の位相差のコサインに相当する直流成分になる。
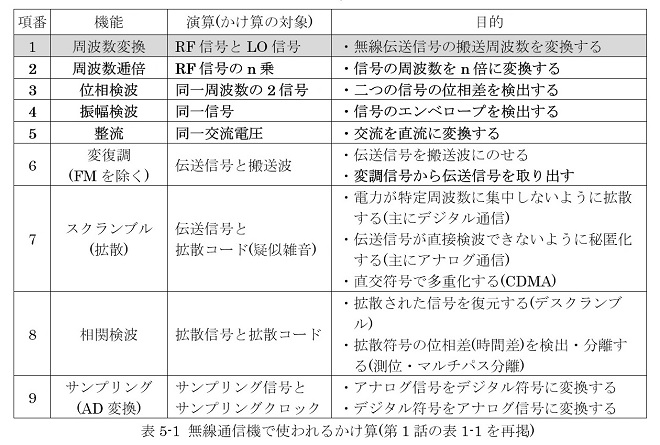
表5-1は第1話の表1-1の再掲です。同一周波数のサイン波の掛け算で実現する機能は、主に和周波成分を利用する「2.周波数逓倍(2逓倍)」と差周波成分から得られる位相情報または直流成分を利用する「3.位相検波」「4.振幅検波」そして「5.整流」の4機能です(何れも太字で示した項)。このうち2と5は同じ信号同士の掛け算(つまり自信号の2乗)で実現される機能、3は同じ周波数の別々の信号の掛け算で実現される機能、4はその両方のパターンが存在します。次回からは項番3の「位相検波」を取り上げる事とし、その代表用途であるPLLの基本について解説します。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)