今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第16話
ループフィルタとPLLの応答特性の話(その1)
2023年6月1日掲載
第15話では位相検波器に要求される特性とデジタルの位相検波方式について解説しました。第16話からはループフィルタの役割について解説します。PLLに使用される位相検波器は、アナログ乗算方式にせよ、デジタル方式にせよ、位相差を示す直流電圧を直接出力しません。アナログ乗算器の場合は2倍波成分の除去(第12話)、デジタル方式の場合は検波出力の時間積分を行う(第15話)事で、位相差を示す直流電圧を得る事ができます。従ってローパスフィルタ(LPF)は必要不可欠となるのですが、LPFと呼ばずにループフィルタという名称がつくのは何故でしょうか。今回はこのあたりを解説したいと思います。
1. とりあえず用語の説明
PLLのようなフィードバックを有する系の解析は「自動制御」の分野で「フィードバックシステム」として手法が確立されており、電子回路の分野でも同じ概念が導入されています。図1は自動制御でいう「フィードバックシステム」をモデル化したものです。周波数特性の解析にフーリエ変換ではなくラプラス変換を使用したり、利得(Gain)を伝達関数と称したり、回路屋とは微妙な言葉の違いがあります。と言うことで、まずはフィードバックシステムの解析に登場する用語とその定義について説明します。
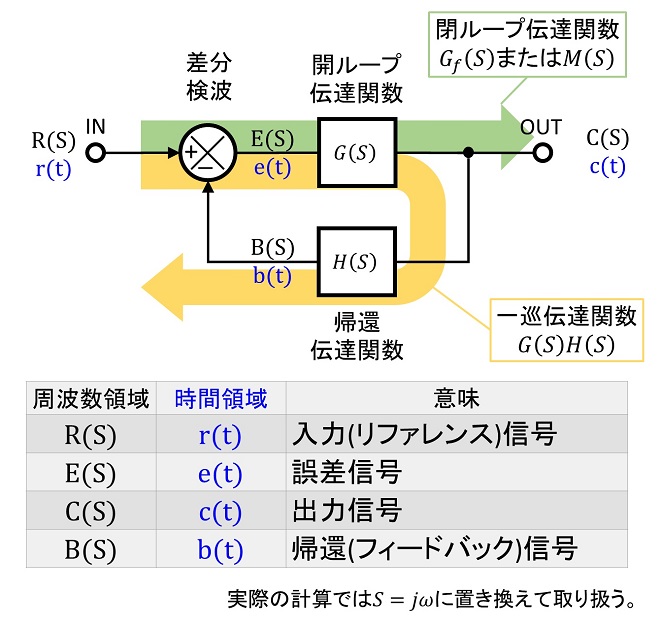
図1 一般的なフィードバックシステムの信号呼称と伝達関数の名称
(1) 時間領域と周波数領域の表現
アナログ回路解析では連続信号を扱う事が多いので、信号をサイン波の集合体(過去から未来までずっと続いている信号)で定義し、そのフーリエ変換で周波数応答を導出するのが一般的です。これに対して自動制御の世界では「時刻t1からt2秒後の状態」というように「始点」が存在する信号を多く扱うため、フーリエ変換では計算できない関数を扱うケースが発生することから、ラプラス変換が使われます。図1の表の周波数領域の列に書かれた関数は全てωではなくSという変数の関数になっています。実際の計算では“S”を“jω”に置き換えて扱います。ラプラス変換とフーリエ変換は数学的には別物なので、厳密にはこのように“S“としておく必要がありますが、回路計算に適用する範囲では“S”を“jω”と置き換えれば同じになると考えて実用上問題ありません。
(2) 伝達関数
回路の入出力の関係を示す関数の事で、いわゆる「利得(Gain)」に該当するパラメータです。入出力インピーダンス(反射特性)の概念はありませんが、「Mr. Smithとインピーダンスマッチングの話【第10話】Sパラメータの基礎」で解説した4端子パラメータとよく似た概念になります。ネガティブフィードバックシステムの特性を表現する伝達関数は全部で4種類あり、いずれも周波数領域の特性で定義されます。
- ①開ループ伝達関数 G(S)=C(S)⁄E(S) :
フィードバックがかからない状態での入力→出力方向の伝達関数。SパラメータでいうS21に該当します。 - ②帰還伝達関数 H(S)=B(S)⁄C(S) :
フィードバック回路の伝達関数。SパラメータでいうS12と似たパラメータです。 - ③一巡伝達関数 G(S)H(S)=B(S)⁄E(S) :
入力信号がG(S)倍されて出力端子に至り帰還伝達関数H(S)倍されて入力(差分検波の部分)に戻るまでの伝達関数です。G(S)H(S)で導出されます。Sパラメータでは、S21×S22×S12がこれに該当します。 - ④閉ループ伝達関数 G𝑓(S)またはM(S)=C(S)⁄R(S) :
ネガティブフィードバックループを閉じた状態の入力→出力方向の伝達関数です。①~③から(式1-1)で導出されます。
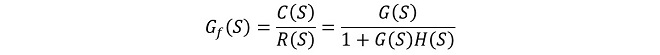
(式1-1)
4端子回路網理論において、4つのパラメータと入出力の整合状態から実質的な順方向利得が算出されるのと同じイメージです。
2. フィードバックすると何が問題になるのか?
通常、「電子回路は電子が移動する早さで応答するので入出力間の応答遅延時間は限りなく小さい」と考えますが、電子回路の応答時間は有限であり、入力信号が変化してからその変化が回路の出力に反映されるまでには、必ず有限の時間が必要です。フィードバックシステム内に信号遅延が存在する場合、フィードバック信号の遅れが誤差要因となります。これを位相誤差(Phase Error)で示したのが図2です。
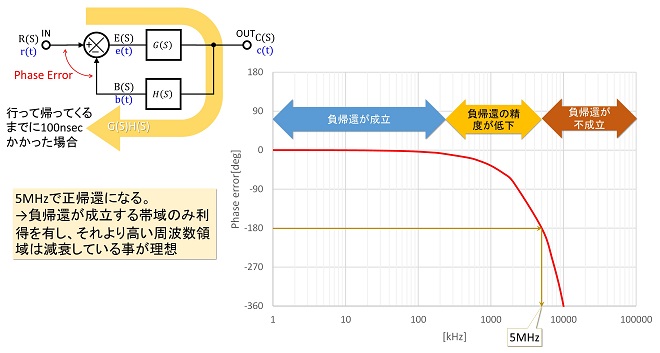
図2 入力信号の変化が帰還信号の変化に反映されるまでに100nsec要した場合の信号位相差
図2では入力信号の変化から帰還信号の変化までの遅延時間tdが100nsec(0.1μsec)あった場合の一巡伝達関数H(S)の位相項のみを計算したものです。これは(式2-1)で導出することが可能です。
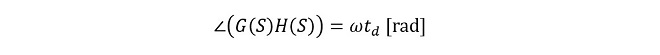
(式2-1)
遅延が存在するので、入力信号と帰還信号の位相差は、入力周波数が上昇するのに伴い大きくなります。この結果、図2では入力信号の周波数が5MHzに達したところで位相差が-180deg、つまり逆相になることを示しています。「逆相になる」とは、負帰還回路として動作していたフィードバックループが、この周波数では正帰還回路として動作してしまうと言うことです。このような周波数特性をもつフィードバックループの場合、閉ループ伝達関数G𝑓(S)はどのようになるのでしょうか。仮にこのtdがG(S)にのみ発生しているものと想定して、図2のフィードバック系に下記の通り利得を定義した場合の閉ループ伝達関数を計算してみます。
開ループ伝達関数の絶対値 :|G(S)|=10
帰還伝達関数の絶対値 :|H(S)|=0.15
とすると
開ループ伝達関数 :G(S)=10 cos ωtd + j 10 sin ωtd
帰還伝達関数 :H(S)=0.15 + j 0
この時、ネガティブフィードバックループの閉ループ伝達関数は(式1-1)から
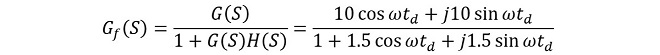
(式2-2)
この式にtd=100[nsec]、と角周波数を代入してExcelで計算しグラフにしたのが図3です。
図3では話を判りやすくする為に増幅器(オペアンプ)のイメージで表現しています。2つあるグラフは閉ループ伝達関数G𝑓(S)を示しており、このうち上側(青のグラフ)が振幅特性(入出力利得)、下側(オレンジの実線グラフ)が位相特性(入出力位相)です。下側のオレンジの破線は図2に示した一巡伝達関数H(S)の位相特性を転記したものです。
本図においてPhase Errorが充分小さい(オレンジ破線のグラフがほぼ0の)周波数領域、すなわち ωtd ≅ 0 の領域では、(式2-2)は
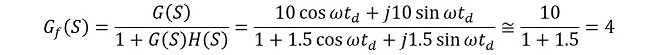
(式2-3)
となって系全体は振幅利得12dB(4倍)のフィードバックアンプとして動作しています。しかしPhase Errorが大きくなってくると閉ループ伝達関数G𝑓(S)の振幅特性(青のグラフ)は上昇し始め、Phase Errorが180degとなる周波数(5MHz)でピークが生じています。この周波数ではフィードバックにより利得がどんどん上昇するため、R(S)もしくはB(S)に5MHzの信号成分が一瞬でも存在すれば、それをきっかけに所謂「ループ発振」の状態に陥ります。
閉ループ伝達関数H(S)の位相特性(オレンジの実線グラフ)は一巡伝達位関数H(S)の位相特性と比較して、最初は位相回転が緩やかですが、途中で位相変化が減少から増加に転じ、Phase Errorが180degとなる周波数(5MHz)では0degに戻っています。その後Phase Errorは+(位相進み)に転じ、2倍の周波数(10MHz)で再度0degに戻ってきます。
ちなみに、このグラフの形状は回路屋さんには「共振特性」としてなじみのある応答ではないかと思います。図3の5MHz前後の特性は実際にフィードバックループが共振している状態です。共振回路と電子デバイスの共振については「Mr. Smithとインピーダンスマッチングの話【第8話】直列共振と並列共振」、「Mr. Smithとインピーダンスマッチングの話【第9話】直列共振と並列共振2」で解説しました。電子デバイスの共振では伝達関数ではなく反射特性の位相回転で共振を語ることになりますが、デバイスの端子間や配線の電気長が波長に対して無視できなくなるとインピーダンス特性にピークが生じる現象と、フィードバック信号B(S)の遅延が信号周期に対して無視できなくなると発生する図3の現象は類似の考え方です。なおこの応答は周期的に繰り返されるのですが、図3のグラフでは計算粒度の関係でうまく見えていません。
3. ループフィルタの役割
以上解説した通り、出力から入力に信号をフィードバックする回路は、回路遅延がゼロでない限り、フィードバック信号B(S)の位相が逆転して設計通りに動作できなくなる周波数が必ず存在します。このポイントを「極」といいます。この宿命ともいえる特性に対処するため、フィードバック系を有する回路(システム)においては、フィードバック信号B(S)の位相ずれが無視できなくなる周波数より高周波域では、一巡伝達関数H(S)の絶対値(すなわち利得)が1以下(0dB以下)になっている必要があります。この条件を満足させる為に必要となるのが“ループフィルタ”と呼ばれるLPF(ローパスフィルタ)なのです。ここでは図3のフィードバック系に図4に示すループフィルタを組み込んでループ発振を回避できるか検討することにします。
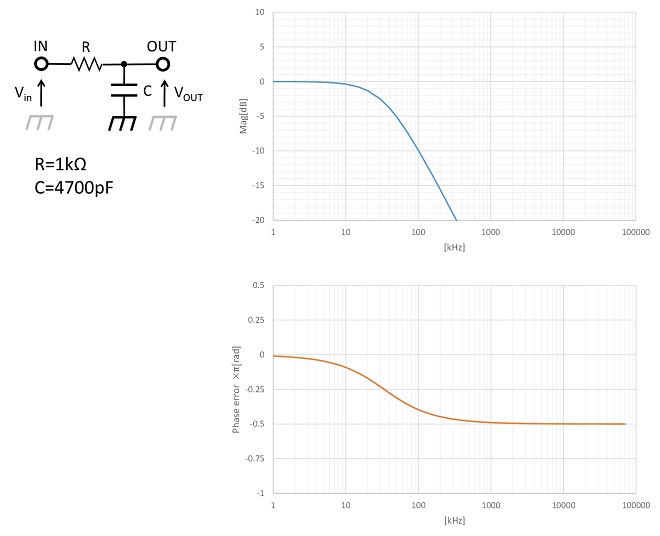
図4 図3のフィードバック系に組み込むループフィルタ
このフィルタは単純なRCフィルタです。カットオフ周波数(利得-3dBポイント)が約34kHzで、そこから-6dB/octの減衰特性を有します。通過位相は-π/2[rad](-90deg)に漸近する特性になります。伝達関数F(S)を(式3-1)に示します。
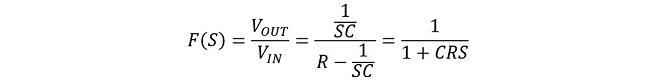
但しS = jω (式3-1)
これは一般的なRCフィルタの入出力特性を示す計算式です。このフィルタを図3のフィードバック系に組み込んで閉ループ伝達関数がどのように変化するかを計算したのが図5です。
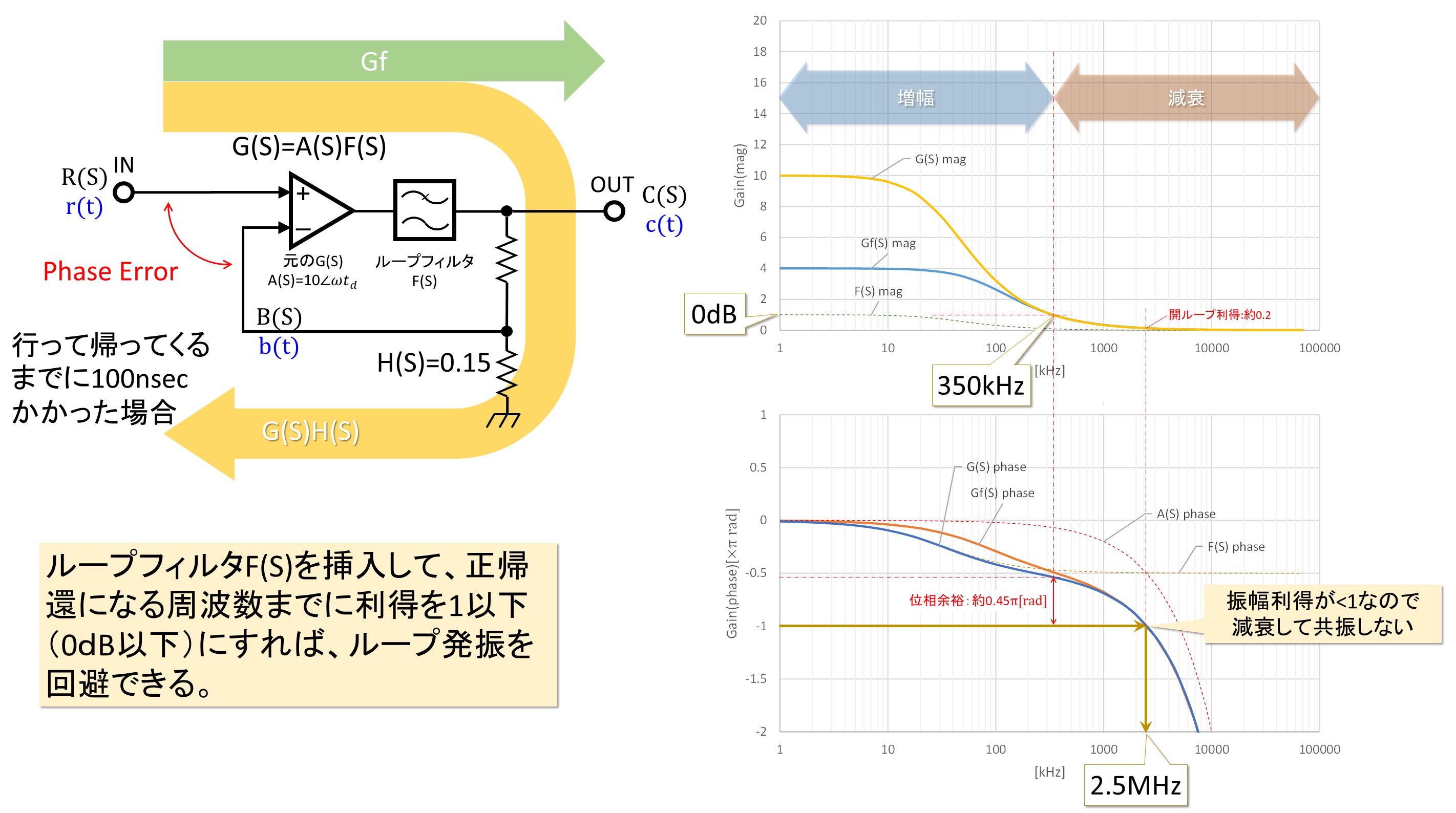
新しい伝達関数F(S)が増えたので、図3においてG(S)と一括りにしていたフォワード系の伝達関数をA(S)という記号に改めました(図3から引き続きアンプのイメージで記述しています)。図5における開ループ伝達関数G(S)は、図3から改めて、G(S) = A(S)F(S)となります。
ループフィルタF(S)が挿入された結果、図3では|G(S)|の値はずっと10倍でしたが、図5では|F(S)|の特性が反映されて約350kHzで1倍(0dB)となります。それ以上の周波数に於いて|G(S)|は-20dB/decで“0”に近づいて行きます(つまり350kHz以上の周波数の信号は減衰していきます)。次に一巡伝達関数H(S)の位相(図でPhase Errorと記載したポイントでの位相差に相当。G(S) phaseのグラフと完全に重なるため図5では省略しています。)は、図3では100kHz付近から徐々にマイナス方向に振れ始め、5MHzで-π[rad]に達しました。図5では新たにH(S)が挿入されたため、10kHz付近から位相回転し始めますが、F(S)による位相回転が0.5π[rad]を超えない※ので、マイナス方向への位相の振れは-0.5π[rad]で一旦落ち着き、以降はA(S) phaseのグラフに沿って位相が回転します。この結果、Phase Errorが-π(-180deg)となる周波数は5MHz→2.5MHzと低くなっていますが、上記の通り、350kHz以上の周波数帯では|G(S)|の値が1以下(0dB以下)となっているため、出力信号が正帰還されてもループの中で減衰するため、図3で見られたような共振(発振)が起きることはありません。極の周波数でも安定であることを定量的に表現する方法として、「位相余裕」、「利得余裕」というパラメータが良く用いられます。位相余裕とは、一巡伝達関数H(S)の振幅利得が0dBとなる周波数に於いて、一巡伝達関数H(S)の位相が-π[rad](-180deg)からどれだけ離れているかを示すパラメータ。利得余裕とは、一巡伝達関数H(S)の位相特性が-π(-180deg)となる周波数に於いて、一巡伝達関数H(S)の利得が1よりどれだけ小さいか(マイナス何dBか)を示すものです。図5の場合、位相余裕は350kHzの点で約0.45π[rad](81deg)、利得余裕は2.5MHz付近で約0.2(-14dB)となります。
※回路を構成するデバイスの自己共振周波数よりも充分低い、つまりフィルタ入出力間の伝搬遅延が入出力周波数の周期に対して充分小さい周波数領域を想定した解説です。
4. 第16話のまとめ
第16話では、フィードバック系における伝達関数の表記と考え方、ならびに何故ループフィルタが必要になるのかについて解説しました。出力の一部を入力に戻して誤差を補正するネガティブフィードバックシステムにとって、処理系統の遅延の影響は避けて通れない問題です。オペアンプのように、帰還信号の位相回転が問題になるまえに利得が減少するように設計されているデバイスを除き、一般的なフィードバックシステムにおいては、フィルタによる帯域制限は必須となります。以下、第16話の要点をまとめます。
- ①フィードバック制御系の周波数領域での特性記述はS(=jω)を用いて表記し、時間領域の応答解析はラプラス逆変換を使用する。
- ②フィードバック制御系の入力信号とフィードバック信号の間には、信号がループを一巡分する為に必要な遅延時間があり、この遅延時間による位相誤差が必ず発生する。
- ③この位相誤差がπ[rad](180deg)に達するポイントを極と呼ぶ。極は負帰還だったループが正帰還に転じるポイントであり、閉ループの伝達関数G𝑓(S)が共振特性と同等の振る舞いをする。
- ④極の周波数で一巡伝達関数H(S)に振幅利得があるとループ発振が生じる。
- ⑤ループの安定度を定量的に示すパラメータとして
位相余裕: 一巡伝達関数H(S)の振幅利得が0dBとなる周波数に於いて、一巡伝達関数H(S)の位相が-π[rad](-180deg)からどれだけ離れているか、
利得余裕: 一巡伝達関数H(S)の位相特性が-π(-180deg)となる周波数に於いて、一巡伝達関数H(S)の利得が1よりどれだけ小さいか(マイナス何dBか)
の2つが利用される。
「フィードバック系」という一般化した表現なので、取り付きにくいという方もおられたかもしれません。今回ご説明した言葉や概念は、PLLのみならず、オペアンプのフィードバック回路、無線機のAGC、APC、ALC、AFC等の制御機能、さらにはサーボモータなどの電機系フィードバック制御などに対する共通の理論体系なので、考え方が理解できると他の分野でも役に立つと思います。次回はPLLの伝達関数について解説します。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)