今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第17話
ループフィルタとPLLの応答特性の話(その2)
2023年7月3日掲載
第16話では、フィードバック系における伝達関数の表記と考え方、ならびに何故ループフィルタが必要になるのかについて解説しました。フィードバック系と呼ばれるシステムの概念はご理解頂けたでしょうか。引き続き第17話ではPLLの伝達関数について解説します。
1. PLLの要素機能と伝達関数
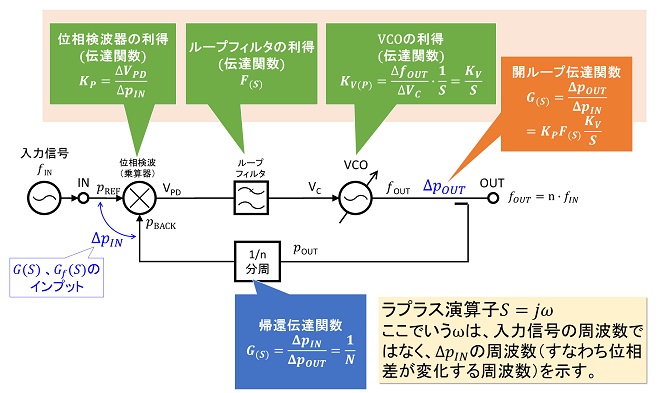
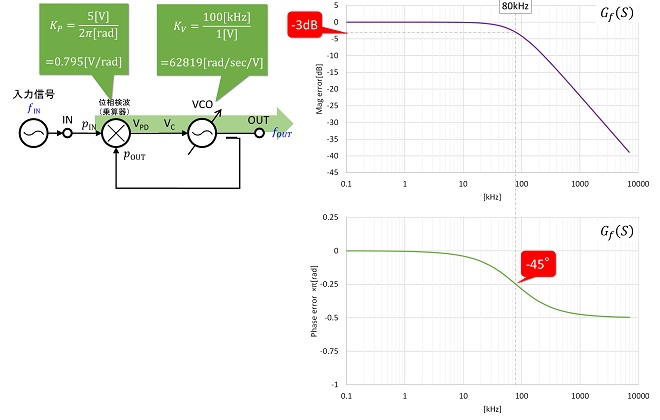
フィードバックシステムとして捉えたPLLの機能系統図と伝達関数を図1に示します。第16話の図1に示したフィードバックシステムの開ループ伝達関数G(S)の部分を構成するのが、位相検波器、ループフィルタ、VCOで、帰還伝達関数H(S)を構成するのがフィードバックカウンタ(1/n分周器)となります。PLLシンセサイザにおいてはこれ以外にリファレンス信号を分周する1/mカウンタ(第14話の図4参照)が存在しますが、フィードバックループの外側なので、伝達関数には含まれません。では各構成要素の伝達関数を見ていきましょう。
(1) 位相検波器の伝達関数
位相検波器はpREF , pBACKの2つの入力端子と一つの出力端子VPDを持ち、2つの入力端子間の位相差pINに比例する電圧VPDを出力します。理想の位相検波器においては、入力位相差の変化∆pINと出力電圧の変化∆VPDの間に周波数依存性はなく、その伝達関数KPは(式1-1)で表されます。
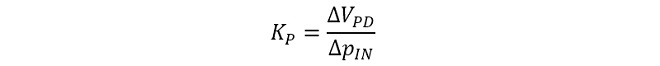
(式1-1)
(2) ループフィルタの伝達関数
ループフィルタの伝達関数F(S)は、フィルタの回路構成により複数のパターンに分かれる為、後述します。ループの動作安定と追従精度を確保するために、F(S)を除く伝達関数の特性に合わせて回路構成を選定する事になります。
(3) VCOの伝達関数
VCOはオシレータで、1つの入力端子VCと出力端子fOUTを有し、発振周波数fOUTがVCに比例します。従ってVCOの伝達関数KVは、
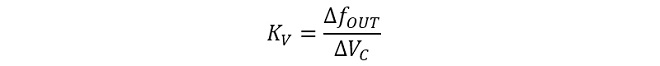
(式1-2)
となります。KVはVCOの変調感度と呼ばれることもあります。(式1-2)は制御電圧VCと出力周波数の関係を示しており、VCと出力位相の関係ではないため、このままではPLLの設計に適用する事ができません。結論から言うとVCを変化させたときの出力端子の位相変化を表す伝達関数KV(P)は、KVを時間で積分した値(式1-3)となり、周波数領域ではこれをラプラス変換して(式1-4)の通りになります。
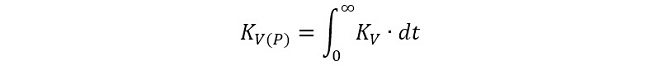
(式1-3)
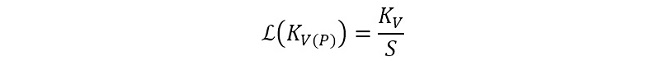
(式1-4)
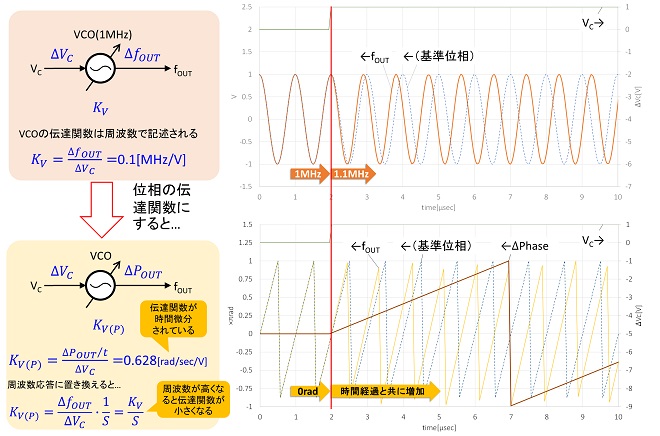
世間の教科書ではこの程度の解説で済ませているケースが多いのですが、ここではその物理的な意味を考察することにします。VCが変化したとき、出力位相はどのように変化するのかを模式的に示したのが図2です。この図は、あるVCでの発振周波数が1MHz、そこからVCを変化させた時の変調感度KV=100kHz/VのVCOを仮定してExcelで作図したものです。図2の上のグラフはVCを1Vステップ変化させたときの出力瞬時電圧の変化(すなわちサイン波)を示しています。周波数の変化がわかりやすいように、破線で1MHzのサイン波を重ねています。下のグラフは各サイン波の位相角の時間変化と、破線のサイン波を基準としたときの位相差を示しています。
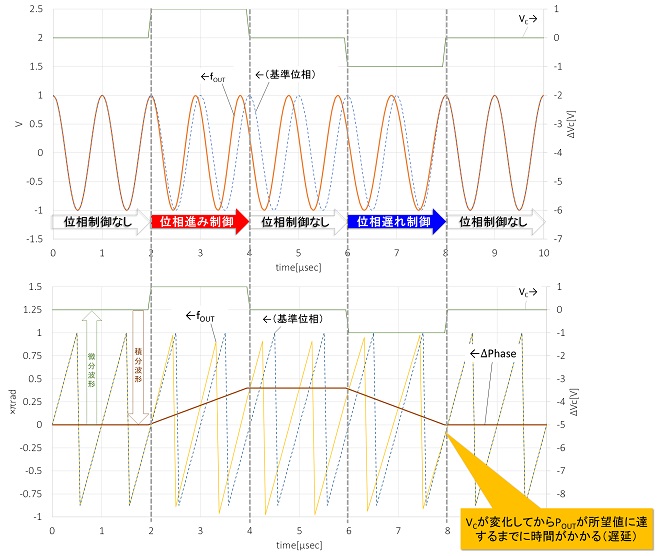
周波数(角周波数)とは単位時間内に位相が何回転するか[cycles/sec](→[Hz])を表す諸元ですが、言い換えると位相が回転する速さ[rad/sec](→角速度)を示す諸元です。従って物理的には位相の時間微分値ということになります※。従って、周波数を上昇させると位相の回転速度は早くなりますが、実際に位相が元の信号より進むには時間を要することになります。故に周波数の伝達関数を位相の伝達関数に変換するためには時間での積分が必要となり、周波数領域においては1/S = 1/jωが乗算されて制御周波数が高くなるほど伝達関数が小さくなるという特性になります。図3は実際にVCOで位相進み→位相遅れ制御を行ったイメージを示したものです。
※位相と位相差という言葉に注意!
交流において位相差はじっとしているが位相はじっとしない諸元。
VCの値を階段状に1V上昇させると、発振周波数は1MHzから1.1MHzに上昇しますが、位相は周波数の上昇に伴って連続的に進んで行くので、すぐには変化しません。VCを1V上昇させた状態を一定時間継続させる事で、所定の位相差に達します。VCを下げたときも同様に位相は周波数の低下に伴って連続的に遅れて行くので、VCを1V下降させた状態を一定時間継続させることで、所定の位相差に達します。位相差(ΔPhase)のグラフとVCのグラフを見比べると、VCのグラフがΔPhaseのグラフの時間微分になっていることがお解り頂けるのではないかと思います。
(4) 1/n分周器の伝達関数
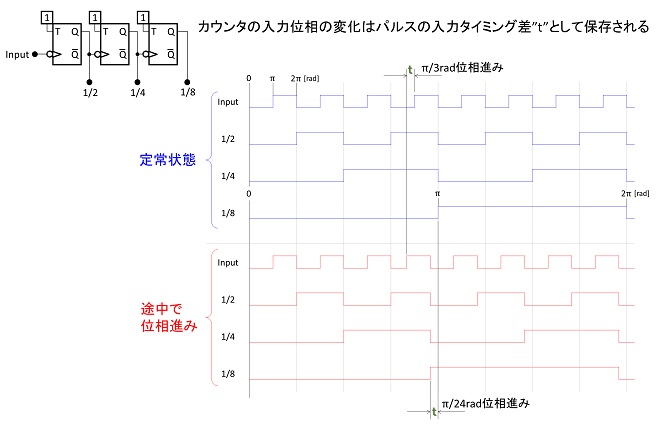
1/n分周器は入力信号 pOUTの周波数を1/nに分周して、pBACKとして出力する回路で、通常はデジタルカウンタが使用されます。図4はn=8としたときの分周器の入出力タイミングを示したものです。
フィードバック信号をデジタルカウンタで分周する際、入力信号(VCO出力)の位相変化はカウンタの入力端子に加わるクロック信号(パルス)のタイミング差として絶対時間tで出力信号に反映されます。一方で信号の周波数は分周されるため、分周数をNとすると出力信号の周期はN倍になります。この結果、出力信号の位相変化は入力信号の位相変化の1/Nとなります。従って1/n分周器の伝達関数は単純に1/N(単位なし)となり、周波数特性も持たない為、PLLの教科書では固有の名称を与えずに、1/Nと表記されています。
ちなみにN分周すると、入力信号の位相変化が1/Nになるということは、PLLシンセサイザのVCO出力においては、位相検波器の入力端子で維持している位相誤差のN倍の位相回転が発生しているという事になります。無線通信機用のシンセサイザの場合、Nの値は1000以上になることが普通なので、「位相同期」と言いながら、PLLの基準信号とVCO出力信号の瞬時位相は、事実上位相同期できてないと考えるべきでしょう。(周波数精度を議論する時間平均で見れば同期できています)
2. PLLの伝達関数
最後に図1に戻って、PLL全体の伝達関数について解説します。第16話で解説した通り、フィードバックシステムの伝達関数には、開ループ伝達関数G(S)、帰還伝達関数H(S)と、一巡伝達関数G(S)H(S)、閉ループ伝達関数G𝑓(S)が定義されます。
(1) 開ループの伝達関数
ループを開いた状態で定義される、開ループ伝達関数G(S)、帰還伝達関数H(S)は、それぞれの経路を構成する各ブロックの伝達関数の積となります。開ループ伝達関数G(S)は、(式1-1)、(式1-4)から
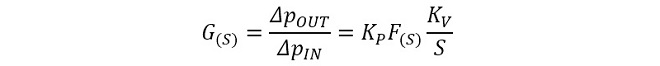
(式2-1)
帰還伝達関数H(S)は帰還経路が1/n分周器のみなので
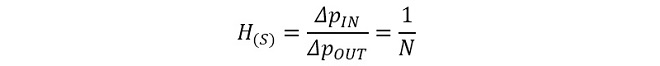
(式2-2)
一巡伝達関数は
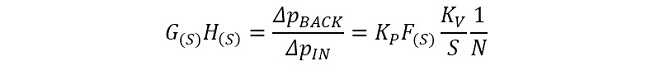
(式2-3)
となります。一巡伝達関数(式2-3)を見ると分母にSが存在します。これは入力電圧対周波数の関係で表現されたVCOの伝達関数KVを位相の伝達関数KV(P)に置き換えた際に現れたものでした(式1-4)。Sにはjωが代入されるので、この伝達関数は図5に示すように振幅が1/𝑓に比例する関数になり、位相は周波数に関係なく90°(π/2rad)遅れる特性を示します。
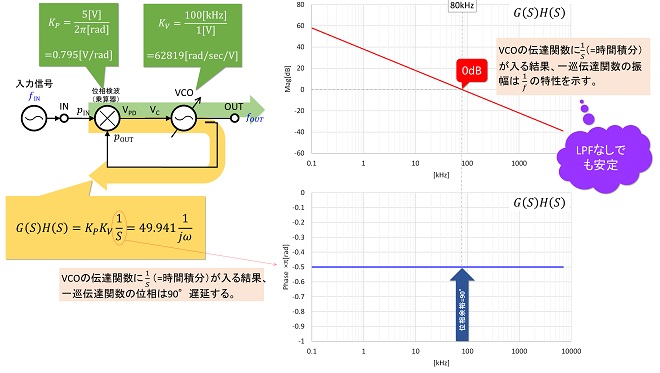
図5 ループフィルタなしで構成したPLL(仮想)の開ループ伝達関数
説明が前後してしまいましたが、図5は位相検波器の出力電圧範囲が0~5V(−π ~ +π)、VCOの変調感度を100kHz/Vと仮定して伝達関数を具体的に計算したものです。これまでにも述べましたが、図5においてグラフの横軸の周波数は入力信号𝑓INの周波数ではなく、入力信号𝑓INの“位相変動周波数”(位相変調周波数と考えても良い)を示しています。
もし位相検波器がリファレンス信号pREFとフィードバック信号pBACKの位相差に比例した直流電圧のみを出力する事ができれば、PLLは、この振幅が周波数に反比例する伝達特性のおかげでループフィルタがなくても、フィードバック信号の遅延の影響を受けずに安定する特性を示します。しかし残念ながら実際の位相検波器は、アナログ方式においては第12話で解説した通り2倍周波数成分を除去する必要がありますし、ディジタル方式においてはパルス信号を積分しないと位相差電圧が取り出せません。従ってループフィルタは必須であり、このPLLは机上でのみ作り出すことができる仮想のPLLといえます。
(2) 閉ループ伝達関数
この仮想PLLの閉ループ伝達関数を図6に示します。閉ループ伝達関数G𝑓(S)は、
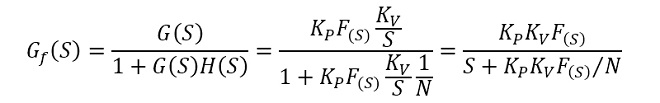
(式2-4)
となります。この仮想PLLは(式2-4)の分母がSの一次の多項式なので、一次ループと呼ばれる応答特性を示します。一次ループはステップ応答特性にオーバーシュート、アンダーシュートが生じないのが特徴ですが、ループ利得が充分に大きくないと、制御残差(誤差)が発生します。
図5において一巡伝達関数の振幅利得が0dBとなる周波数(約80kHz)において図6の閉ループ伝達関数の振幅が-3dB(電力半値)となり、位相は45°回転しています。この一巡伝達関数の振幅利得が0dBとなる点が、このループの極になります。極の周波数は図6に示した閉ループ伝達関数の通過帯域幅(電力半値幅)を示しており、一巡伝達関数の振幅利得が大きくなるほど高い周波数になることは、図5から容易に考察できると思います。
ループフィルタを使用しないPLLは「仮想PLL」としましたが、入力信号周波数の2倍波がループの応答帯域と比較して無視できる程高い周波数になる場合は、アナログ位相検波器を用い、LPFのカットオフ周波数をループの応答帯域外に設定することで、このようなPLLを構成する事も可能です。しかし、このPLLは制御誤差と閉ループの通過帯域幅の両方がループ利得のみで決定されるため、実用例を見たことはありません。
3. 第17話のまとめ
第17話では、PLLを構成する位相検波器、VCO等、個々の構成要素の伝達関数について解説し、最後にループフィルタなしで位相検波器とVCOを直結した仮想PLLの閉ループ伝達関数がどのようになるのかを示しました。このPLLは実用性に欠けるものの、PLLの基本特性を理解する上では良い教材だと思います。常々、PLLの制御理論をややこしくするのは、
①位相同期するシステムなのに、位相誤差情報で周波数を制御している事
②フィードバックループの周波数応答の「周波数」と入出力の「周波数」を混同してしまう事
につきると思います。今回は①について詳しく、②については要所要所で言葉を選びながら解説したつもりです。少しでも理解を深めて頂ければ幸いです。以下、第17話の要点をまとめます。
①位相検波器の出力電圧(位相差情報)でVCOを制御(周波数制御)したときの出力位相応答は、VCOの応答を時間積分した結果で示される。
②①は制御→応答までに時間遅れがあることを示しており、VCOの伝達関数の周波数特性には1/Sが乗算される。この事は、制御入力の感度特性が1/𝑓(ここでいう𝑓は制御信号の周波数)に比例し、かつ制御入力→出力変化の周波数特性に−90°の位相差があることを示している。
③フィードバック回路に挿入される分周器は分周数をnとすると伝達関数は1/nになる。これは位相検波器入力端子で∆pdet[deg]の位相誤差があった場合、VCO出力の位相誤差∆pVCOは、そのn 倍になっていることを意味する。
④閉ループ伝達関数の通過帯域幅は、一巡伝達関数の絶対値(振幅利得)が大きくなると拡大し、小さくなると縮小する。
実は、無線通信機で多用されるチャージポンプ式の位相検波器の場合は伝達関数が(式1-1)で示したような単純な計算式にはなりません。次回はこのあたりを中心に二次ループの振る舞いとループフィルタの使い方について解説します。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)