今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第18話
ループフィルタとPLLの応答特性の話(その3)
2023年8月1日掲載
第17話では、PLLを構成する位相検波器、VCO等、個々の構成要素の伝達関数について解説し、最後にループフィルタなしで位相検波器とVCOを直結した仮想PLLについて触れました。すべてのPLLはVCOの位相応答に時間積分の要素が含まれるため、伝達関数(利得)が周波数(ループ内の状態変化の周波数) 𝑓の逆数に比例します。この結果何もしなくてもループの帯域は制限がかかり、ループは安定すると解説しました。ところが世間で広く使用されているPLLはこのような安定特性を得ることができません。第18話はこのあたりのお話になります。
1. チャージポンプを用いたPLLの伝達関数
チャージポンプは第15話の図4で解説しました。2個のRSフリップフロップを組み合わせた回路構成で、PREF端子とPFB端子のどちらに先に信号エッジが入力されたかを保持して、出力端子に接続されたキャパシタを充放電することにより位相差を電圧に変換する回路でした。位相差のみならず周波数差についても大小関係が判別できることからPFDと呼ばれています。
(1) 位相検波器の伝達関数
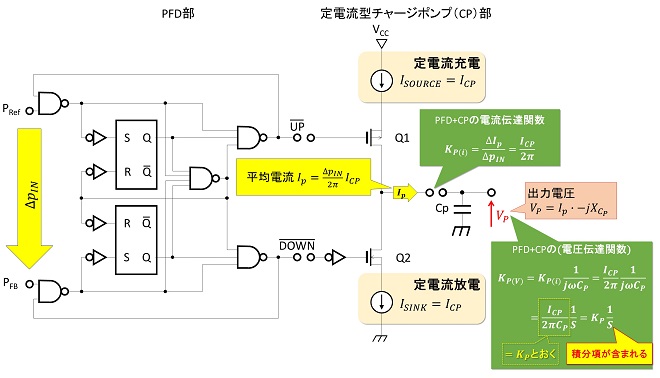
第15話の図4に示したチャージポンプは定電圧電源をスイッチして負荷のキャパシタを充放電する回路方式でした。昨今のPLL ICで主流になっているチャージポンプは、図1に示すように、定電流源をスイッチして負荷のキャパシタを充放電します。
定電流源を用いて充放電を行うので、チャージポンプ出力端子の平均電流IPが位相差に比例することになり、入力位相差と電流との関係を示す伝達関数KP(I)は定電流源の定電流値をICPとおくと、(式1-1)で与えられます。
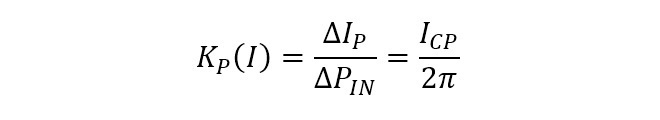
(式1-1)
キャパシタの端子電圧𝑉とチャージ電荷Qの関係はQ=CV、電流𝐼は単位時間あたりに移動する電荷の量を示す値ですから、チャージポンプの出力に接続されたコンデンサCPの端子電圧VPは(式1-2)に示すとおりとなります。
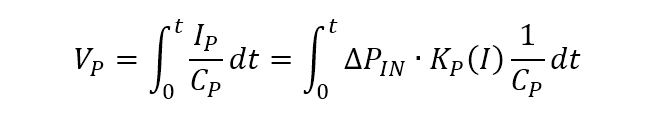
(式1-2)
周波数領域に変換すると
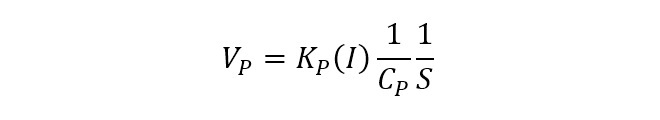
(式1-3)
つまりチャージポンプの出力に接続されたキャパシタの端子電圧VPはKP(I)をキャパシタの容量CPで割った値と時間の積・・・ すなわち時間で積分した値で表される事になります※1。この結果、定電流出力型チャージポンプの位相検波器を用いたPLLは図2に示すように位相検波器とVCOの2カ所に積分項持つ「二次ループ」のPLLとなります。
※1: 平均値ではなく積分値であることがポイントです。定電圧出力タイプのチャージポンプの場合は位相差一定の状態が継続したとき、出力電圧は一定値を保ちますが、定電流出力型チャージポンプの場合、位相差一定の状態が継続すると電圧値は時間経過と共に上昇します。
(2) 不安定な二次ループ
時間積分項を有する伝達関数をラプラス変換すると1/Sの項が現れるというのは、第17話で解説したとおりです。ラプラス変換の結果を周波数領域として扱うときはS=jωですから、1/Sの項が一つ現れると伝達関数の位相は90°遅れるということも第17話の図5で解説しました。
二次のループの場合、この1/S項が2つ存在するので、定電流型チャージポンプとVCOをループフィルタなしで直結すると、図3に示すように一巡伝達関数G(S)H(S)の位相は周波数に関係なく180°遅延する事になります。
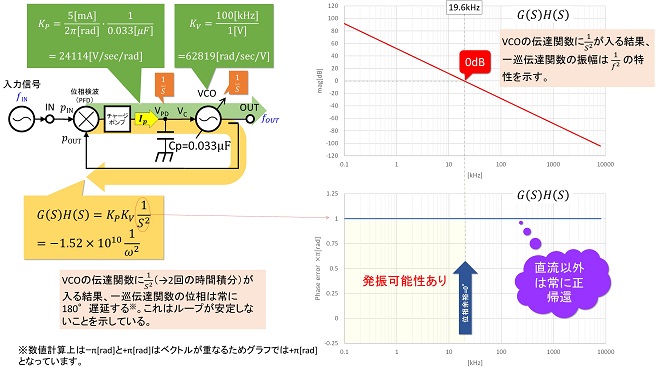
図3 定電流型チャージポンプとVCOを直結した場合の一巡伝達関数
図3は位相検波器の検波感度を5[mA]/2π[rad]とし、組み合わせる積分用キャパシタを0.033μF、VCOの変調感度は第17話の図5と同じ100[kHz/V]としてExcelで伝達関数を計算したものです。位相検波器とVCOを直結するとフィードバック位相は全周波数で180°回転している事が判ります。これは二次ループが本質的に、入力変化のない状態では負帰還ループですが、少しでも変化があると正帰還になるという、恐ろしく不安定なフィードバックループであることを示しています。実際に閉ループ伝達関数を計算してみると、図4に示すように一巡伝達関数(利得)が0dBとなる周波数(極)で閉ループ利得が無限上昇、つまりループ発振する事が判ります。
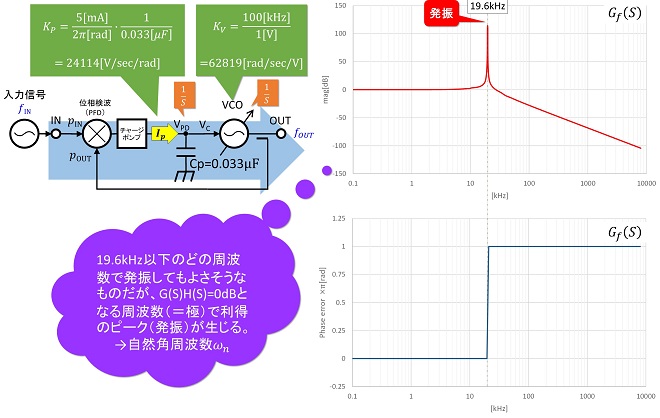
図4 定電流型チャージポンプとVCOを直結した場合の閉ループ伝達関数
ここで興味深いのは、全周波数に渡ってフィードバック位相は反転しているのに、ループ発振に至る周波数は一巡伝達関数G(S)H(S)=0dBとなる周波数、すなわち極の周波数だと云うことです。この周波数(角周波数)をループの自然角周波数ωnとも呼びます。発振回路の原理を学んだ人ならピンとくると思いますが、これはωnのみが「発振開始条件」と「発振持続条件」の両方を満足しており、それより低い周波数は「発振開始条件」のみ、高い周波数ではどちらも満足できない事が理由です。「発振」とは振幅が大きくなったり、小さくなったりを周期的に繰り返す事象です。入力角周波数がωnより小さい場合、ループの利得は>0dBなので、正帰還になるとループの信号レベルはどんどん上昇しようとしますが、止めどなく上昇して発散するため振動には至りません。逆に入力角周波数がωnより大きい場合はループの利得が<0dBなので、信号レベルがどんどん上昇することはありません。結果、信号レベルが上昇し、振動(発振)に至るのはループの利得が0dBであるωnのみとなります。
2. 不安定な高次ループを安定に使用する方法
昨今のPLL-ICを用いると、二次ループのPLLになるので、そのままではループ発振して使えないと言うことはお解り頂けたと思います。この不安定な二次ループを安定に使用するために必要になるのが「ループフィルタ」です。
(1) ループフィルタの種類
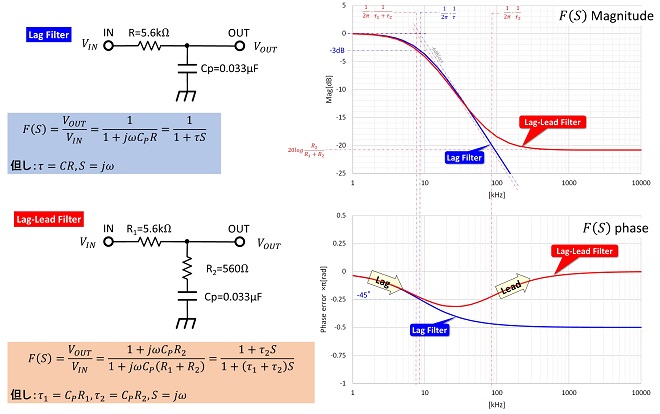
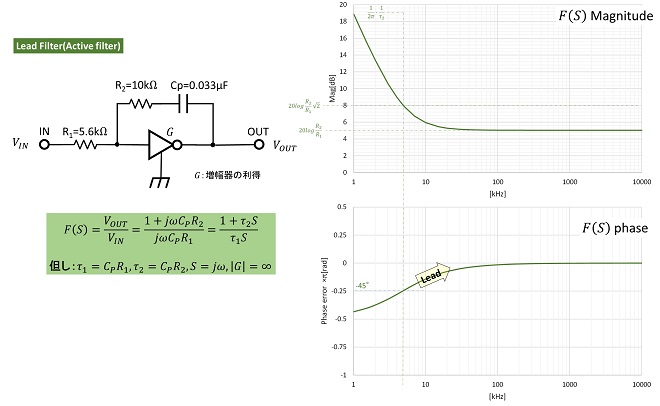
PLLの教科書に良く登場するループフィルタは図5に示す「ラグフィルタ」、「ラグリードフィルタ」ならびに図6に示す「リードフィルタ(アクティブフィルタ)」の3種類から選択、または組み合わせたものが一般的です。なお図5、図6に記載の通り、ループフィルタの伝達関数にも1/Sの項が含まれており、フィルタを挿入することでループの次数はさらに高次になります。
「ラグフィルタ」と「ラグリードフィルタ」はCRで構成されるパッシブLPFであり、カットオフ周波数前後で通過位相がπ[rad]遅れる特性を持ちます。
「リードフィルタ(アクティブフィルタ)」の場合は反転増幅器がベースなのでカットオフ周波数前後で位相がπ[rad]進みます。これらのフィルタの使い分けについては話すと長くなるので一旦専門書に譲ることにします。(このあと機会があれば書きます)
(2) ループフィルタの使い方
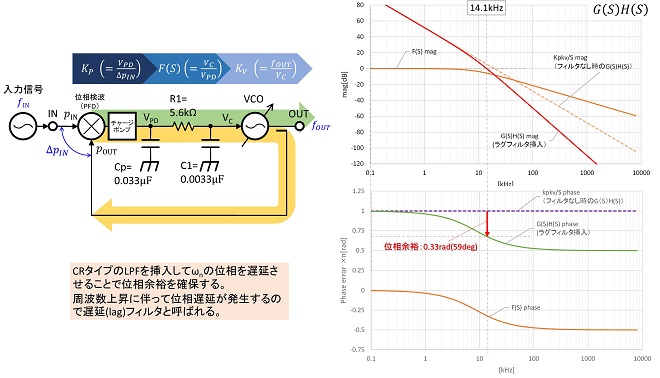
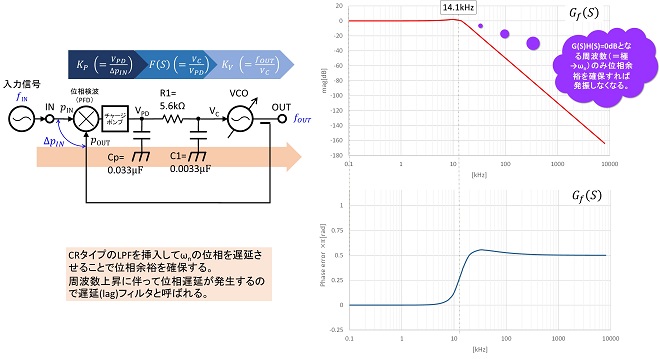
ループフィルタの有する位相遅れ/進みの特性を利用して一巡伝達関数(利得)が0dBとなる周波数での位相が±π[rad]にならないようにすれば、二次ループであってもループ発振を回避することができます。ちなみにこの操作は第16話で解説した「位相余裕」を確保する操作と同じです。最後に図4のPLLにラグフィルタを適用して位相余裕を確保した結果を図7,図8に示します。
図7は図5のループにこのループのωnよりも少し低いカットオフ周波数をもったラグフィルタを挿入した場合の一巡伝達関数G(S)H(S)の周波数対振幅/位相特性をグラフで示したものです。 ループフィルタを挿入することによりωnは19.6kHz→14.1kHzに低下、G(S)H(S)の位相特性は1kHz付近から徐々に遅れはじめますが、新しいωn(14.1kHz)では0.33radの位相余裕を確保できています。図8はこの時の閉ループ伝達関数です。
既にお気づきと思いますが、二次ループは全周波数においてG(S)H(S)の位相がπ[rad]遅延するのに対して、ラグフィルタで位相補正したのは、ループフィルタのカットオフ周波数より高周波側のみです。これは、図3、図4で解説した通り、周波数軸上のどこからループ発振が始まっても、最終的に発振が持続できるのはωnのみであるためです。周波数領域で見た時に、ωnで位相余裕が確保できていれば、時間領域で見た時に、何らかの入力変化でループが振動を始めても、その振動は持続できずに減衰し、結果ループは安定状態を維持することになります。
3. 第18話のまとめ
第18話では、一般に使用されているPLLが二次以上の高次ループとなること、ならびに高次ループはそのままでは不安定(発振する)であり、ループフィルタを挿入して極の周波数(固有角周波数ωn)の位相余裕を確保する必要があることを解説しました。以下、第18話の要点です。
- ①PLLはVCOの伝達関数に時間積分項が存在するので、ループフィルタを挿入すると必ず二次以上の高次ループとなる。
- ②特に定電流型チャージポンプを採用した最近のPLL-ICは、位相検波器の伝達関数にも時間積分項が存在するため、ループフィルタを挿入しない状態で二次ループとなっている。
- ③二次のループでは一巡伝達関数にπ[rad]の位相遅れが発生するため、定常状態(直流)が負帰還であっても入力変化(交流)に対して常に正帰還の状態となり、位相補正なしでループを閉じると、極の存在する周波数でループ発振する。この時の発振周波数(角周波数)を自然角周波数: ωnと呼ぶ。
- ④第16話で解説した「位相余裕」の確保は、実は自然角周波数: ωnにおいてのみ実施すれば良い。
フィードバック制御系の入力に変動(PLLの場合は位相のずれ)が発生すると、一次のループでは出力信号が誤差の大きさに応じて補正されることで、これに追従します。一方で高次のループでは入力に変動が発生すると、一旦ωnで発振(振動)し、それが減衰する過程で出力が入力の変動に追従します。高次のループは原理的に不安定なので、ループ設計の観点からすれば無理に採用することは避けたいと考えるのですが、この「一旦振動する」特性のおかげで、動的な追従特性が良くなります。次回はこのあたりを含めて解説を進めます。
また今回は原理的な部分にフォーカスしてラグフィルタを用いましたが、昨今の定電流型チャージポンプのアプリケーションではパッシブリードフィルタの適用が一般的ですので、次回はこのあたりにも少し触れておきたいと考えます。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)