今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第21話
ループフィルタとPLLの応答特性の話(その6)
2023年11月1日掲載
第16話から第20話まで、5回に渡りPLLのループフィルタの基本的な考え方について一通り解説しました。その中で「一次ループ」、「二次ループ」という言葉を多用してきました。ループフィルタのお話の最終回は、このループの次数について解説します。
1. ループの次数は入力変化に対する出力応答の違いを示す
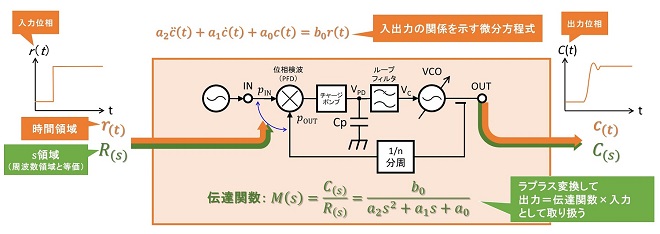
ループの次数というのは、正確には伝達関数の次数です。PLLのようなフィードバックシステムでは閉ループ伝達関数の次数と言うことになります。制御工学においては「一次遅れ」、「二次遅れ」という言葉で表現され、入力量の変化に出力量が追随する際の「遅れ方」の違いを表しています※1。→ 図1
図1において、PLLに周波数設定変更などの制御を行った時の入力r(t)の変化と出力応答c(t)の関係は微分方程式で表現され、一般化すると(式1-1)で示されます。
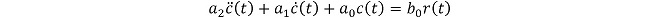
(式1-1)
この微分方程式を直接入出力の関係式に整理する(つまり微分方程式を解く)のは大変なので、「ラプラス変換というテクニックを使って解く」というのが大学の制御工学で学んだところでした。ということで、(式1-1)をt=0においては定常状態で、かつ0、すなわち c (0) = (0) = 0とおいてラプラス変換すると、
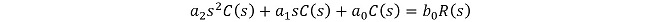
(式1-2)
これを入出力の関係式になるように整理すると
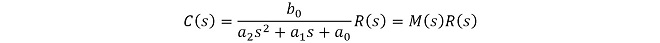
(式1-3)
を得ます。M(s)は伝達関数です(第16話参照)。このM(s)の分母の式の次数がループの次数です。従って伝達関数の一次、二次とは、時間領域において入出力特性を示す微分方程式が1階の微分方程式か、2階の微分方程式かを示していることになります。微分方程式の階数が変わるので挙動が変わるというのは察して頂けると思います。以下、具体的にどのように挙動が変わるのかについて解説します。
※1: 本項ではPLLのお話なのでフィードバックループに限定して解説しましたが、制御工学で言う一次遅れ、二次遅れというのは、機械や回路全般の挙動の遅延を示す概念で、フィードバックシステム以外にも適用されます。
2. 一次遅れ
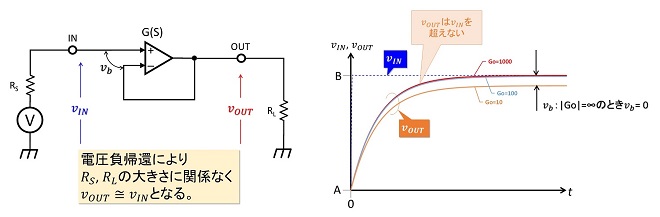
PLLは入力位相差に応じて出力の周波数を制御する構成をとるため、最初から積分項(1/S)が存在します。このためループフィルタを挿入すると、必ず二次遅れを有する系になってしまいます。電子回路において一次遅れの特性を示す代表的な回路としては、図2に示すオペアンプによるボルテージフォロワ回路が挙げられます。
一次系の応答特性(一般式)は(式2-1)に示す1階の線形微分方程式で表現されます。
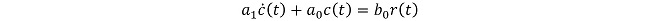
(式2-1)
伝達関数は(式2-1)を(式1-2)と同じ考え方でラプラス変換した後、入出力の関係式に整理することで得られ、(式2-2)となります。
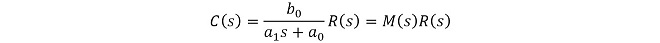
(式2-2)
ボルテージフォロワ回路の場合は(式2-2)を(式2-3)のように変形して適用します。
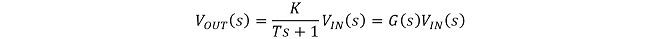

K : ボルテージフォロワの直流利得
G0 : オペアンプの直流開ループ利得
T : オペアンプの時定数(遅延時間)
(式2-3)
この回路のステップ応答特性、すなわち入力電圧VINがt=0でA → Bにステップアップ(またはダウン)したときの出力電圧VOUTの時間変化は図2の右のグラフに示すような特性になります。
一次系は、フィードバック信号の位相がループの遅延のみで決定される系であり、フィードバック信号の位相反転が起きる周波数において開ループ利得が1以下であれば、発振することも振動する事もなく常に安定です。ステップ応答において、出力電圧VOUTは限りなくVINに漸近しますが常に一定量の定常誤差が発生します。この定常誤差はオペアンプが電圧を出力する為に必要な入力電圧vbに相当し、オペアンプの開ループ利得 G0=∞の時、vb=0Vとなります。
3. 二次遅れ
2項で触れた通り、PLLはその構成から基本的に二次以上の次数の応答特性になります。二次系の応答特性(一般式)は(式3-1)に示す2階の線形微分方程式で表現されます。
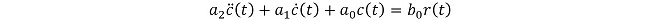
(式3-1)
伝達関数は(式3-1)のラプラス変換から(式3-2)となります。
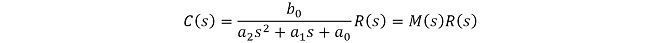
(式3-2)
PLLにおいては(式3-2)を(式3-3)のように変形して適用します。
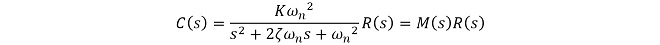
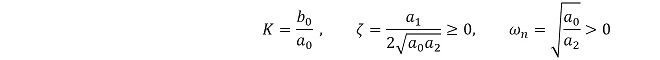
K:閉ループ利得の直流項、ζ:減衰定数、ωn:固有角周波数(または自然角周波数)
(式3-3)
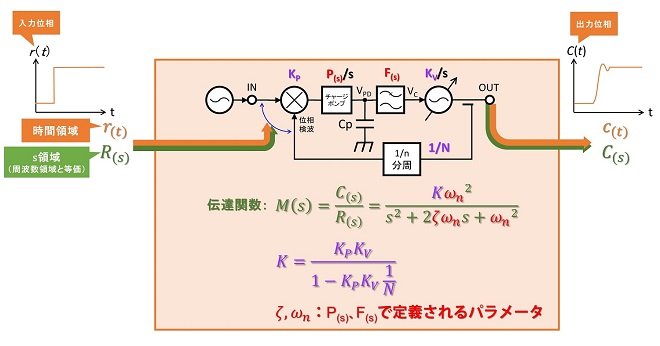
これらの関係を図3に整理しておきます。
この回路のステップ応答特性、すなわち入力信号の位相R(s)がt=0でA[rad] → B[rad]にステップアップ(またはダウン)したときの出力信号の位相C(s)の時間変化は図4に示すような特性になります。
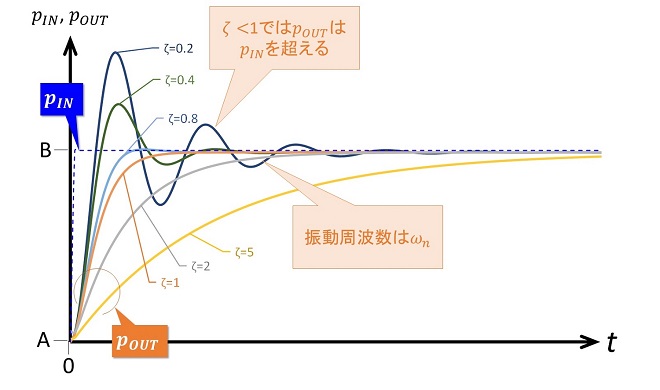
図4 二次ループPLLのステップ応答特性
二次系のループはフィードバック信号に積分要素が含まれていて、周波数領域で見ると常に位相が反転している系です。定常状態(0Hz)ではネガティブフィードバックの状態になるので安定ですが、ひとたび入力に変化が発生するとループが振動します。第18話で解説した通り、この時の振動周波数が固有角周波数ωnです。振動の大きさは減衰定数ζの大きさによって以下のように変化します。
- ζ=0: 持続振動(発振状態)となる。
- 0 ≤ ζ < 1: 応答が振動する。ζの値が大きい程、振動は早く減衰する。
- ζ≤1: 応答は振動しない。
二次のループではこのような振動特性があるため、入力の変化に対して、出力の「行き過ぎ」が発生します。図3においてωnとζはチャージポンプの伝達関数P(s)とフィルタの伝達関数F(s)で定義されると書きました。実際にどのように導出されるのか、第19話の図4、図5で解説した定電流型チャージポンプの伝達関数からωnとζを導出してみます。
まず位相検波器の利得Kpをチャージポンプの積分項と分離できる形に整理します。
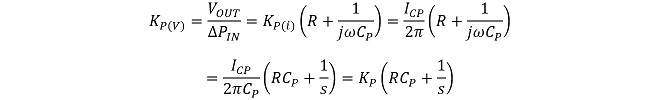
(式3-4)
整理したKpとVCOの変換利得Kvを用いて一巡伝達関数G(s)H(s)を求めます※2。
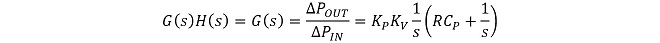
(式3-5)
(式3-5)から閉ループ伝達関数M(s)を導出。
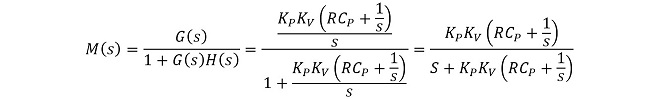
(式3-6)
M(s)の分母をs2 + 2ζωns + ωn2の形に整理して、ωnとζを導出する。
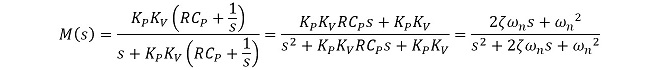
(式3-7)
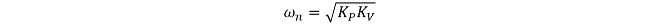
(式3-8)
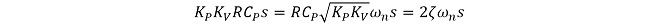
(式3-9)
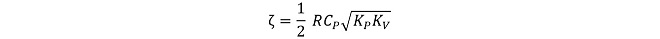
(式3-10)
ここでは位相検波器KPを整理する際に、チャージポンプの伝達関数の一部をKPに組み入れてしまったので、固有角周波数ωnがKpとKVだけで決定される整理となってしまいましたが、実際にはチャージポンプの応答が含まれています。→ (式3-4)参照
※2:H(s)=![]() (フィードバック系に分周数Nの分周器が挿入されている)の場合は以下の通りとなります。
(フィードバック系に分周数Nの分周器が挿入されている)の場合は以下の通りとなります。
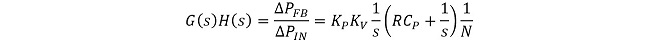
(式3-11)
(式3-11)から閉ループ伝達関数M(s)を導出。
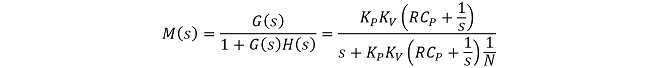
(式3-12)
M(s)の分母をs2 + 2ζωns + ωn2の形に整理して、ωnとζを導出する。
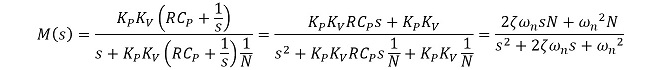
(式3-13)
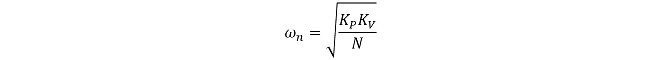
(式3-14)
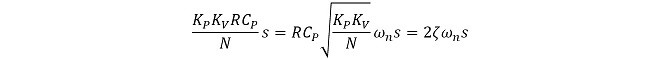
(式3-15)
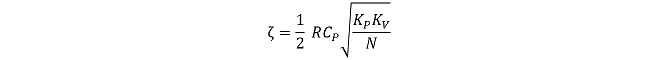
(式3-16)
4. 三次遅れ
三次以上の次数を持つ系の応答特性は二次の応答と一次の応答の組み合わせ(伝達関数の積)で表現されます。従って二次以上のループにおいてもステップ応答を見ると、二次ループと同様の振動特性を示します。二次ループと三次ループの違いはステップ応答ではなく、ランプ応答特性に表れます。位相のランプ応答とは入力位相があるタイミングを境に連続的に進む(または遅れる)変化をしたときの出力位相の追従特性です。つまり周波数をステップ変化させた時の応答特性になります。二次ループのPLLでは入力周波数をステップ(分周カウンタの分周数を変化させて周波数を切り替えた時に該当)させて、位相が連続的に進む(遅れる)状態になると、図5に示すように一定の追従誤差が発生します。この位相誤差は位相の増加速度Vと一巡伝達関数の定数部分K(=KP・KV/N)で決まります(位相差は一定値を保つので周波数偏差は生じません)。これに対して三次ループのPLLは周波数ステップに対する応答でも、このような位相誤差は発生しません。昨今PLLの主流が二次ループから三次ループになっているのはこの為かもしれません。
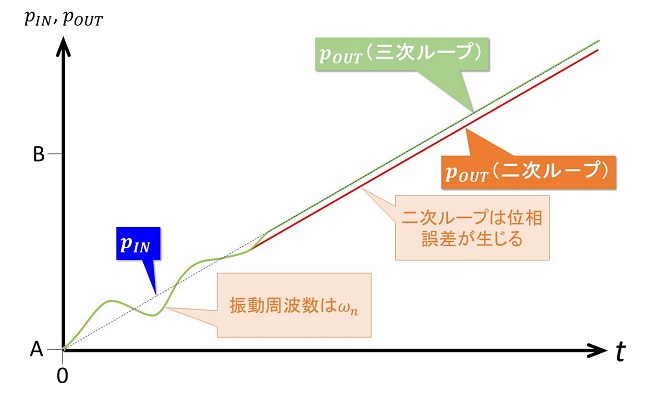
図5 位相ランプ(周波数ステップ)応答特性
5. 時間応答特性と位相余裕・利得余裕の関係
固有角周波数ωnは第20話までで解説した通り、ボードチャート(伝達関数の周波数特性図)上で、極として把握することができます。ζは位相余裕と関係しており、位相余裕を大きく採るほどのζの値は大きくなります。無線通信用のPLLにおいては出力信号の位相雑音特性が最も優先されるため、ωnとζを決めてからループ諸元を決定する手順は踏まず、位相雑音性能を決定するループ帯域を優先して位相余裕との妥協点を探す設計を行います。その後、時間応答特性をシミュレーションで確認するのが一般的です。
6. 第21話のまとめ
第21話ではPLLの時間応答特性について解説しました。昨今では回路シミュレータ以外にPLL専用のデザインシミュレータがPLL-ICメーカから提供される時代ですので、時間応答特性を解析的に求めるという設計を行う機会は減ったと思います。しかしPLL回路の次数を利用目的に合わせて選定する為には、フィードバックループの次数と時間応答特性の関係は理解しておく必要が有ります。表5-1にループの次数と応答特性の関係を整理しておきます。
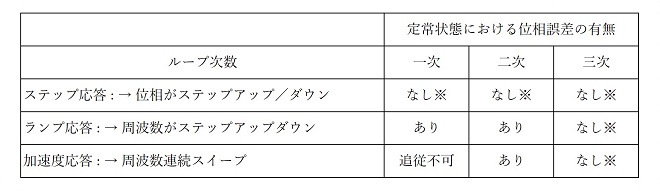
表5-1 ループ伝達関数の次数と各種入力変動に対する応答特性(定常誤差)
※利得が充分に大きい場合
ここで「追従不可」というのは、定常誤差がどんどん増加して同期できなくなる状態を示します。特に周波数を時間掃引(スイープ)するシンセサイザに適用するPLLの場合などは、三次ループで設計する事が重要になってきます。
PLLのお話はここまでで一区切りです。次回からは再び三角関数の掛け算の話に戻って、同一周波数の掛け算その2 周波数逓倍のお話です。
第21話の執筆には下記文献/URLを参考にさせて頂きました。
小沢利行著 PLLシンセサイザ・回路設計法 1994 総合電子出版社
制御工学の入門記事一覧 | こんとろラボ (controlabo.com)
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)