今更聞けない無線と回路設計の話
【テーマ1】三角関数のかけ算と無線工学
第3話 ミキサの線形性って何?
第2話ではトランジスタミキサ回路の動作原理について解説しましたが、一通りご説明した後で「ダイナミックレンジが小さいので最近ではあまり使われない」と申し上げました。高周波アナログ回路においてミキサは代表的な非線形回路ですが、そのミキサには線形性が要求されます。第3話では非線形回路に要求される線形性について解説します。
1. 周波数変換回路に要求される機能
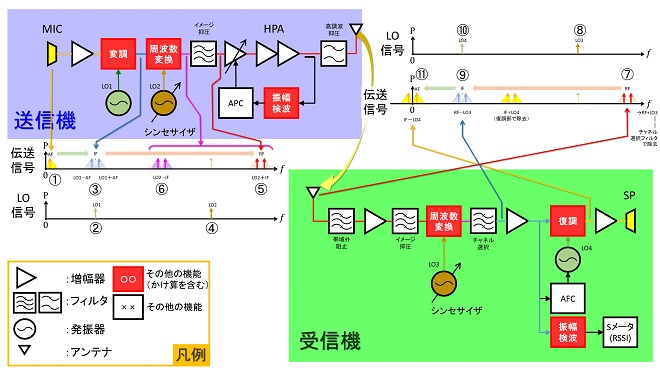
図1は無線通信機で周波数変換がどのように使われているかを説明する為に第一話の図1から「送信機」と「受信機」の部分を抜粋したものです。無線従事者免許を取得された方なら、図を見ればご理解頂けると思いますが、無線通信機において周波数変換回路は変調器の出力信号を無線送信周波数に変換、あるいは受信信号の周波数を復調器入力周波数に変換する機能を担います。
変調器の出力信号や、復調器に入力する信号は通信機として伝送する「伝送信号」であり、その元はマイクロホンで変換された音声信号などです。
私たちが発する音声は空気の振動(波)ですが、これをマイクロホンが電気信号に変換すると、図2に示すようにある帯域幅を持った信号になります。つまり様々な周波数のサイン波の集合体です。ちなみに図2は本連載第一話の冒頭の文章を音声合成ツールVOICEVOX※1で音声信号に変換し、音声編集ツールAudacity®※2でスペクトル解析したものです。(余談ですが、こんなことがフリーソフトで手軽にできてしまう時代になったのだなあ...と感慨にふけっています)

図2 音声信号(クリックして再生)のスペクトル※1、※2

話を図1に戻して、送信機の左端「MIC」と書かれたブロックの出力が図2のようなスペクトルになるので、図1のスペクトル分布を示すグラフ上では三角形で表しています(図中①、以下(①)と表記)。ここでは変調処理が単純な乗算であるDSB変調のスペクトル例を示しました。最初に変調部で音声伝送信号(①)にLO1信号(②)を掛け算すると(①)と(②)の和周波成分と差周波成分のスペクトル(③)が生成されます。この和周波成分と差周波成分の片方だけを伝送する方式がSSB(Single Side Band)方式、両方とも伝送する方式がDSB(Double Side Band)方式です。LO1信号は送信周波数ではないので、中間周波数(IF: Intermediate Frequency)信号と呼ばれます。
生成されたIF信号のスペクトル(③)は(①)のスペクトル群がLO1信号(②)に対して線対称に並んだ形になります(LO1スペクトルは乗算すると消えます)。次段の周波数変換部では、この信号に周波数がRF-IFのLO2信号(④)を掛け算します。周波数変換部の出力にはIF信号(③)のスペクトルとLO2信号(④)の周波数の和周波成分(⑤)と差周波成分(⑥)が生成され、次段のイメージ抑圧BPFで和周波成分(⑤)のみを濾波して送信信号RFとしています。
受信側では周波数変換部で受信信号RFのスペクトル(⑦)に周波数がRF-IFのLO3信号(⑧)を掛け算してIF信号(⑨)を生成。復調部でIF信号(⑨)に再生クロックLO4信号(⑩)を掛け算することで、元の音声信号(⑪)を得ています。
ここで着目して頂きたいのは、送受信される伝送信号は1本のサイン波ではなく、ある帯域幅をもったサイン波の集合体ということです。
通信機においては、このサイン波の集合体に別のサイン波(LO信号)を掛け合わせて周波数変換し、電波として伝送するのですが、受信側で同様に処理して元の周波数に戻した時、その集合体の中身(スペクトル分布)は、当然元の集合体と同じ構成でなければ、通信機としての役割を果たせません。
つまり周波数変換回路には、帯域を持った信号のスペクトル分布を維持したまま、所望の周波数にシフトさせる特性が要求されるのです。
2. 実はf1×f2ではない
この特性を実現するためには、伝送信号とLOをどのように掛け算する必要があるかというと、

(式2-1)
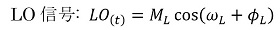
(式2-2)
としたとき、乗算回路の出力y(t)は
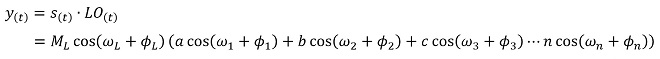
(式2-3)
但しa,b,c... : 伝送信号を構成する各周波数スペクトルの振幅
ω1,ω2...ωn : 伝送信号スペクトルを構成する各角周波数[rad/sec]
ϕ1,ϕ2...ϕn : 伝送信号を構成する各周波数スペクトルの位相
ML: LO信号の振幅、ωL: LO信号の角周波数、ϕL: LO信号の位相
という掛け算になる必要があります。
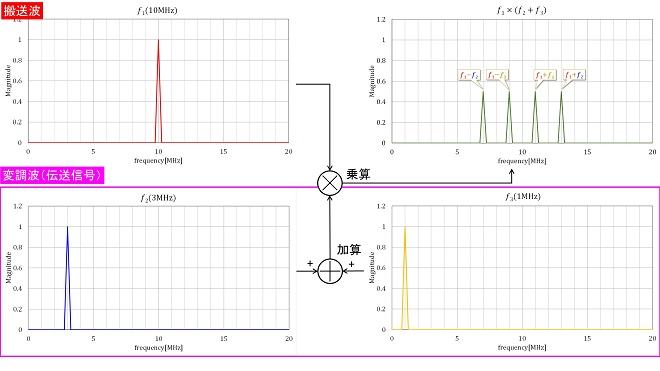
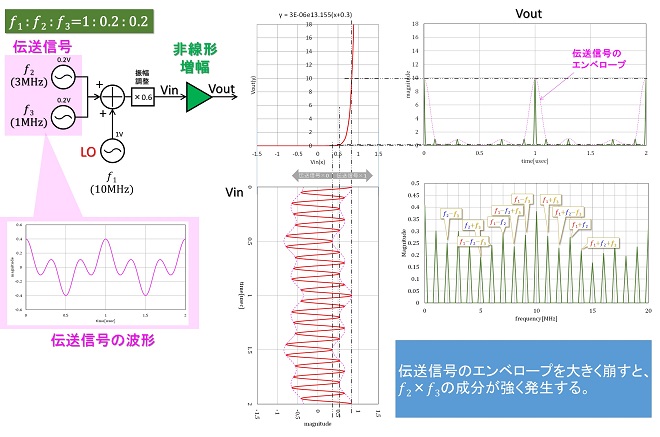
平たく言うと、伝送信号が周波数𝑓2と周波数𝑓3の2つの正弦波の合波信号、LO信号が周波数𝑓1だったとき、周波数変換回路で行う掛け算は𝑓1×(𝑓2+𝑓3 )である必要があります。(図3)
第2話の図4、図5で解説したミキサ回路は、掛け算する信号を混ぜ合わせて(足し算して)から非線形増幅を行うという動作原理でした。非線形増幅回路は入力された全ての信号を掛け算してしまうので、これに𝑓1,𝑓2,𝑓3の3つの正弦波の合成信号を入力すると、図3に示したような演算にならず、図4に示すような演算(全部掛け算される)になってしまい伝送信号が潰れてしまいます。実際の周波数変換回路では、この問題をどのように解決しているのでしょうか。
3. 非線形回路でf1×(f2+f3)を実現する方法
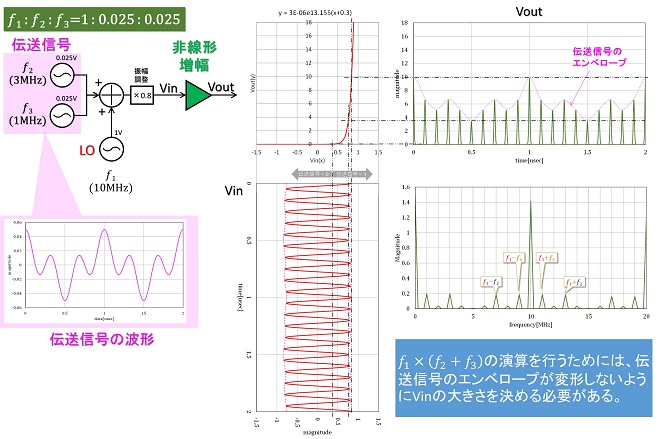
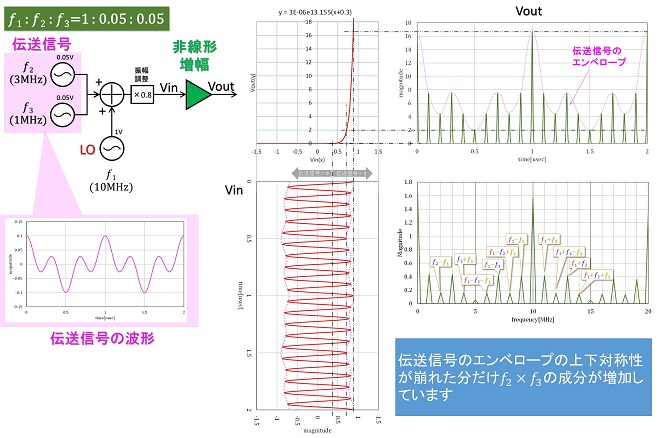
実際の周波数変換回路では、伝送信号のスペクトル同士が掛け算されることを防ぐために、LOと伝送信号の間に大きなレベル差(振幅差)を設けています。伝送信号とLOのレベル差が掛け算処理にどう関係するのかを図5~図7を使って解説します。伝送信号は様々な周波数のサイン波が様々な位相差で合成された信号なので複雑な波形になります。図5~図7では図3,図4と同様、𝑓2=3MHz,𝑓3=1MHzの所謂2トーン信号を例にしていますが、図5~図7の左側の吹き出しに示したように、2波であっても時間波形は複雑な振幅になります。LO信号𝑓1が伝送信号𝑓2+𝑓3よりも大振幅であれば、非線形増幅の出力信号のエンベロープには伝送信号波形の形が現れます。このエンベロープの形が伝送波形に近ければ近いほど、出力波形は𝑓1×(𝑓2+𝑓3 )に近く(図5)、エンベロープに現れる伝送波形の形状が歪んでいるほど、出力波形は𝑓1×𝑓2×𝑓3に近づきます(図6~7)。Vin波形に現れる伝送信号の振幅が、非線形増幅器の非線形性の強い領域にかからないように、LO信号の振幅がバイアスの機能を果たしていることが、図5のグラフからお解り頂けると思います。これがLO信号の振幅が大きいと出力エンベロープが伝送波形に近づく理由です。
周波数変換回路の線形性とは、伝送信号を構成するスペクトル同士を掛け算してしまう事がどれだけ少ないかと言うことであり、出力信号のエンベロープに現れる伝送信号の波形がどれだけ歪まないかで決まります。
4. 第3話のまとめ
第3話では周波数変換回路に要求される特性を掘り下げて解説しました。以下、要点を整理します。
- ① 周波数変換回路で取り扱う伝送信号は周波数帯域幅を有する信号(周波数が異なる複数のサイン波の集合体)である。
- ② 伝送信号の情報を崩さずに周波数変換を行うためには、伝送信号のスペクトル相互が掛け算されないようにする必要がある。
- ③ ②をアナログミキサで実現するためには、LO>伝送信号の関係を保ち、増幅器の非線形特性領域が直接伝送信号振幅に影響しないようにする必要がある。
次回も引き続き、図5~図7、ならびに回路シミュレータを用いて、トランジスタミキサが行う掛け算と周波数変換回路の直線性について、さらに深掘りしてみたいと思います。
※1: VOICEVOX © 2021 Hiroshiba Kazuyuki の詳細は下記URLを参照ください。
https://voicevox.hiroshiba.jp/
※2: Audacity® の詳細は下記URLを参照ください。
https://www.audacityteam.org/
※3: 図3、図4の作図に用いたExcel※4シートはここからダウンロードできます。なおダウンロードされたExcelシートに関するご質問についてはご容赦ください。これらExcelシートの内容に関する知的財産権その他一切の権利は筆者濱田倫一に帰属します。月刊FB NEWS編集部は筆者濱田倫一の許可を得て本件記事を掲載しております。また筆者、ならびに月刊FB NEWS編集部は、これらExcelシートの二次使用に伴う一切の責任を負いませんので、あらかじめご了承ください。
※4: Excelは米国マイクロソフト社の商標です。
今更聞けない無線と回路設計の話 バックナンバー
- 【テーマ2】デシベルと無線工学 (第17話) レベルダイヤグラムの縦軸(その1)
- 【テーマ2】デシベルと無線工学 (第16話) レベルダイヤグラムの構成
- 【テーマ2】デシベルと無線工学 (第15話) 非線形歪み(その5)
- 【テーマ2】デシベルと無線工学 (第14話) 非線形歪み(その4)
- 【テーマ2】デシベルと無線工学 (第13話) 非線形歪み(その3)
- 【テーマ2】デシベルと無線工学 (第12話) 非線形歪み(その2)
- 【テーマ2】デシベルと無線工学 (第11話) 非線形歪み(その1)
- 【テーマ2】デシベルと無線工学 (第10話) 線形歪み(フェージング現象)
- 【テーマ2】デシベルと無線工学 (第9話) 足される雑音と掛けられる雑音
- 【テーマ2】デシベルと無線工学 (第8話) 等価雑音の内訳
- 【テーマ2】デシベルと無線工学 (第7話) 無線通信の成立条件(その3)
- 【テーマ2】デシベルと無線工学 (第6話) 無線通信の成立条件(その2)
- 【テーマ2】デシベルと無線工学 (第5話) 無線通信の成立条件
- 【テーマ2】デシベルと無線工学 (第4話) dBmとdBµVの複雑な関係
- 【テーマ2】デシベルと無線工学 (第3話) dB(デシベル)を知る(その2)
- 【テーマ2】デシベルと無線工学 (第2話) dB(デシベル)を知る(その1)
- 【テーマ2】デシベルと無線工学 (第1話) (プロローグ)無線通信機の天井と床
- 【テーマ1】三角関数のかけ算と無線工学 (第30話) 三角関数のかけ算と無線工学の切っても切れない深い縁
- 【テーマ1】三角関数のかけ算と無線工学 (第29話) 交流ベクトル空間と直交ミキサ(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第28話) 交流ベクトル空間と直交ミキサ(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第27話) 交流ベクトル空間と直交ミキサ(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第26話) 交流ベクトル空間と直交ミキサ
- 【テーマ1】三角関数のかけ算と無線工学 (第25話) マイナスの周波数
- 【テーマ1】三角関数のかけ算と無線工学 (第24話) 同一周波数のサイン波の掛け算と周波数の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第23話) 同一周波数のサイン波の掛け算と周波数の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第22話) 同一周波数のサイン波の掛け算と周波数の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第21話) ループフィルタとPLLの応答特性の話(その6)
- 【テーマ1】三角関数のかけ算と無線工学 (第20話) ループフィルタとPLLの応答特性の話(その5)
- 【テーマ1】三角関数のかけ算と無線工学 (第19話) ループフィルタとPLLの応答特性の話(その4)
- 【テーマ1】三角関数のかけ算と無線工学 (第18話) ループフィルタとPLLの応答特性の話(その3)
- 【テーマ1】三角関数のかけ算と無線工学 (第17話) ループフィルタとPLLの応答特性の話(その2)
- 【テーマ1】三角関数のかけ算と無線工学 (第16話) ループフィルタとPLLの応答特性の話(その1)
- 【テーマ1】三角関数のかけ算と無線工学 (第15話) 位相検波器の話
- 【テーマ1】三角関数のかけ算と無線工学 (第14話) PLLの動作原理と代表構成
- 【テーマ1】三角関数のかけ算と無線工学 (第13話) PLLの役割とサイン波の純度について
- 【テーマ1】三角関数のかけ算と無線工学 (第12話) 同一周波数のサイン波のかけ算と位相のはなし
- 【テーマ1】三角関数のかけ算と無線工学 (第11話) ギルバートセル乗算器(その3・ギルバートセル乗算回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第10話) ギルバートセル乗算器(その2・定電流源とカレントミラー回路)
- 【テーマ1】三角関数のかけ算と無線工学 (第9話) ギルバートセル乗算器(その1・差動増幅の基礎)
- 【テーマ1】三角関数のかけ算と無線工学 (第8話) ダブルバランスドミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第7話) ダブルバランスドミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第6話) トランジスタミキサ②
- 【テーマ1】三角関数のかけ算と無線工学 (第5話) トランジスタミキサ①
- 【テーマ1】三角関数のかけ算と無線工学 (第4話) 非線形動作を利用したかけ算のまとめ
- 【テーマ1】三角関数のかけ算と無線工学 (第3話) ミキサの線形性って何?
- 【テーマ1】三角関数のかけ算と無線工学 (第2話) 周波数変換とミキサ(混合)回路
- 【テーマ1】三角関数のかけ算と無線工学 (第1話) サイン波のかけ算
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定