Mr. Smithとインピーダンスマッチングの話／【第3話】スミスチャートとは何か（その1）｜2019年1月号

Mr. Smithとインピーダンスマッチングの話

【第3話】スミスチャートとは何か（その1）

濱田倫一

第2話ではインピーダンス変換とは何か？とインピーダンス整合回路の設計について、スミスチャートの意味合いは後回しにしてMr. Smithを使いながら解説しました。今月はスミスチャートの目盛りの読み方を中心に解説しようと思いますが、タイトルに“その1”とあるように、「スミスチャートとは何か」の核心に触れるお話はもう少し先でさせていただきたいと考えます。

スミスチャートのあの奇妙な目盛りは反射係数とインピーダンスの関係を示すものなのですが、反射係数の解説を先にするとそれだけでお腹一杯になってしまうと思いますので、第3話ではレジスタンス（R）、リアクタンス（jX）、コンダクタンス（G）、サセプタンス（jB）、ならびにインダクタンス（L）、キャパシタンス（C）とチャートの関係に絞って解説します。

1. スミスチャートの読み方

この章でお話しする内容は伝送線路上の電源と負荷の関係、特に反射係数Γについての知識がないと完全に理解することができません。これらについては後日改めて触れますので、反射係数や特性インピーダンスの話がイマイチ消化不良でも、第3話では「そういうものだ」程度で理解しておいてください。図１に我々が入手可能なスミスチャートの例を示します。左のチャートはグラフ用紙でおなじみの「Tochiman」ブランドから販売されているもので、今でも図に示したURLから購入可能です。（筆者も昔は愛用していました）右は.png形式の画像ファイルのスミスチャートで1024×1024の解像度があります。図に示したURLから無料でダウンロードできます。第3話はこのチャートを使用させて頂きました。

図１　スミスチャート（左：市販のグラフ用紙※１、　右：画像ファイル（フリー）※２）
※１　https://www.sakaetp.co.jp/shop/products/detail.php?product_id=51
※２　https://www.kisspng.com/png-smith-chart-with-scale-full-color-stub-electrical-798866/

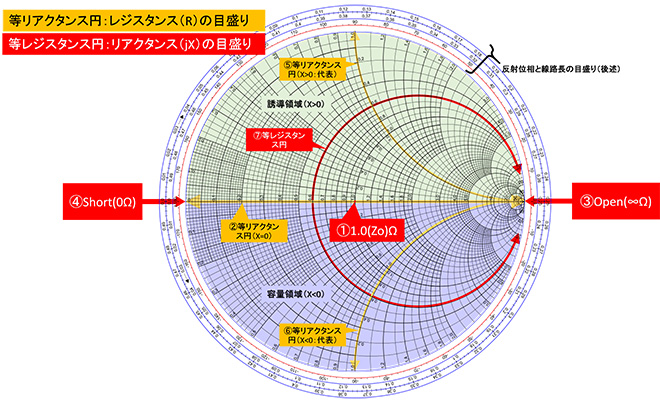
図2にスミスチャートのインピーダンス目盛りの説明を示します。最外周の反射位相と線路長の目盛りについては第3話では省略します。第3話で理解して頂きたいのは赤とオレンジで示した部分です。

図2　スミスチャート（インピーダンスチャート）の読み方

(1)スミスチャートの目盛りは正規化インピーダンス
スミスチャートとは「伝送線路の反射係数とインピーダンス値を関連付けたチャート」です。このためスミスチャートのインピーダンス目盛りは扱う線路の特性インピーダンスZo（または整合設計を行う際の基準インピーダンス）で正規化（Z/Zo）して表示されています。図2に①で示す通りチャートの中心は「1.0」と書かれており、ここをZo[Ω]と読み替えることになります。

何故チャートの中心がZo[Ω]なのかについては第五話あたりでお話します。一般的に高周波系の測定器の入出力インピーダンス、同軸ケーブル、コネクタ類は50Ωで設計されている場合が多いことから、スミスチャートもZo=50Ωとして取り扱うことが多いので、スミスチャートの中心は50Ωだと思い込んでいる人を見かけますが正しくはZoです。Mr. Smithでは起動画面でZoの値を設定することで正規化計算を自動的に処理しています（→第二話の図２を参照）。なお単純にインピーダンスとアドミッタンスの接続計算のみを行う場合は、Zoは物理的な意味を持ちませんが、実際に計算するインピーダンスの絶対値から大きく離れた値にすると目盛りの読み取り精度が悪くなります。

(2)直列Rの目盛り：等リアクタンス円
図2においてオレンジの矢印と吹き出しで示した放射状の目盛りが等リアクタンス円です。「円ではないじゃないか」というご意見も出そうですが、チャートの外側に中心がある大きな円の一部です。ちなみにチャートの外側も負性抵抗領域として意味のある領域ですが、今は割愛します。

まずチャートの中央を左右に貫くライン（図2の②）がjX=0Ωの目盛りつまり純抵抗のラインとなります。右端（③）が∞Ω（Open）、左端（④）が0Ω（Short）で直列に抵抗Rを接続するとインピーダンスはこの目盛り上を右に移動してゆきます。何がしかのリアクタンス成分（jX）が接続された状態のときは上下に広がる目盛り上にプロットされます。この時、誘導性リアクタンス（Lが直列接続されている→ +jX）の場合は⑤（代表）で示す上半分の目盛り、容量性リアクタンス（Cが直列接続されている→-jX）の場合は⑥（代表）で示す下半分の目盛り上にプロットされます。そしてR+jXΩのインピーダンスに直列にRを接続すると、合成インピーダンスはこの等リアクタンス目盛り上を③の∞Ωの方向に向かって移動してゆきます。この動きはMr. Smithで簡単に確認することができます。→図３参照

(3)直列ｊXの目盛り：等レジスタンス円
図2において赤の矢印と吹き出しで示したOpenの点（図2の③）に接する円形の目盛り⑦(代表)が等レジスタンス円です。この目盛りはjX=0Ωの目盛り（図2の②）と接する点が0Ωで、上半分が+jX、下半分が-jXの正規化リアクタンス（jX/Zo）を示し、時計回りに値が大きくなります。＋側と－側はOpen（図2の③）の点でそれぞれ+j∞Ω、-j∞Ωとなって合流します。

R+jXΩのインピーダンスに誘導性リアクタンス（+jX）（＝L）を直列接続すると合成インピーダンスは等レジスタンス円上を時計方向に、容量性リアクタンス（-jX）（＝C）を直列接続したときは等レジスタンス円上を反時計方向に移動します。→図4参照。

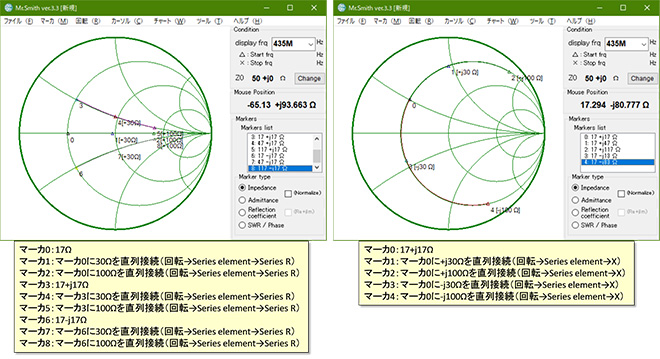
左：図3　直列Rを接続したときの動き　右：図4　直列jXを接続したときの動き

(4)インピーダンスを並列接続したときの動き
次にR+jXΩにあるインピーダンスを並列接続したときのチャート上の動きを説明します。R+jXΩに別のインピーダンスを並列接続したときの合成インピーダンスは、スミスチャートの目盛り上を移動しません。並列接続したときの合成インピーダンスは図5に示すようにチャートを左右反転した目盛りに沿って変化します。この左右反転したチャートの事をアドミッタンスチャートと呼びます。これに対して(1)～(3)で説明してきたチャートの事をインピーダンスチャートと呼びます。一般に「スミスチャート」というと、インピーダンスチャートの事を示す場合が多いですが、実際にはインピーダンスチャート／アドミッタンスチャートをセットで使用します。

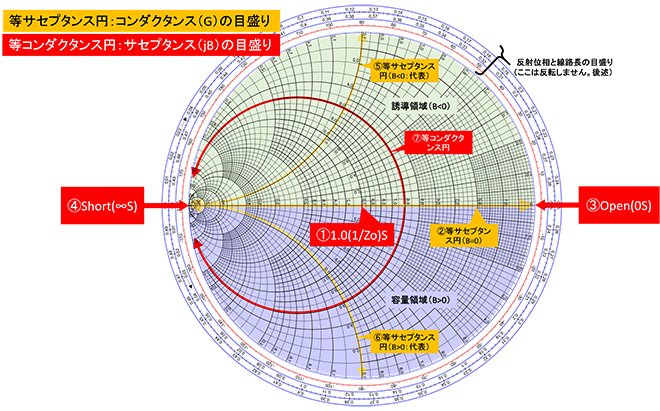
アドミッタンスチャートの目盛りもインピーダンスチャートと同様、正規化アドミッタンス（Y/Yo=Y･Zo）で表示されており、チャートの中心（図5の①）は1.0と書かれており、ここを1/Zo[S]と読み替えることになります。インピーダンスチャートとアドミッタンスチャートはそれぞれ反射係数Γの値と正規化インピーダンス、正規化アドミッタンスの関係をプロットしたチャートなので、Zo[Ω]と1/Zo[S]の点（図2、図5の①）、Openの点（図2、図5の③）、Shortの点（図2、図5の④）を一致させる形で重ね合わせることができます。つまりインピーダンスチャート上にプロットされたR+jX[Ω]の点をアドミッタンスチャートの目盛りで読めばアドミタンスへの換算値（G+jB＝1/(R+jX)[S]）を得ることができます。インピーダンスチャートとアドミッタンスチャートを最初から重ね合わせた「イミッタンスチャート：Immittance chart」もありますが、目盛りが細かくなりすぎて読み取りづらいので、筆者はインピーダンスチャートとアドミッタンスチャートを交互に使用しています。

図5　アドミッタンスチャートの読み方

(5)並列R（直列G）の目盛り：等サセプタンス円
図5においてオレンジの矢印と吹き出しで示した放射状の目盛りが等サセプタンス円です。まずチャートの中央を左右に貫くライン（図5の②）がjB=0Sの目盛り、つまり純抵抗のラインとなります。右端（③）が0S（Open）、左端（④）が∞S（Short）で、並列に抵抗Rを接続（すなわち直列にGを接続）するとアドミッタンスはこの目盛り上を左に移動してゆきます。何がしかのサセプタンス成分（jB=1/(jX)）が接続された状態のときは上下に広がる目盛り上にプロットされます。この時、誘導性サセプタンス（Lが並列接続されている→ -jB）の場合は⑤（代表）で示す上半分の目盛り、容量性サセプタンス（Cが並列接続されている→+jB）の場合は⑥（代表）で示す下半分の目盛り上にプロットされます。そしてR+jXΩのインピーダンスに並列にRを接続（すなわちG+jBのアドミッタンスに直列にGを接続）すると、合成アドミッタンスはこの等リアクタンス目盛り上を④の∞Sの方向に向かって移動してゆきます。この動きはMr. Smithで簡単に確認することができます。→図6参照

(6)並列ｊX（直列ｊB）の目盛り　：等コンダクタンス円
図5において赤の矢印と吹き出しで示したShortの点（図5の④）に接する円形の目盛り⑦(代表)が等コンダクタンス円です。この目盛りはjB=0Sの目盛り（図5の②）と接する点が0Sで、上半分が-jB、下半分が+jBの正規化リアクタンス（jB/Yo = jB･Zo）を示し、時計回りに値が大きくなります。＋側と－側はShort（図5の④）の点でそれぞれ+j∞S、-j∞Sとなって合流します。

R+jXΩのインピーダンスに誘導性リアクタンス（+jX）（＝L）を並列接続（すなわちG+jB[S]のアドミッタンスに誘導性サセプタンス（-jB）を直列接続）すると合成アドミッタンスは等コンダクタンス円上を反時計方向に、容量性リアクタンス（-jX）（＝C）を並列接続（すなわち容量性サセプタンス（+jB）を直列接続）したときは等コンダクタンス円上を時計方向に移動します。→図7参照。

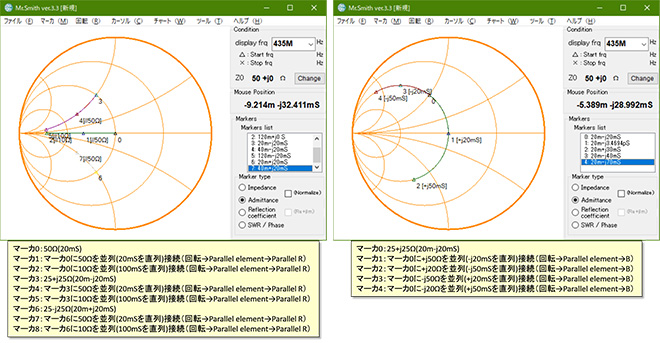
左：図6　並列R（直列G）を接続したときの動き　右：図7　並列jX（直列jB）を接続したときの動き
（Mr.Smithでアドミッタンスチャートを表示するにはチャートメニューから選択します。）

2. 第2話の振り返り

スミスチャートの読み方について理解して頂いたので、もう一度第2話の【練習問題2】を振り返ってみましょう。

【練習問題2】
周波数435MHz、出力インピーダンス50ΩのSGの出力を75Ωの同軸ケーブルに接続するためのインピーダンス変換回路を設計せよ。

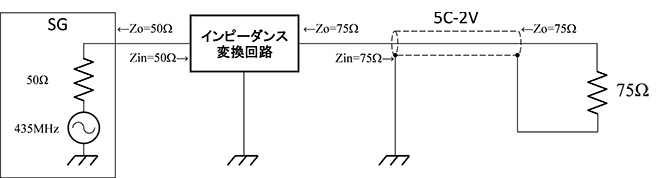
図8　練習問題2（第2話から再掲）

第3話では第二話と同じ設計を普通のスミスチャートで解いてみましょう。第二話で述べた通り負荷インピーダンス（75Ω）を電源インピーダンス（50＋j0Ωの共役=50Ω）に変換する計算です。直並列接続を行いますので、イミッタンスチャートを使用するか、またはインピーダンスチャートとこれを左右裏返しにコピーしたアドミッタンスチャートの2枚で計算します。ここではインピーダンスチャートとアドミッタンスチャートで計算した例を示します。

(1)正規化インピーダンス、アドミッタンスを導出する
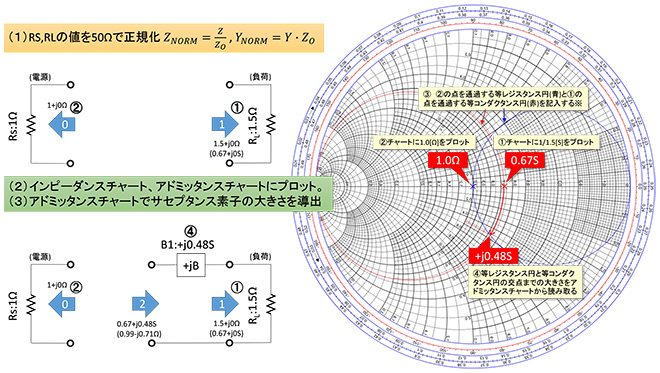
信号源と負荷のインピーダンスをスミスチャートにプロットできるようにチャートの中心のインピーダンス（Zo：ここでは従来通り50Ωとします）で正規化します。計算式は図9の（１）に記載の通りです。図9ではアドミッタンスチャートしか示していませんが、インピーダンスチャートとアドミッタンスチャートの両方にプロットしましょう。
なおMr.Smithでは正規化計算は自動で処理されるので必要ありませんでした。

(2)等レジスタンス円、等コンダクタンス円を書き込む
コンパスを使用して両チャート上に図9②の点を通る等コンダクタンス円と①の点を通る等レジスタンス円をそれぞれ書き込みます。②の点を通る等コンダクタンス円はインピーダンスチャート上でjX=0のレジスタンスメモリ上に中心があり、0Ωと1.5Ω（②の点）を結ぶ線の大きさが直径となる円、①の点を通る等レジスタンス円はインピーダンスチャート上でjX=0のレジスタンスメモリ上に中心があり、1.0Ω（①の点）と∞Ωを結ぶ線の大きさが直径となる円です。円の中心はコンパスを使用して各直径区間を２等分することで導出してください。インピーダンスチャート上での作図は図9を、アドミッタンスチャート上での作図は図10を参考にしてください。なおMr.SmithではMarker listから通過させたいマーカを選択して、カーソル（C）→Constant G（等コンダクタンス円）、カーソル（C）→Constant R（等レジスタンス円）で表示することができました。

(3)サセプタンス素子の導出
負荷インピーダンスにサセプタンス素子を接続して、等コンダクタンス円と等レジスタンス円の交点までインピーダンスを変換し、そこからリアクタンス素子を接続して負荷の共役インピーダンス（50Ω）までインピーダンスを変換します。
サセプタンス素子の大きさは図9に示す通り、等コンダクタンス円上の②から等レジスタンス円との交点④までの大きさをアドミッタンスチャートの目盛りを読み取って求めます。
Mr.Smithでは目盛りを読む代わりに、接続する「並列素子」の大きさを変化させて交点までインピーダンスを変化させました。

図9　練習問題の解法　ステップ(1)～(3)

※円の中心を求める方法（2等分する方法）は下記URLなどを参照ください
https://mathwords.net/snsakuzu

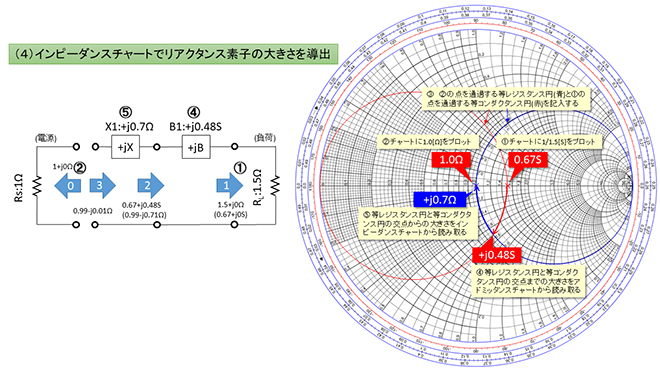
(4)リアクタンス素子の導出
リアクタンス素子の大きさはインピーダンスチャートを用いて求めます。図10に示す通り、等レジスタンス円と等コンダクタンス円の交点④から負荷の共役インピーダンス②までの大きさをインピーダンスチャートの目盛りを読み取って求めます。

Mr.Smithでは目盛りを読む代わりに、接続する「直列素子」の大きさを変化させて交点までインピーダンスを変化させました。

図10　練習問題の解法　ステップ(4)

(5)サセプタンス素子、リアクタンス素子をインダクタンス、キャパシタンスに変換
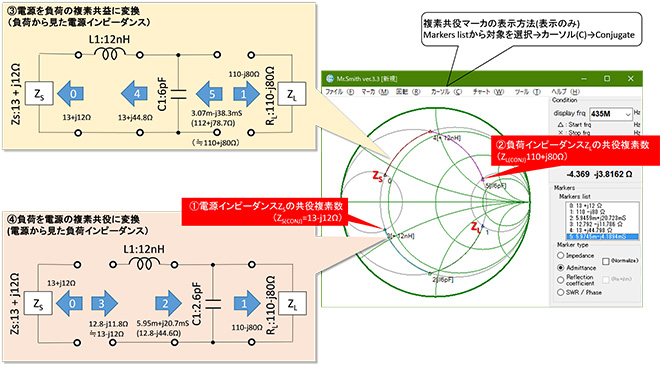
ステップ(4)まででインピーダンス変換の操作は完了しましたが、実際の回路図にするためには正規化インピーダンス／アドミッタンスを実インピーダンス／アドミタンスに変換→サセプタンスを並列リアクタンスに変換→リアクタンスを設計周波数でL,Cに変換という操作を経る必要があります。これらの操作を図11に纏めます。Mr. Smithではこれらの計算はすべて自動化していますので、リアクタンス、サセプタンスを意識せず、直接L,Cの直並列接続で整合設計を行うことができました。→図12

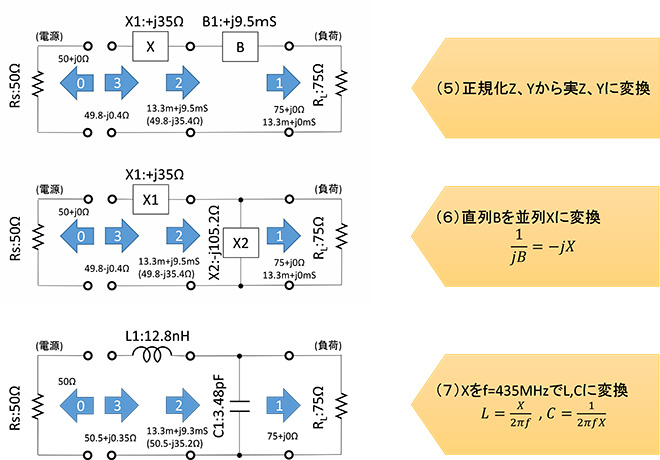
図11　練習問題の解法　ステップ(5)～(7)

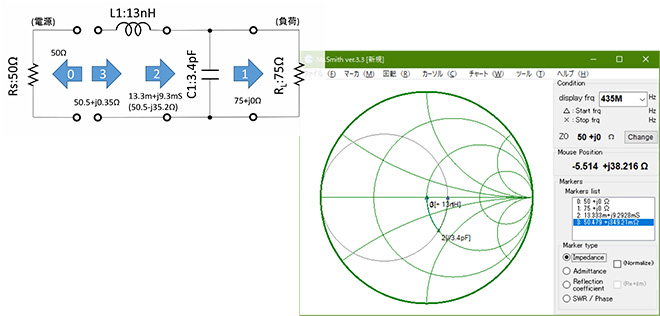
図12　 Mr. Smithを用いた整合回路設計（Step3）（第2話から再掲）

3. 改めてインピーダンスマッチングの基本

インピーダンスマッチング（整合）とは「負荷インピーダンスZLを電源インピーダンスZLの複素共益に変換する」インピーダンス変換操作です。練習問題2では簡単化のためZS、ZL共に実数値の事例で説明してきました。今度は図13に複素インピーダンス同士の整合設計例を示します。図13①、②に示すようにインピーダンスZの複素共役インピーダンスZ(CONJ)はjX=0の等リアクタンス目盛りを挟んで上下対称の点となります。Mr. Smithでは「カーソル(C)」→「Conjugate」でアクティブマーカの複素共役点を表示できます。

③に示すように、ZLをZSの複素共役インピーダンスZS(CONJ)に変換する回路は逆から辿ると、④に示すようにZSをZLの複素共役インピーダンスに変換するように働きます。従って電源側、負荷側どちらからインピーダンス変換を行っても、相手側が自身の複素共役の関係になって整合条件は満足することになります。しかし実数値どうしのインピーダンスマッチングと異なり、始点と終点のどちらを複素共役にするかを間違えると結果がでたらめになります。（例えば図13でZL(CONJ)から変換を行うと同じ定数ではZSに戻りませんので確認してみて下さい）このため初歩的な間違いを避ける観点で、インピーダンス整合は「負荷インピーダンスを電源インピーダンスの複素共役に変換する」と覚えて常に電源側、負荷側と始点、終点を意識するように心がけることをお勧めします。

図13　複素インピーダンス同士の整合設計例

4. 第3話のまとめ

第3話は本来のスミスチャートの読み方と使い方についてご説明しました。またMr. Smithとの違いについても触れました。伝送線路の話をせずに解説しているので少々モヤモヤ感が残っているかもしれませんが、少なくとも第2話の練習問題で何をやったのかはご理解いただけたのではないかと思います。要点をまとめると、
①　スミスチャートとは伝送線路の反射係数とインピーダンス値を関連付けたチャートである。
②　スミスチャートの目盛りはZoで正規化されている。
③　スミスチャートにはインピーダンスチャートとアドミッタンスチャートがあり、インピーダンスの直列接続はインピーダンスチャート、アドミッタンスの直列接続（インピーダンスの並列接続）はアドミッタンスチャートの目盛りに沿ってインピーダンス／アドミッタンスが変化する。
④　２種類のチャートは重ね合わせて使用することができる。
⑤　複素インピーダンス相互の整合回路は逆にたどると相手のインピーダンスの複素共役インピーダンスへの変換回路として機能する。
⑥　間違いを避ける観点で「負荷インピーダンスを電源インピーダンスの複素共役に変換」の手順を守る。

といった内容でした。第4話は、反射係数とスミスチャートの関係について解説するための前段階として、伝送線路と反射係数についてお話しします。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年1月号トップへ戻る

【第3話】スミスチャートとは何か（その1）

1. スミスチャートの読み方

2. 第2話の振り返り

3. 改めてインピーダンスマッチングの基本

4. 第3話のまとめ

NEWS

連載記事

テクニカルコーナー

お知らせ

外部リンク