Mr. Smithとインピーダンスマッチングの話／【第12話】λ/4線路の共振と分布定数回路(その2)｜2019年10月号

Mr. Smithとインピーダンスマッチングの話

【第12話】λ/4線路の共振と分布定数回路(その2)

濱田倫一

第11話では、λ/4線路がインピーダンス変成器として動作することを解説しました。今回はλ/4線路のもう一つの代表的な用途である「スタブ」についてご紹介します。「スタブ(stub：切り株)」とは文字通り、先端を短絡状態、または開放(切りっぱなし)にした伝送線路のことで、伝送回路や整合回路に並列に接続して、並列のLやCと同じ効果を得る分布定数回路です。

■ 1. 終端短絡線路の入力インピーダンス

第11話では負荷インピーダンスZLを長さℓの伝送線路を介して観察したときのインピーダンスZinが(式1-1)で示されることを説明しました。

$Z_{i n} = Z_{0} \frac{Z_{L} + j Z_{0} \tan β l}{Z_{0} + j Z_{L} \tan β l}$ 　　　但し $β = \frac{2π}{λ}$ （位相定数） (式1-1)

先端が短絡状態の伝送線路は「ショートスタブ」と云います。ショートスタブの入力インピーダンスは(式1-1)のZLに0Ωを代入した時の解→(式1-2)となり、Mr.Smith^※1でも計算することが可能です。

$Z_{i n} = j Z_{0} \tan β l$ 　　　但し $β = \frac{2π}{λ}$ （位相定数） (式1-2)

※1：Mr.Smithのダウンロードはこちらから

Mr.Smithでショートスタブの入力インピーダンスZinを計算する場合はZL=0Ωを「マーカ」で設定し、「回転」→「Transmission Line」メニューで線路のパラメータを指定します。図1～図3に線路の特性インピーダンスZ0を25Ω、50Ω、100Ωとしたときの終端短絡線路の線路長と入力インピーダンスの関係を計算した例を示します。

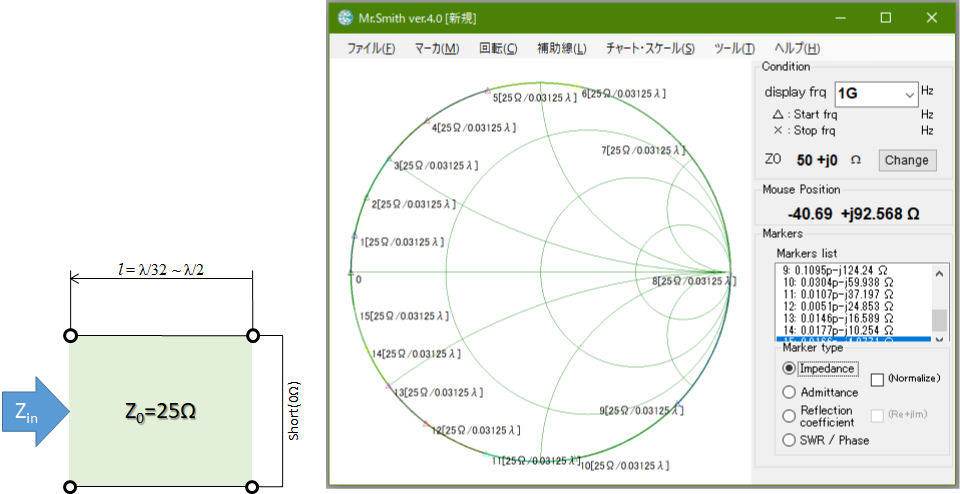
図1　先端を短絡した25Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

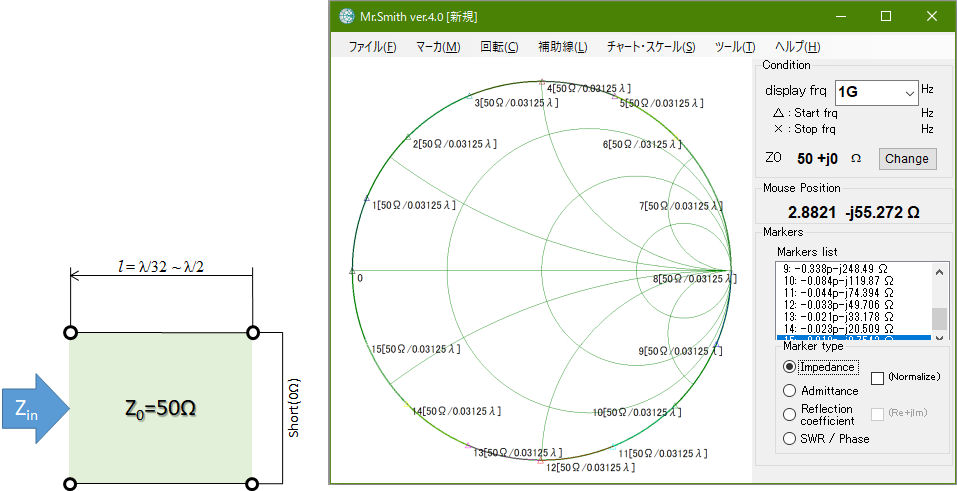
図2　先端を短絡した50Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

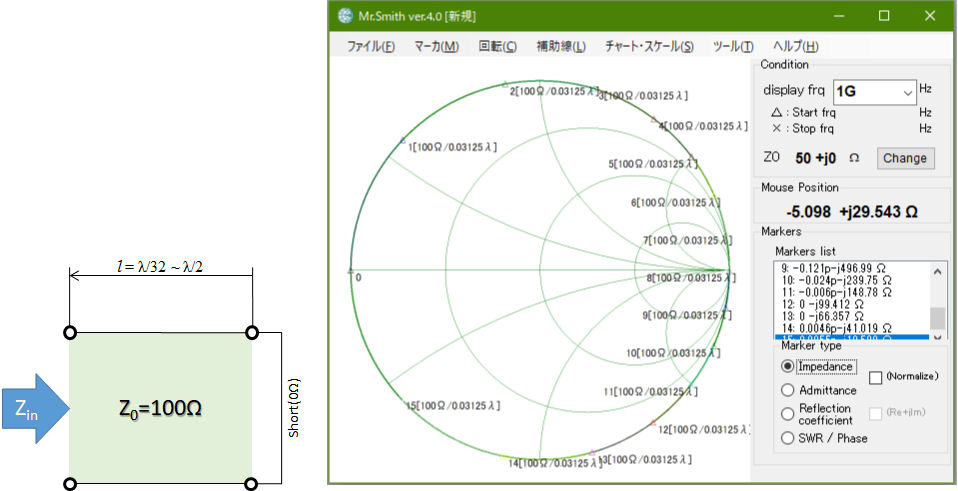
図3　先端を短絡した100Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

図1～図3でお解りいただけるように、インピーダンスローカスはスミスチャートの外周を時計回りに回転しますから、線路長がλ/4以下の長さではZinはインダクタに、線路長がλ/4の時は開放、そしてλ/4を超えてλ/2までの長さではキャパシタに見えます。この様子を図4と表1に示します。表1には1200MHz帯アマチュアバンド(1290MHz)でこのスタブを使用したときに等価的に得られるL、Cの値も示します。

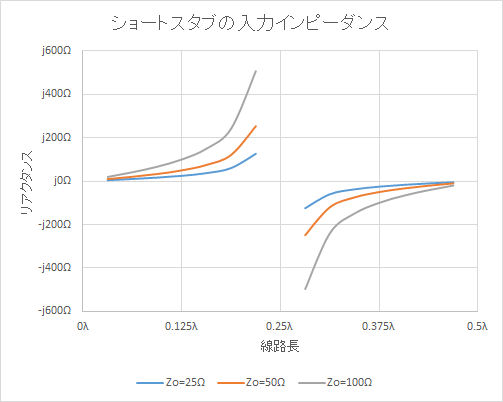
図4　先端短絡線路のZ0と線路長とZinの関係

表1　先端短絡線路のZ0と線路長とZinの関係、ならびにZinから算出した等価CまたはL

length	リアクタンス			1290MHzでの等価CまたはL
length	Zo=25Ω	Zo=50Ω	Zo=100Ω	Zo=25Ω	Zo=50Ω	Zo=100Ω
0λ	j0Ω	j0Ω	j0Ω	－	－	－
0.03125λ	j4.9792Ω	j9.9584Ω	j19.917Ω	0.61 nH	1.23 nH	2.46 nH
0.0625λ	j10.37Ω	j20.739Ω	j41.479Ω	1.28 nH	2.56 nH	5.12 nH
0.09375λ	j16.731Ω	j33.462Ω	j66.924Ω	2.07 nH	4.13 nH	8.26 nH
0.125λ	j25.049Ω	j50.098Ω	j100.2Ω	3.09 nH	6.18 nH	12.37 nH
0.15625λ	j37.515Ω	j75.029Ω	j150.06Ω	4.63 nH	9.26 nH	18.52 nH
0.1875λ	j60.608Ω	j121.22Ω	j242.43Ω	7.48 nH	14.96 nH	29.93 nH
0.21875λ	j126.82Ω	j253.64Ω	j507.29Ω	15.65 nH	31.31 nH	62.62 nH
0.25λ	－	－	－	－	－	－
0.28125λ	-j124.2Ω	-j248.5Ω	-j497Ω	0.99 pF	0.50 pF	0.25 pF
0.3125λ	-j59.94Ω	-j119.9Ω	-j239.8Ω	2.06 pF	1.03 pF	0.51 pF
0.34375λ	-j37.2Ω	-j74.39Ω	-j148.8Ω	3.32 pF	1.66 pF	0.83 pF
0.375λ	-j24.85Ω	-j49.71Ω	-j99.41Ω	4.97 pF	2.48 pF	1.24 pF
0.40625λ	-j16.59Ω	-j33.18Ω	-j66.36Ω	7.44 pF	3.72 pF	1.86 pF
0.4375λ	-j10.25Ω	-j20.51Ω	-j41.02Ω	12.04 pF	6.02 pF	3.01 pF
0.46875λ	-j4.877Ω	-j9.754Ω	-j19.51Ω	25.31 pF	12.65 pF	6.33 pF

■ 2. 終端開放線路の入力インピーダンス

先端が開放状態の伝送線路はオープンスタブと呼びます。オープンスタブの入力インピーダンスは、(式1-1)のZLに∞Ωを代入した時の解となります→(式2-1)。

$Z_{i n} = - j Z_{0} \cot β l$ 　　　但し $β = \frac{2π}{λ}$ （位相定数） (式2-1)

但し、∞Ωの代入計算は少々難解なので、Mr.Smithで計算した図5～図7のインピーダンスローカスから感覚的に理解いただくのが判りやすいと思います。ショートスタブの計算では最初にZL=0Ωをマーカで設定しましたが、今度はZL=∞Ωです。∞Ωを「R+jX」メニューで直接入力することはできないので、Z0に対して十分大きな値を代入するか、または「G+jB」メニューを指定して0Sと入力します。後は先端短絡の時と同様に、「回転」→「Transmission Line」メニューで線路のパラメータを指定します。図5~図7に線路の特性インピーダンスZ0を25Ω、50Ω、100Ωとしたときの終端短絡線路の線路長と入力インピーダンスの関係を計算した例を示します。

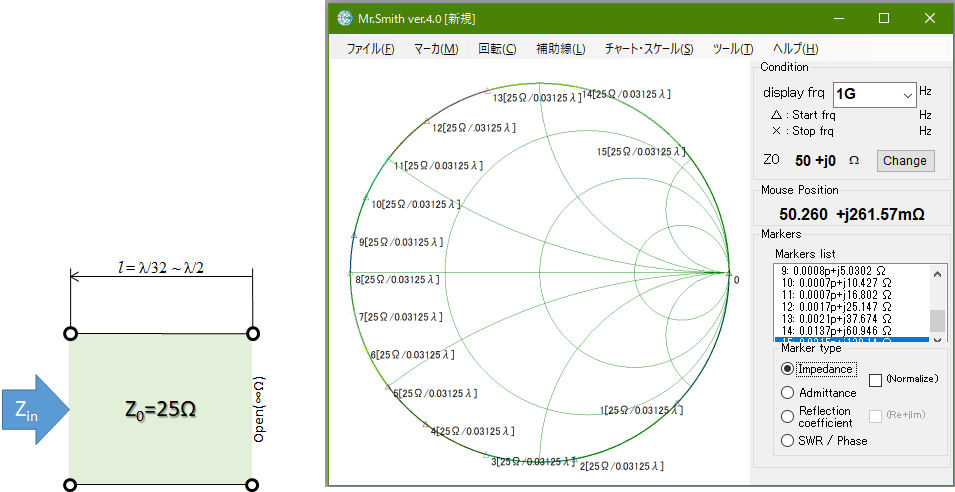
図5　先端を開放した25Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

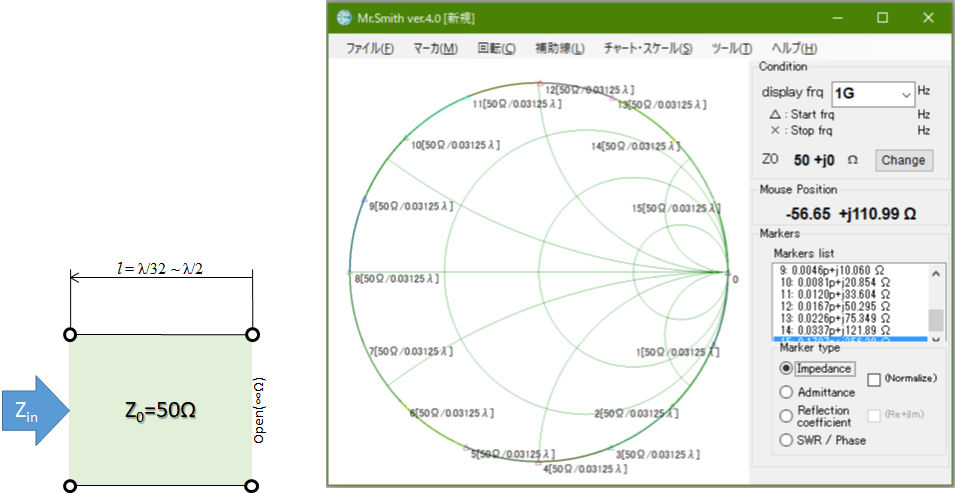
図6　先端を開放した50Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

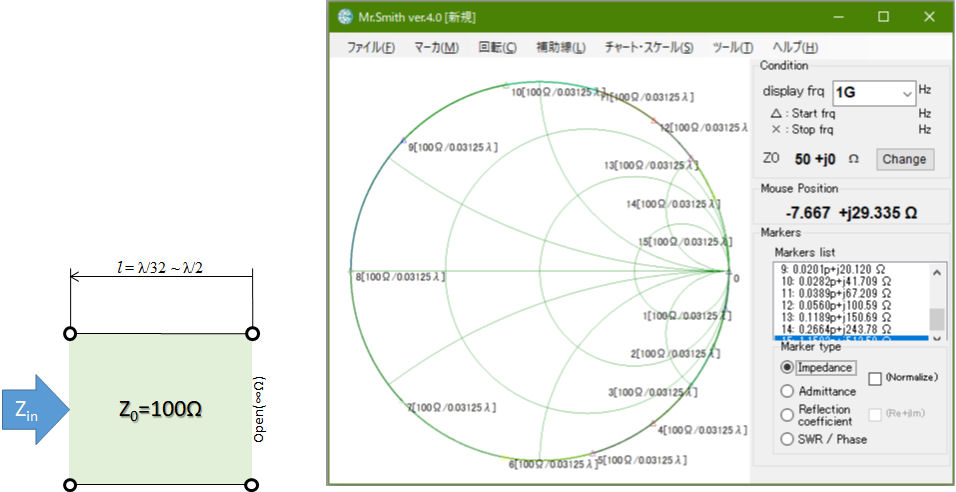
図7　先端を開放した100Ω伝送線路の入力インピーダンスをλ/16刻みで計算した例

図5～図7でお解りいただけるように、オープンスタブもインピーダンスローカスはスミスチャートの外周を時計回りに回転し、スタート点が0Ω点から∞Ω点に変わるので、線路長がλ/4以下の長さではZinはキャパシタに、線路長がλ/4の時はショート、そしてλ/4を超えてλ/2までの長さではインダクタに見えます。この様子を図8と表2に示します。表2には1200MHz帯アマチュアバンド(1290MHz)でこのスタブを使用したときに等価的に得られるL、Cの値も示します。

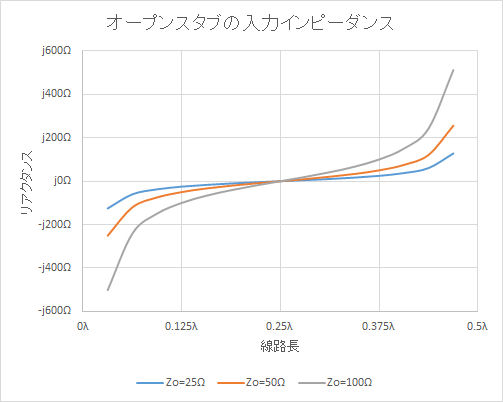
図8　先端開放線路のZ0と線路長とZinの関係

表2　先端開放線路のZ0と線路長とZinの関係、ならびにZinから算出した等価CまたはL

length	リアクタンス			1290MHzでの等価CまたはL
length	Zo=25Ω	Zo=50Ω	Zo=100Ω	Zo=25Ω	Zo=50Ω	Zo=100Ω
0.03125λ	-j125.5Ω	-j251Ω	-j502.1Ω	0.98 pF	0.49 pF	0.25 pF
0.0625λ	-j60.27Ω	-j120.5Ω	-j241.1Ω	2.05 pF	1.02 pF	0.51 pF
0.09375λ	-j37.36Ω	-j74.71Ω	-j149.4Ω	3.30 pF	1.65 pF	0.83 pF
0.125λ	-j24.95Ω	-j49.9Ω	-j99.8Ω	4.95 pF	2.47 pF	1.24 pF
0.15625λ	-j16.66Ω	-j33.32Ω	-j66.64Ω	7.41 pF	3.70 pF	1.85 pF
0.1875λ	-j10.31Ω	-j20.62Ω	-j41.25Ω	11.97 pF	5.99 pF	2.99 pF
0.21875λ	-j4.928Ω	-j9.856Ω	-j19.71Ω	25.05 pF	12.52 pF	6.26 pF
0.25λ	0Ω	0Ω	0Ω	－	－	－
0.28125λ	j5.0302Ω	j10.06Ω	j20.121Ω	0.62 nH	1.24 nH	2.48 nH
0.3125λ	j10.427Ω	j20.855Ω	j41.709Ω	1.29 nH	2.57 nH	5.15 nH
0.34375λ	j16.802Ω	j33.605Ω	j67.209Ω	2.07 nH	4.15 nH	8.30 nH
0.375λ	j25.148Ω	j50.295Ω	j100.59Ω	3.10 nH	6.21 nH	12.42 nH
0.40625λ	j37.675Ω	j75.35Ω	j150.7Ω	4.65 nH	9.30 nH	18.60 nH
0.4375λ	j60.947Ω	j121.89Ω	j243.79Ω	7.52 nH	15.05 nH	30.09 nH
0.46875λ	j128.15Ω	j256.29Ω	j512.59Ω	15.82 nH	31.64 nH	63.27 nH

■ 3. 分布定数回路によるRFチョーク回路

最後にスタブ回路の使用例をご紹介します。図9に示す回路はチョーク回路と呼ばれ、マイクロ波やミリ波の増幅回路においてトランジスタにDCバイアスを加える目的で頻繁に使用されます。伝送線路は第11話で紹介したマイクロストリップ線路を用い、プリント基板上に実際に図9の左側に示すようなパターンを配置して構成します。

まず幅の広い線路(Low Z0)は先端開放のスタブ線路となっていますので、動作周波数において開放端からλ/4離れたA点は、仮想短絡(GNDに短絡と同等)点となります。この点からFETのドレインに接続される細い線路(High Z0)は、動作周波数においてはA点が仮想短絡点なので、先端短絡のスタブ線路と見なすことができます。従って、この線路のドレイン端のインピーダンスは∞Ωとなり、ドレインの主信号系回路からは当該バイアス回路は見えません。等価的に幅の広い線路はバイパスキャパシタ、幅の狭い線路はチョークインダクタと同様の機能を果たしています。Cの機能を持たせる線路を低Z0とするのは、図8から判るように周波数(波長)の変動に対してA点のインピーダンスを低く保つため、同様にLの機能を持たせる線路を高Z0とするのは、図4から判るように周波数(波長)の変動に対してドレイン端のインピーダンスを高く維持するのが目的です。

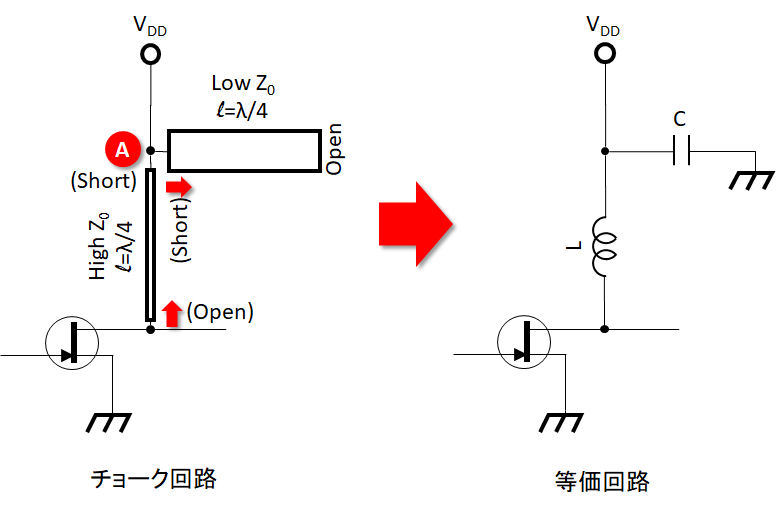
図9　分布定数回路によるチョーク回路