Mr. Smithとインピーダンスマッチングの話／【第13話】<em>Q</em>とは何か(その1)｜2019年11月号

Mr. Smithとインピーダンスマッチングの話

【第13話】Qとは何か(その1)

濱田倫一

【第13話に入る前に】お詫び、他

(1) 読者の方からご指摘があり、第11話と第12話の(式1-1)に下記の通り誤記があることが確認されました。月刊FB NEWS編集部にご対応頂き2019年10月15日以降は第11話、第12話共、修正済みです。申し訳ありませんでした。

(2)「2.終端開放線路の入力インピーダンス」の項で、上式のZLに∞Ωを代入して解くのは少々難解と書きましたが、同じ読者の方から「それほど難しくないので解説すべき」と、解法を添えてご意見を頂きました。(式1-1)から(式2-1)は以下の通り導出されます。

ご指摘ありがとうございました。

第11話～第12話で、分布定数回路の基本的な考え方と設計方法についてご紹介しました。第13話からは、これまでと少し毛色の違うお話です。電子工学でQという諸元は比較的マイナーで、電子部品の善し悪しを表現するパラメータと捉えられがちです。筆者は”Q”という文字を見ると、円谷プロダクションの特撮TVドラマ「ウルトラQ」を連想してしまいます(歳がばれてしまいますね…古い話で恐縮です。) 第13話～第14話ではこの怪しげな諸元「Q」の意味するところを解説します。

1. 久々にインピーダンスマッチングのお復習い

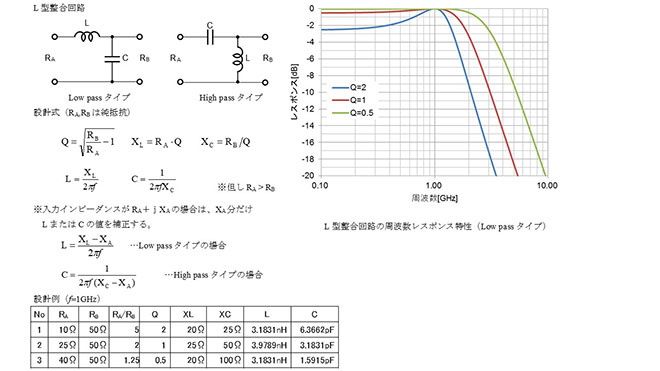
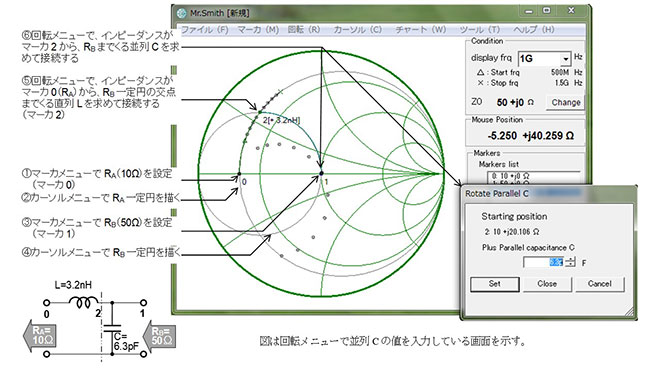
第2話で説明しましたが、インピーダンス変換の基本回路は図1に示すような、直並列のリアクタンス素子の組み合わせ回路です。素子の並び方から、L型回路、Lマッチ回路などと呼ばれます。この回路はスミスチャートを用いて設計すれば、その動作が視覚的によく理解できると思います。Mr. Smith^※1を使用すれば図2に示すように簡単に設計できます。

※1　Mr. Smithのダウンロードはこちらから。

図1　L型整合回路の設計式と設計例

図2　Mr. Smithで整合回路を設計する方法

スミスチャートを使用せずにL,Cの値を求めるには図1の計算式を用い、入出力のインピーダンス比(RB/RA)からQを算出し、この値からXL,XCを導出した上で、設計周波数を用いてL,Cの値に変換します。

このQの値が大きくなるほど、レスポンス特性は狭帯域になります。この計算式は入出力とも純抵抗(…jX成分が存在しない)であることが条件になりますので、入力にjX成分が存在する場合は、これを相殺する-jX成分を直列接続してjX=0[Ω]にした上で、図中の計算式を適用します。ところで、ここで登場する「Q」とは一体何でしょうか。

2. Q(Quality factor)とは何か？

QとはQuality factorの頭文字をとったもので、共振回路の尖鋭度を示す値として教科書に登場し、共振周波数fOにおけるQは、図3、図4に示すとおり、共振周波数におけるリアクタンス(以下X)とレジスタンス(以下R)の比(|X|/R)、またはコンダクタンス(以下G)とサセプタンス(以下B)の比(G/|B|)で定義されると記載されています。回路設計においては、この概念を拡張し、回路または部品のXとRの比として、以下に述べる3種類のQを取り扱います。

(1) L,CのQ(損失係数の逆数としてのQ)
理想的なインダクタ(L)やキャパシタ(C)は、端子電圧と電流に90°の位相差が生じますが、実際のLやCでは、漏れ磁束や誘電体損による損失が生じるため、図3に示すように、位相差が90°以下の値になります。

この電圧と電流の位相差の減少分を示すのがtanδ(誘電正接)、その逆数が部品の単体Qとなります。tanδは0のとき無損失で値が大きくなるほど損失が大きくなり、Qは値が大きくなるほど損失が小さく、無損失の時はQ=∞になります。またQもtanδもリアクタンス(X)とレジスタンス(R)の比になるため、周波数の関数となり、周波数が高くなるほどQは高い値、tanδは小さい値を示します。

図3　インダクタとキャパシタのQ

並列素子として表現される損失を示すときはtanδ、直列損失を示すときはQを使用するケースが多く、「誘電正接」の名の通り、Cの損失を表示するときはtanδを、Lの損失を表示するときはQを多く使用します。

(2)共振回路のQ
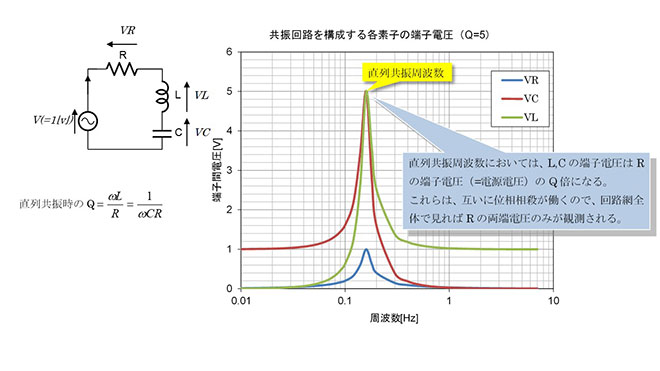
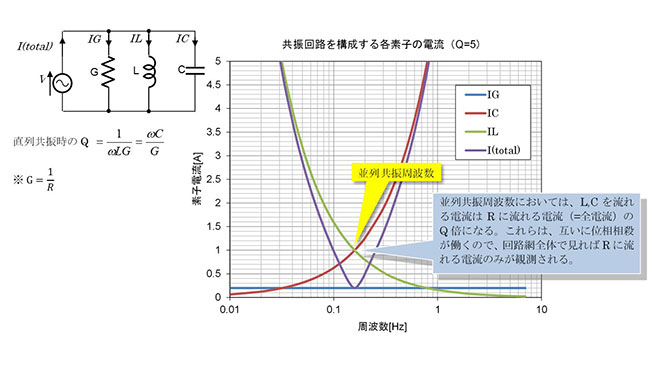
一般に教科書に登場するQの事で、図4、図5に示すとおり、共振回路の共振周波数におけるXとRの比を示します。物理的には、この値は共振回路の損失を示しており、共振時のL,C端子電圧(または電流)が、電源電圧(または電流)の何倍になるかを示す値です。

つまり共振回路が共振すると、LやCには直列共振の場合は印加電圧のQ倍大きな電圧、並列共振の場合は流入電流のQ倍大きな電流が生じます。このためHPA出力などの大電力回路に適用する共振回路では素子の耐圧や耐電流が問題になります。共振回路のQはL、Cそれぞれの損失抵抗の合成値で決まりますが、実際のところ、世の中のL,Cの損失を比較すると、Lの損失の方がCより10倍以上大きいというのが実態です。これは、インダクタの実現にはコイル構造が必要で、キャパシタと比較して大型化する傾向にあり、その結果巻き線抵抗や輻射による損失が発生しやすくなる事に起因します。この結果、共振回路のQは使用しているインダクタのQとほぼ同じ値になります。このためデバイスのQと共振回路のQはあまり区別せずに使用されているのですが、混乱の元であり、厳密には別物と考えるべきです。

図4　直列共振回路のQ

図5　並列共振回路のQ

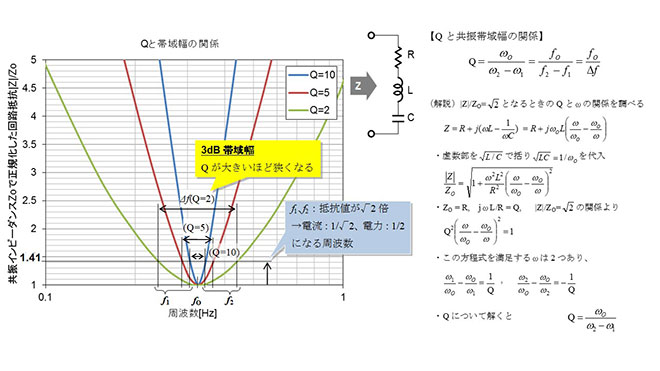
本章の冒頭で述べたとおり、共振回路におけるQは共振の尖鋭度を示します。Qと共振帯域(電力半値幅：振幅が共振周波数の-3dBとなる帯域幅)の関係は図6に示す通りで、Qが高いほど、帯域が狭くなることが判ります。

図6　帯域幅とQの関係

(3)回路設計上のQ　(動作Q)
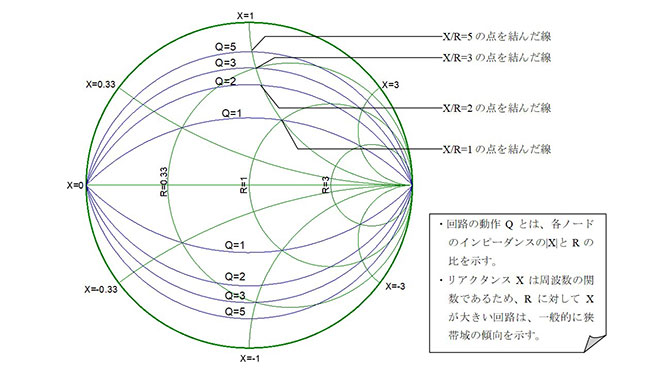
回路の動作Qと呼ばれるもので、回路の各ノードにおけるXとRの比を示します。回路インピーダンスとQの関係をスミスチャート上に表すと、図7のようになります。この「X/R=一定値」の軌跡は「定Q円」とも呼び、Mr. Smithでも、「チャート(W)」→「Q cursor」→「Draw」と選択して表示されるウィンドウから所望のQ値を入力すれば表示することが可能です。なおLCのQや、共振回路のQが、素子や回路の物理的な損失の大きさを示す値であるのに対して、回路の動作Qは単にX/Rを示す値であって、回路の損失を直接示す値ではありません。

図7　回路の動作Q

3. 回路設計上のQと帯域の関係

話を図1の計算式に登場するQに戻します。ここまでお話すれば、察しの良い方はお気づきと思いますが、図1のL型整合回路を設計するときに登場するQとは、2章で述べた3種類のQのうちの「(3)回路設計上のQ」に該当します。

図8～図10は図1の表に示した動作Q=2，1，1.5のそれぞれのインピーダンス変換回路について、Mr. Smith上でインピーダンス軌跡を計算したものです。ある抵抗値RAを別の抵抗値RBに変換するには、リアクタンス成分とサセプタンス成分を交互に付加(＝L型回路)して実抵抗目盛を移動する必要があり、必ず回路の動作Qが上昇します。図8に示した通り、図1の計算式に登場した”Q”とは、この動作Qの上昇分を示しており、L型回路のインピーダンス変換比が大きくなるほど動作Qは高くなります。図8～図10は500MHz~1.5GHzの帯域で計算を行っており、VSWR=1.5の補助スケールを表示させています。3つの図を比較すると、動作Qが低いほどVSWR<1.5の領域に入る周波数範囲が広くなる…つまり整合がとれる周波数帯域が広くなります。この事は、図1のグラフとも一致する傾向です。

図8　L型整合回路の設計例1(Q=2、10Ω→50Ωへの変換)の整合帯域^※2

図9　L型整合回路の設計例2(Q=1、25Ω→50Ωへの変換)の整合帯域^※2

図10　L型整合回路の設計例3(Q=0.5、40Ω→50Ωへの変換)の整合帯域^※2

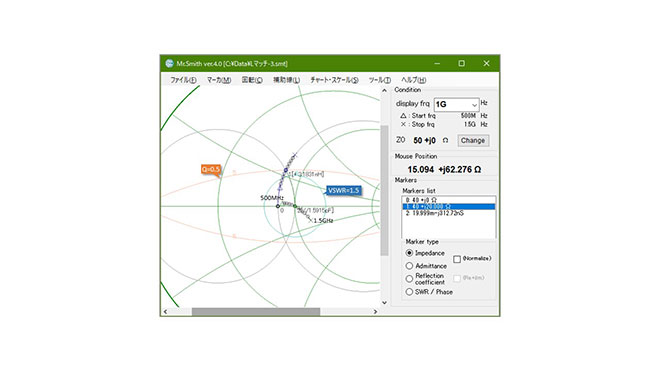
図11　L型整合回路の設計例3(Q=0.5、40Ω→50Ωへの変換)の整合帯域(拡大)^※2

※2　図8～図10は制作中のMr. Smith ver4(未公開)を使用して作成したためメニュー表記やカーソルの色設定が公開中のMr. Smith ver3.3と少し異なっています。ご了承ください。

4. 第13話のまとめ

第13話では”Q”とは何か？とインピーダンス整合回路との関係についてご説明しました。
① 　QとはリアクタンスXとレジスタンスRの比(X/R)を表す諸元で、インピーダンスと同様、デバイスのQ、共振器のQ、回路の動作Qの3つに分類できます。
② 　デバイスのQはインダクタンス(磁性体)やキャパシタンス(絶縁体)の損失を示す諸元で、tanδの逆数です。Qが大きい程損失が小さくなります。
③ 　共振器のQはタンク回路(共振器)の損失と共振帯域幅を示す諸元です。Qが大きい程、損失が小さくなり、共振帯域幅が狭く(共振が鋭く)なります。
④ 　回路の動作Qは、回路の各ノードにおけるリアクタンスXとレジスタンスRの比(X/R)を表しており、Qが大きい程回路の通過帯域幅が狭くなります。
⑤ インピーダンス整合回路においては、インピーダンス変成比が大きくなるほど、回路の動作Qが大きくなり、結果、整合できる周波数帯域が狭くなります。

それにしても”Q”…なんともミステリアスな印象を受けます。通常、物理諸元の名称は、名称と物理的意味合いが直接的にリンクしているものですが、”Q”という諸元は、物理的な意味合いが全く読み取れません。「なぜ ”Q” と呼ぶのか」(こだわっているのは筆者だけかもしれませんが)の理由を筆者は知りませんが、恐らく、インダクタが、共振回路やフィルタ回路の性能を決めてしまうケースが多い事から、コイルの「品質」を表すパラメータとして用いられた経緯があり、「Quality Factor」の頭文字をとって「Q」と呼ばれるようになったのだと思っています。何方かご存じの方がおられましたらご教示頂けないでしょうか。

次回はデバイスのQと回路の動作Qの関係や、Qを意識したインピーダンス整合回路の設計方法について解説します。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年11月号トップへ戻る

【第13話】Qとは何か(その1)

1. 久々にインピーダンスマッチングのお復習い

2. Q(Quality factor)とは何か？

3. 回路設計上のQと帯域の関係

4. 第13話のまとめ

NEWS

連載記事

テクニカルコーナー

お知らせ

外部リンク