Mr. Smithとインピーダンスマッチングの話／【第15話】<em>Q</em>とは何か(その3)｜2020年1月号

Mr. Smithとインピーダンスマッチングの話

【第15話】Qとは何か(その3)

濱田倫一

第14話は図らずも市販デバイスのデータシートにスペックとして記載されているQ値とSパラメータが如何に一致しないか･･･というテーマになっていまいました。筆者も少し力尽きてしまって雑な結論を書いてしまいましたが、このように測定誤差の影響を受けやすい諸元なので、
　①デバイス選定に際してはできるだけ大きな値を確保すべき
　②回路シミュレーションに用いる損失抵抗を導出する際は、Q値からではなく、Sパラメータを用いるべき
というのが第14話の結論です。ではQが小さいデバイスを使用すると何が起きるのか。

第15話ではスペックとして定義されたQ値から離れ、Sパラメータ(等価回路)から導出したQ値を用いて、デバイスQと共振器のQ、回路の動作Qの関係をご説明します。

1. デバイスのQと共振回路のQの関係

電子工学や無線工学の教科書では、主に共振回路のQに力点をおいた解説がなされており、デバイスのQと共振回路のQの関係はあまり触れられていないと言うのが一般的です。実際の設計現場では共振回路を構成するL、Cは別々のデバイスであり、それぞれに損失があってQの値も区々です。ここでは第14話で使用した太陽誘電製のキャパシタEVK105CH020BW-F(2pF)とCoilCraft製のインダクタ0908SQ8N1(8.1nH)を用いて共振回路を組んだときの特性を調べて見る事にします。2pFと8.1nHで共振回路を構成したときの共振周波数foは（式1-1）から1.25GHzとなります。

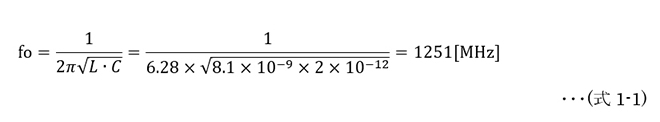
(1) Sパラメータから導出したキャパシタの等価直列抵抗とQ
メーカが提供するS2PファイルからEVK105CH020BW-F(2pF)の等価直列抵抗を導出する作業は第14話で行い、図4に結果を示しました。

同図より、このキャパシタの等価直列抵抗は0.2Ω、1.25GHzでのQは(式1-2)から318となります。

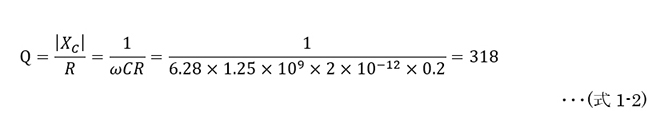
(2) Sパラメータから導出したインダクタの等価直列抵抗とQ
キャパシタと同様、0908SQ8N1（8.1nH）の等価直列抵抗は、第14話の図7から0.24Ω 、1.25GHzでのQは（式1-3）から265となります。

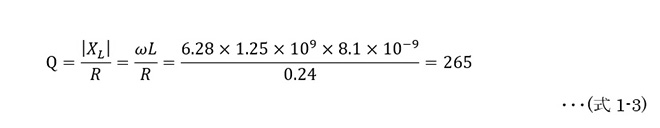
(3) 直列共振回路を構成したときのQ
次にこれらのLCを組み合わせて共振回路を構成したときのQを計算してみます。

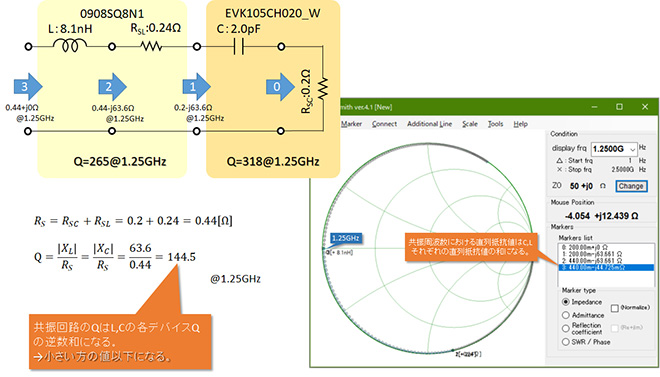
まず直感的にわかりやすい直列共振回路から･･･。直列共振周波数における等価直列抵抗RはMr.Smith^※1を用い、L,Cそれぞれの直列等価回路を直列に接続し、(式1-1)で求めた共振周波数(1.25GHz)でのR成分を導出します。XL、XCの値も個別にMr.Smith^※1で計算可能ですが、こちらは電卓を叩くほうが早いと思います。図1に結果を示します。1.25GHzは共振周波数なので|XL|=|XC|=63.6Ω、R=0.44Ωで、共振Q=144.5となりました。実は図1をよく見ると|XC|はMr.SmithでRを計算する過程で導出できています。(マーカ1のX成分)

図1　直列共振回路のQを導出する

※1　Mr.Smithのダウンロードはこちらから

図1の回路に示す通り、直列共振回路においては各デバイスの等価直列抵抗が直列に合成されるのに対して、|X|の値はL,Cいずれかの値(どちらも同じ大きさ)なので、共振Qの値は各デバイスQの値より小さくなり、各デバイスQの逆数和(の逆数)となります。→(式1-4)

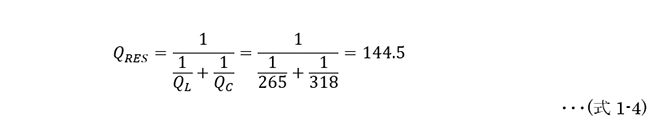
(4) 並列共振回路を構成したときのQ
では並列共振回路を構成したときはどうなるでしょうか。導出の手順は直列共振回路の時と基本的に同じですが、直列接続された素子を並列接続するので、作業は少々面倒です。またMr.Smith ver.3.3では直列接続回路の並列接続計算で周波数スイープを行うことができません。ここでは1.25GHz一点での計算結果を示します。

手順①：各デバイスの1.25GHzでのインピーダンスを計算する
図2に示す通り、各デバイスの直列等価回路の1.25GHzにおけるインピーダンスを個別に導出してメモに控えます。

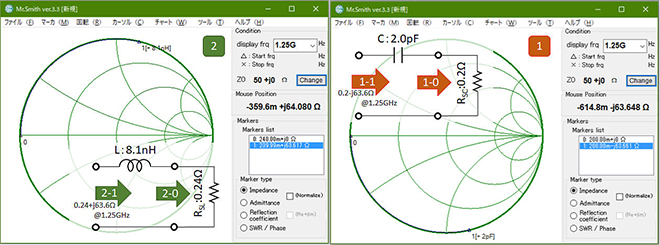
図2　各デバイスの1.25GHzにおけるインピーダンスの導出

手順②：求めたインピーダンスを並列接続する
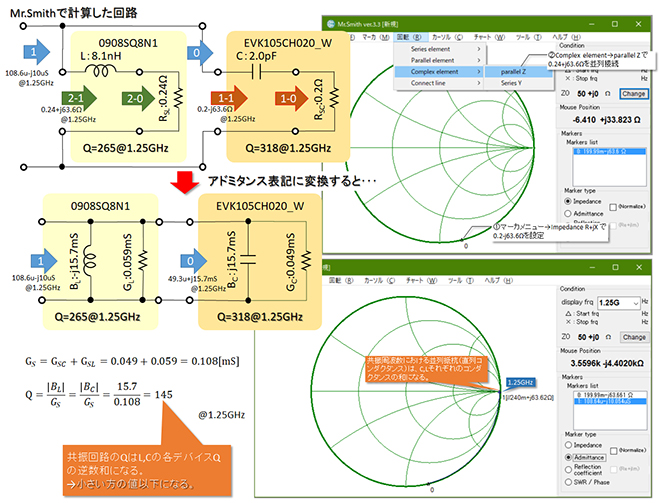
図2で求めたインピーダンスを以下の手順で並列接続します。(図3の右上を参照)
「ファイル」→「新規」で過去の計算をクリア
「マーカ」→「Impedance R+jX」でキャパシタのインピーダンス(0.2-j63.6Ω)を入力
「回転」→「Complex element」→「parallel Z」でインダクタのインピーダンス(0.24+j63.6Ω)を入力
これで各デバイスのインピーダンスが並列接続され、Markers listの中に、1:108.64u-10.054uSという計算結果が表示されます。

図3　各デバイスのインピーダンスを並列接続する

手順③：計算結果からQを導出する
並列共振の場合、リアクタンスが無限大になるため、直列抵抗Rの値は直接観測できず周波数の関数になってしまいます。(第14話の3. (2)参照)

並列共振回路のQを求めるには損失抵抗(等価直列抵抗)RSに替えて損失コンダクタンスGSを用います。Mr.Smithでは並列接続を行って新しく生成されるマーカはデフォルトでアドミッタンス表記となるので、表示されているマーカの実数部分が損失コンダクタンスGSと言うことになります。GS=0.108mS、|XL|=|XC|=63.6Ω((3)で求めた値)より、

※Xに対してRの値が十分に小さいため簡易的に計算しています。正しくは1/(R+jX)の計算が必要です。

Bを簡易計算したので、少し計算誤差が出ましたが、直列共振のときと同じ結果が得られました。計算式からお解り頂けると思いますが、Mr.Smithで計算した図3左上の回路は、その下に記載した、アドミタンスの従属接続回路に置き換える事ができます。この置き換えた回路上では、直列共振と同様、共振回路の損失コンダクタンスGSは、各デバイスの損失コンダクタンスGL､GRの和となります。共振Qの値がデバイスQの逆数和になるのも直列共振と同じです。

(5) 共振回路に必要なデバイスQ
第13話の図6に示したように、共振回路のQは共振の帯域幅を決定します。従ってIFトランスやコレクタのタンク回路等、所望の帯域のみを通過させたり増幅させたりするための共振回路では、帯域幅で共振回路に必要なQが決定されます。従って、このような共振回路に適用するLやCのデバイスQは逆数和が共振回路の要求するQよりも小さくならないように選定する必要があります。

2.デバイスのQと回路の動作Qの関係

次にデバイスQと回路の動作Qの関係を調べてみましょう。ここでは第13話の1.で解説した Lマッチ回路の設計に登場する動作Qと回路を構成するデバイスのQとの関係を説明します。

図4に示す、5Ω→50Ωのインピーダンス変換回路を考えてみます。周波数は引き続き1.25GHzとします。またここでは市販のデバイスではなく、理想諸元を用いて設計しています。この回路の動作Qは第13話の図1に示す式から、

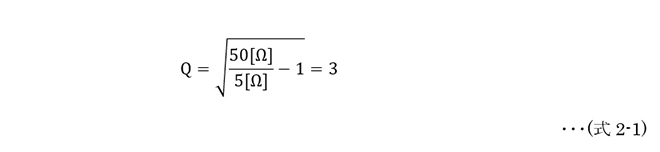
となります。このことは図4のスミスチャートに表示されている定Qスケールからも読み取れます。

図4　5Ωから50Ωへの変換回路　

では、このインピーダンス変換回路に使用しているインダクタ(1.9nH)のデバイスQを有限の値にしてみるとどうなるか調べてみましょう。インダクタのデバイスQが動作Qの10倍の30の場合と、その半分の15のケースをシミュレーションしてみます。

まず等価直列抵抗RSを求めます。

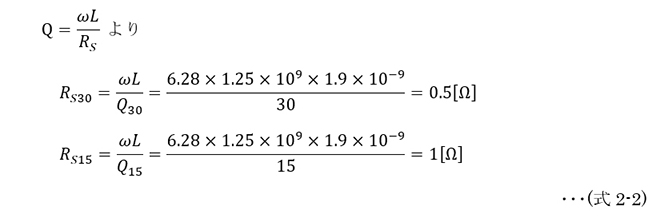
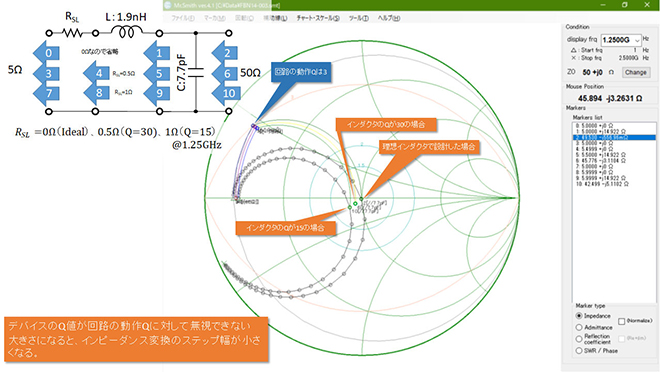
図5に(式2-2)で導出したRSを図4のL(1.9nH)に直列に接続して計算した結果を示します。

図5　デバイスQの影響

図5に示すようにインダクタのQが低下すると理想諸元での設計結果に対して、インピーダンス変換のステップ幅が小さくなり、またX=0Ωとなる周波数が低くなります。理想設計から乖離する大きさはデバイスQが小さくなるほど大きくなるのですが、計算結果からお解りいただけるように、デバイスQが動作Qの10倍あっても理想設計からは乖離しています。Mr.Smithを使って計算して頂くと判りますが、この回路の場合、理想諸元の設計結果を正確に再現させようとすると、インダクタのデバイスQは150以上必要で、回路の動作Qの50倍と云うことになります。一般論として理想諸元で整合回路やフィルタ回路を設計通りに動作させようとすると、動作Qの100倍程度のデバイスQが必要になります。動作Qの高い回路は設計通りに作動しないケースが多いのは、このような理由にあります。

3. 第15話のまとめ

第15話ではデバイスQと共振器のQ、回路の動作Qの関係をご説明しました。
要約すると、
①共振回路のQは回路を構成するL、CそれぞれのデバイスQの逆数和(正確には逆数和の逆数)になる。
②共振回路に使用するデバイスのQは、この逆数和の逆数が共振器に要求されるQ(帯域幅で決まる)よりも大きい必要がある。
③デバイスQと共振回路のQの関係は、直列共振でも並列共振でも同じである。
④回路を計算通りに動作させる為には、回路を構成するデバイスのQは、動作Qの50～100倍程度の値が必要になる。

といった内容でした。共振回路におけるQは共振帯域を決めると説明しましたが、共振回路をフィルタとして使用する場合、共振回路のQはできるだけ高くして、帯域特性は共振回路と入出力回路の結合度で調整するのが一般的な設計です。また本稿では触れませんでしたが、共振回路をタンク回路として捉えた場合、QはデバイスのQと同様に損失係数となります。発振回路などに適用する共振器ではQが低いと位相雑音性能が劣化します。回路の動作Qについては、動作Qが高くなればなるほど、回路が狭帯域になる傾向を示すと同時に、回路を構成するL、Cに高いQ値を要求することになります。言い換えると、動作Qが高い回路は部品や周囲の影響を受けやすく、再現性が悪いといえます。いたずらに動作Qの高い回路は設計しない方が再現性の観点では有利といえるでしょう。

第13話からずっと「謎の諸元」「怪しい諸元」といいましたが、Qは高周波回路の再現性を担保する上で無視できない諸元の一つです。判りにくいですが無視しないで向き合いましょう。

次回は増幅回路のお話を予定しています。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2020年1月号トップへ戻る

【第15話】Qとは何か(その3)

1. デバイスのQと共振回路のQの関係

2.デバイスのQと回路の動作Qの関係

3. 第15話のまとめ

NEWS

連載記事

JAIAコーナー

お知らせ

外部リンク