Mr. Smithとインピーダンスマッチングの話／【第25話】　そのインピーダンス、本当に存在しますか? (その2)｜2020年11月号

Mr. Smithとインピーダンスマッチングの話

【第25話】　そのインピーダンス、本当に存在しますか? (その2)

濱田倫一

第24話では、トランジスタの入出力整合回路は、必ずしもインピーダンス整合を行っていない(トランジスタが要求するインピーダンスに電源インピーダンス、または負荷インピーダンスをZ₀と仮定して変換している)ケースがあり、このような増幅器を多段接続したり、このような増幅器の前後にフィルタなど影像インピーダンスが規定されたデバイスを接続すると、段間のインピーダンスが定まらずに、設計通りに動作しなくなる可能性があることをお話しました。第25話では引き続き「インピーダンスを定める」とはどういうことかについて解説します。

1. 段間のインピーダンスを定めるとは

図1は第24話の図4の再掲です。この図においてトランジスタの出力(コレクタ)には、トランジスタの出力インピーダンスとは関係なく、ZLSという負荷インピーダンスを装荷する設計になっていて、出力にはZL→ZLSインピーダンス変換回路が挿入されています。この回路が設計通りに動作するためには、このインピーダンス変換回路に接続されているBPFのインピーダンスがZLに見えている事が必要なのですが、このBPFは影像インピーダンスがZLなのであって、実際に端子のインピーダンスがZLに見えるかどうかは反対側の端子のインピーダンス次第となります。またBPFから見たトランジスタ側のインピーダンスもBPFが要求する影像インピーダンスの値にはなっていませんので、BPFが所定の特性を発揮できない可能性もあります。

このように後段のインピーダンスが「ある値」であることを期待する回路を縦続接続すると、遠いところの負荷抵抗が回路のインピーダンスを定める役割を担うことになって、設計通りの性能が得られない原因になる場合があります。

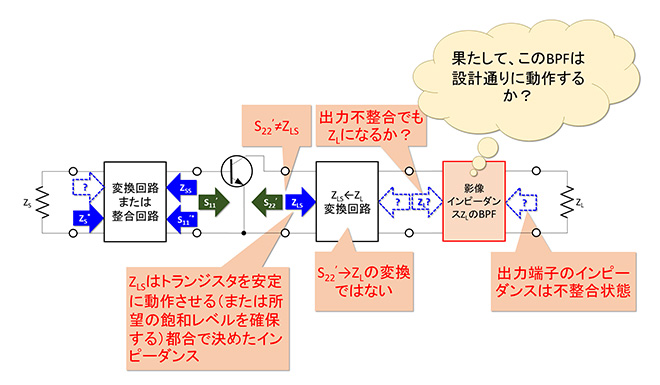
図1　遠いところにある負荷抵抗(第24話から再掲)

理論的には遠いところの負荷抵抗ZLから直後に接続された回路まで、影像インピーダンスの関係に矛盾がなければ問題なく後段回路はZLに見えるのですが、インピーダンスZ＝反射係数Γなので、遠ざかれば遠ざかるほど位相回転の影響を受けやすく、また誤差も積み上がりやすい為、負荷抵抗から離れた回路ほど設計通りに動作しなくなります。回路を安定に動作させるには、遠い後段の回路からの反射波の影響を受けないように「アイソレート」することで「段間のインピーダンスを定める」必要があるのです。(つまり、段間を「アイソレート」することと「段間のインピーダンスを定める」事は同義となります)

「後段からの反射波の影響をなくす」というのは第18話で解説したS12をキャンセルするという事に他なりません。理想的な手法は単方向化された緩衝増幅器、または単方向化されたパッシブデバイスを段間に挿入することです。単方向化された代表的なパッシブデバイスが第24話で述べたアイソレータになります。準マイクロ波帯以上の周波数帯の無線機器ではトランジスタのS12をキャンセルする事が困難な為、常套手段としてアイソレータが多用されますが、VHF以下の周波数では逆にアイソレータは大きくなりすぎて高価になる為か、殆ど見かけません。イメージインピーダンスが縦続接続されたり、整合がとれない回路を挿入する場合に段間のインピーダンスを定めて不整合の影響が後段に及ばないようにアイソレートする手段として、アイソレータの挿入以外によく使用されるのがアッテネータの挿入です。

2. アッテネータとは

アッテネータについては第17話で少し触れました。日本語では「減衰器」と称し、π型、またはT型の2ポート(四端子)回路網で構成されたデバイスで、文字通り信号電力を減衰させる働きをするものです。伝送線路に挿入される前提なので、入出力のイメージインピーダンスはZ0(通常は50Ωまたは75Ω)で設計されます。不平衡型アッテネータの基本回路構成を図2に示します。

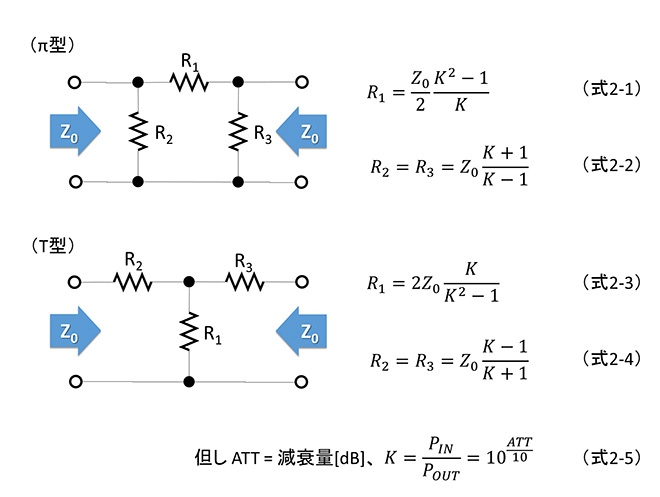
図2　アッテネータの計算式

インピーダンス変換回路と異なり、信号を減衰させるために自ら電力を消費する必要があり、回路を構成するデバイスは基本的に全て抵抗「R」です。各素子の抵抗値は、4端子パラメータと所望の入出力電圧、電流の関係を与えて連立方程式を解く事により導出できますが、結構面倒な計算になるので、一般的な回路設計では、図1に示している(式2-1)～(式2-5)を使って設計する事が殆どです。すなわち所望の電力減衰量ATT[dB]が与えられた時の真数減衰量Kは(式1-5)に示す通りとなり、Kを(式2-1)(式2-2)に適用すればπ型アッテネータ、(式2-3)(式2-4)に適用すればT型アッテネータの各抵抗値を導出することができます。第17話では計算サイトをご紹介しましたが、簡単な計算なのでExcelで計算ツールを作成したり、関数電卓にプログラムしておいて、必要なときにすぐ設計できるようにするのが良いと思います。

3. アッテネータによるアイソレーション

図3は第17話の図1の再掲です。前節で述べたとおりアッテネータは入出力のイメージインピーダンスがZ0Ωの四端子回路網なので、図3の①に示す通り、相手ポートにインピーダンスZ0Ωの信号源、または負荷抵抗が接続されていると、自ポートのインピーダンスはZ0Ωに見えます。しかし②のように相手ポートがオープンになっていると、自ポートのインピーダンスはZ0にはなりません。

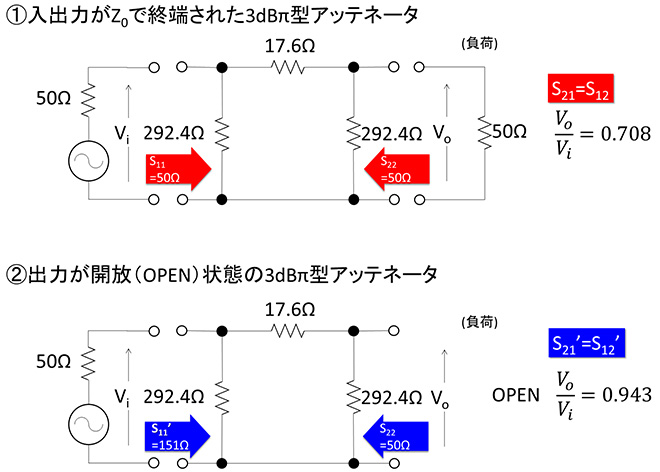
図3　Z0=50Ω3dBアッテネータの入出力インピーダンス

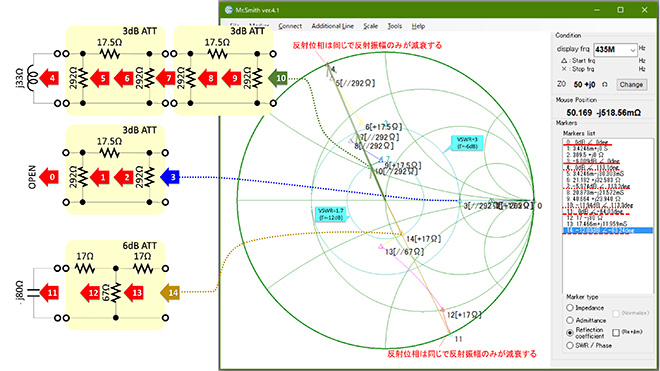
この様子をMr.Smith^※1を使って計算してみましょう。結果を図4に示します。図4の0番マーカから3番マーカまでのインピーダンスローカスが図3の②に対応した計算です。回路素子が全てRなので、始端のリアクタンス成分が0Ωだと、実抵抗目盛の上を行ったり来たりするだけの軌跡となります。図4ではMr.SmithのMarkers listのうち、アッテネータの入出力ポートに相当するものを反射係数で表示させました。0番マーカは3dBのπ型アッテネータの入力端子から、相手側を見たインピーダンスを示していますが、OPEN(何もつながっていない)なのでインピーダンスは∞Ω、反射係数Γに換算すると1∠0deg→0dB∠0degとなっています。同アッテネータの出力端子から同アッテネータ側を見たインピーダンスは3番マーカですが、0番マーカよりもチャートの内側に移動していて、Γ=-6dB∠0degとなっています。

図4　アッテネータのインピーダンス軌跡

図4では、さらにアッテネータの入力にリアクタンス成分が存在する場合も計算しています。4→7→10番マーカが、誘導性リアクタンス(ここではj33Ω)に3dBのπ型アッテネータ2段を接続したときのインピーダンスローカス、11→14番マーカが容量性リアクタンス(ここでは-j80Ω)に6dBのT型アッテネータ1段を接続したときのインピーダンスローカスを示します。

出力開放のケースでは、マーカが重なってインピーダンスローカスがよくわかりませんでしたが、リアクタンス成分が存在すると、インピーダンスローカスが等リアクタンス円、等サセプタンス円を渡りながらチャートの内側に進んで行く様子がご理解頂けるのではないかと思います。インピーダンスローカスがチャートの内側に進む＝反射係数Γが小さくなる＝インピーダンス整合状態が改善する。という事を示しています。

先程と同様に各アッテネータの入出力での反射係数Γの変化を見てみましょう。4→7→10番マーカについては、4番マーカが0dB∠113deg(0+j33Ω)、3dBアッテネータを経た7番マーカが-6dB∠113deg、さらに3dBアッテネータを経て10番マーカは-12dB∠113degとなっていて、反射波の位相一定のまま、振幅のみ減衰している事がお判り頂けると思います。同様に11→14番マーカは、11番マーカが0dB∠-64deg(0-j80Ω)、6dBアッテネータを経て14番マーカは-12dB∠-63degで、丸め誤差が出ていますが同じ傾向にあります。反射係数Γの絶対値は反射波の大きさを示しており、チャートの内側に移動するのは反射波がアッテネータで減衰するためです。

皆さんも、もうお気づきではないでしょうか、アッテネータの回路構成や入力のリアクタンス値に関係なく、アッテネータの出力の反射係数の絶対値は入力反射係数に対してアッテネータの減衰量の2乗(dBでは2倍)の大きさで小さくなっています。

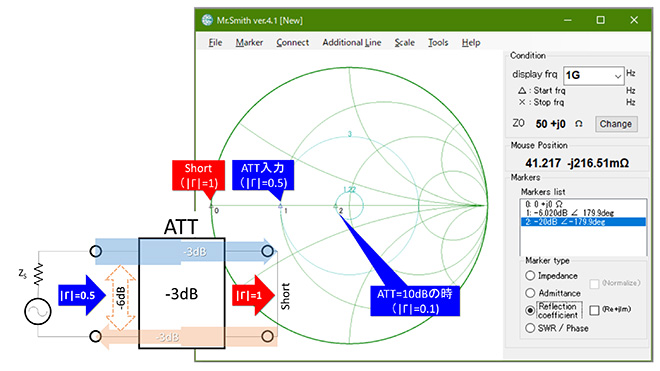
何故、反射係数はアッテネータの減衰量の2乗で小さくなるかを解説したのが図5です。

図5　反射係数が減衰量の2乗分の1になる訳

反射係数Γは入射波と反射波の比なのでアッテネータを介して反射点(ここではアッテネータの相手側端子)を観測すると、入射波が反射点に到達して観測点に戻ってくるまでに、同じアッテネータを2度通過する･･･というのがその理由です。この結果、反射点を直接観測したときと比べて、反射係数Γはアッテネータの減衰量の2乗(dBなら2倍)小さくなる、すなわちアッテネータの入出力端子はその減衰量分だけアイソレートされることになり、不整合状態が緩和されるという仕組みです。

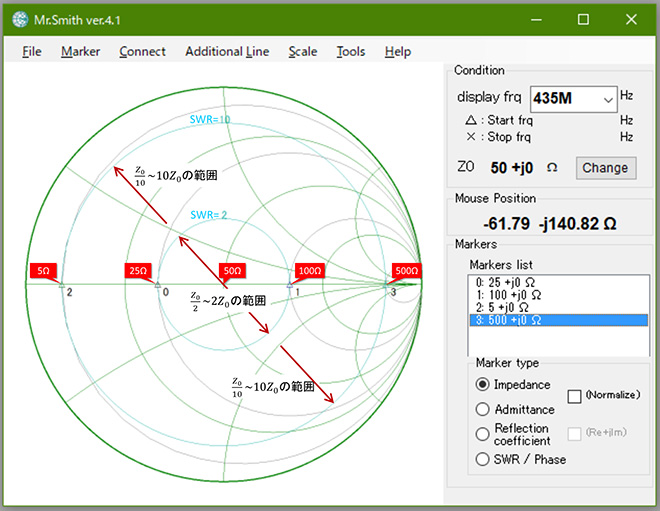
ちなみに、「反射係数を小さくする」行為は、「負荷抵抗をZ0±××Ωにする」というイメージがありますが、実際には図6に示すように負荷抵抗RLを

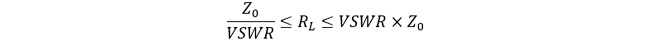
(式3-1)

の範囲に変換する行為となります。不整合状態の回路にアッテネータを挿入しても、思ったほど抵抗値がZ0に近づかない場合があります。

図6　VSWRとRLの関係

4. その他の手段

以上解説の通り、損失性のあるデバイス(つまりR)を挿入すると、反射波が減衰するため、後段の回路の影響は緩和されます。第2話以降ここまで「インピーダンスマッチング回路は電力を消費してはいけない」と説明してきましたが、今回のようにインピーダンスの定まらない回路が多段接続される場合は、インピーダンスマッチング回路に敢えてRを挿入して電力を消費させる事で、後段回路の影響を緩和する場合があります。古い設計事例で恐縮ですが、筆者が現役時代にバイブルとして愛読させて頂いた、宮本幸彦氏著　高周波回路の設計と実装(日本放送出版協会 ISBN4-14-072027-1 C2355)のP96から入力整合回路に直列抵抗を挿入した事例を図7にご紹介します。本書には整合回路に敢えてRを挿入した経緯についてのコメントはありませんが、入力側で消費電力も小さいので、安定化を期待してRを挿入されたものと理解しています。

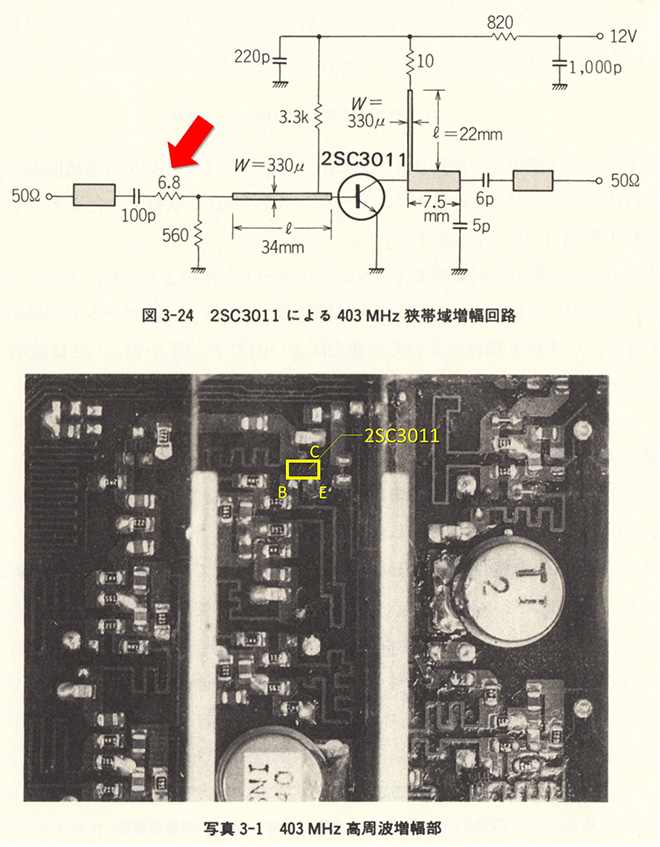
図7　Rを含む整合回路の設計事例^※2

また、ディジタル回路の出力端子や分岐配線に直列に挿入される10～30Ω程度のダンピング抵抗も反射波を減衰させる目的で挿入されるもので、同じ考え方に基づくものです。

5. 第25話のまとめ

第25話ではアッテネータを挿入することで回路の段間のアイソレーションが改善する事を解説しました。アッテネータにせよアイソレータにせよ入出力インピーダンスの定義があり、通常はZ0(50)Ωとなっています。このため、1章で登場した段間のインピーダンスZLは、アッテネータやアイソレータを挿入する場合、ZL=Z0として設計する必要があります。高周波回路では段間インピーダンス(各回路の入出力インピーダンス)を50Ωで設計することが多いですが、このような事も理由の一つです。

第1話で我々が設計上取り扱うインピーダンスには以下3種類が存在し、それぞれに対してインピーダンスマッチングが必要になる理由を説明しました。

① 負荷として電力を消費するインピーダンス…リアルなインピーダンス
② アッテネータやフィルタ等の設計上の負荷インピーダンス…イメージインピーダンス
③ 伝送線路上を電磁波が伝搬するときに定義されるインピーダンス…特性インピーダンス

これら3つのインピーダンスを「実態のあるインピーダンス」か、または「実態のないインピーダンス」か、という視点で整理すると表1のようになります。

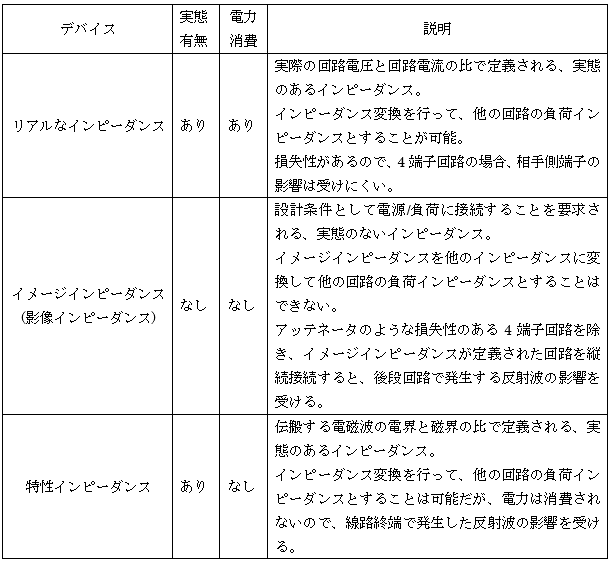
表1　インピーダンスマッチングの対象となるインピーダンス

自己の出力インピーダンスとは別の値の負荷を出力に装荷したトランジスタ増幅器の公称出力インピーダンスは厳密にはイメージインピーダンスではありませんが、便宜上イメージインピーダンスに含めています。よく「測定器では所望の性能が得られるのに、装置に組み込むとうまく性能が出ない」という経験をしますが、実態のないインピーダンスどうしの縦続接続になっている事が多く見受けられます。第25話までで一般的な増幅回路の入出力整合設計について一通りお話しました。次回からは低雑音増幅回路のお話になります。

※1　※1　Mr.Smith ver4.1のダウンロードはこちらから
https://www.vector.co.jp/soft/winnt/business/se521255.html
※2　宮本幸彦氏著　高周波回路の設計と実装（日本放送出版協会 ISBN4-14-072027-1 C2355）のP96から引用

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2020年11月号トップへ戻る