Mr. Smithとインピーダンスマッチングの話／【第17話】増幅器とSパラメータ（その2）｜2020年3月号

Mr. Smithとインピーダンスマッチングの話

【第17話】増幅器とSパラメータ（その2）

濱田倫一

第16話ではトランジスタ増幅器の入出力整合回路の基本的な考え方をご説明しました。そしてそれと同時に基本的な考え方だけでは精度の良い設計はできない現実にも触れました。

トランジスタのS11は入力インピーダンス、S22は出力インピーダンスだと言っておきながら、図7、図8で反対側ポートが50Ωでなくなると値が変わります。と申し上げたのですから、モヤモヤされていることと思います。第17話では何故トランジスタの入出力インピーダンスが反対ポートのインピーダンスの影響を受けるのかを中心に解説します。

1. そもそもの話

実は、この問題は冷静に考えると当たり前の話です。3dBのπ型アッテネータで考えてみましょう。図1の①はアッテネータの入出力端子を設計インピーダンス(Z0)で終端したときの入出力インピーダンスと電圧利得(＝Sパラメータ)を示します。アッテネータを構成する抵抗の値はインターネット上に多くの計算ツールがありますのでそちらを参照ください。筆者は自身で計算テーブルを作成しているので使う機会がありませんが、Googleで検索して出てきたURLをご紹介しておきます。
(アッテネータ計算サイトの例)
https://www.trance-cat.com/electrical-circuit-calculators/pi-attenuator-calculator.php
http://gate.ruru.ne.jp/rfdn/Tools/AttForm.asp
http://www15.plala.or.jp/gundog/homepage/densi/keisan/att/att.html

この回路は入出力が完全に対称なので、S11=S22, S21=S12となり、各端子から相手側を見たインピーダンスは50Ω、利得は約0.708(=1/√2　すなわち-3dB)です。

このアッテネータの負荷側を開放にすると、電源側から負荷を見たインピーダンスは何Ωに見えるでしょうか?図1の②に示すようにS11’=約151Ωになってしまいます。’をつけているのは、便宜上S11と表現していますが、入出力がZ0で終端されていないので厳密にはSパラメータと呼べないためです。S21, S22についても同じです、負荷端を開放すると減衰比も代わってしまう…回路を見れば自明ですね。この計算は簡単ですので興味のある方はご自身で計算してみてください。

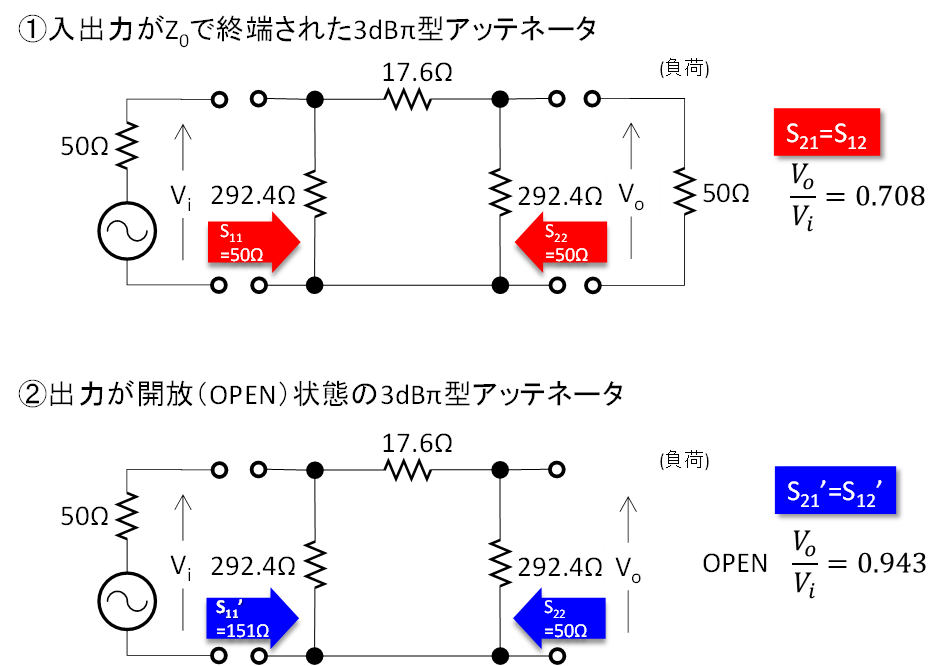
図1　3dBのπ型アッテネータで考えてみる

このように四端子回路網(デバイス)の入出力インピーダンスは、相手側端子の終端インピーダンスが変化すると変化するものなのです。そして変化する度合いは入出力の結合が大きい回路(デバイス)、言い換えると|S21 |×|S12|が大きい回路ほど大きくなります。

従って、図1のアッテネータの場合、減衰量が大きく(例えば20dB)なると相手側の端子を開放/短絡しても、入力インピーダンスはあまり変化しなくなります。

2. Sパラメータで表現すると

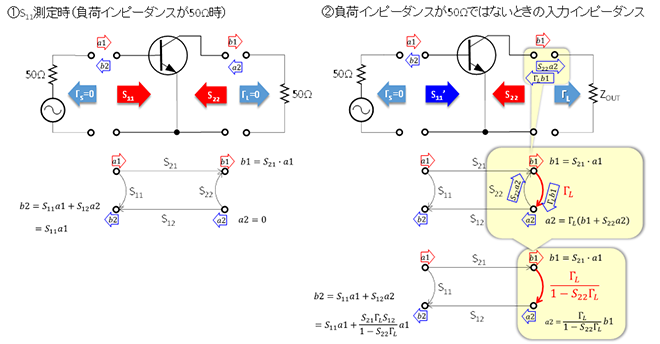
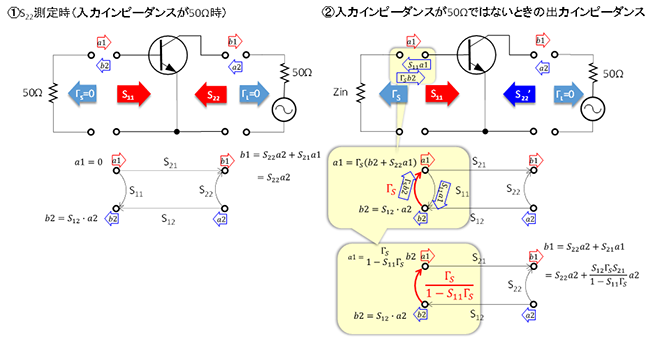
1章で述べた“そもそも”の話をトランジスタとSパラメータの話に戻すと図2のようなイメージになります。(A)は負荷インピーダンスがZ0ではなくなったときの入力端子(B-E間)の反射波の変化、(B)は入力インピーダンスがZ0ではなくなったときの出力端子(C-E間)の反射波の変化を示したものです。入射波と反射波の関係を判りやすくするために、別々の図にしましたが、実際には(A)と(B)は同時に発生していて重なった状態で観測されます。

(A)負荷抵抗が50Ωでないときの入力反射係数

(B)入力抵抗が50Ωでないときの出力反射係数

図2　図1をトランジスタとSパラメータで表現する。

ここでは図2(A)を例にとって解説します。トランジスタの入力反射係数Γin(=入力インピーダンス)は入射波a1と反射波b2の比、すなわちΓin=b2/a1となります。入力端子にインピーダンスZ0の電源を接続した場合に四端子回路網の入力端子に発生する反射波b2は、入力端子で反射された波(S11･a1)以外に出力端子で反射されて入力端子まで伝わってくる成分(S12･a2)が存在し、これらの和となります。図2(A)①に示すように、Sパラメータを測定するときは出力端子をZ0で終端するので出力端子に観測される負荷からの反射波a2は0です。(Z0で終端したときに発生する反射波を0と見なしていると理解した方が良いかもしれません) 従ってトランジスタの入力反射係数ΓinはS11となります。一方、負荷インピーダンスがZ0と異なる値の場合は図2(A)②に示すように、出力端子において以下の事が起こります。

1) トランジスタに入力されて増幅された波 b1=S21∙a1 が負荷で反射されて、ΓL･S21･a1の大きさの反射波となる。

2) この反射波の一部はトランジスタの出力端子のS22で再度反射され、さらに再度ΓLで反射される…ので、最終的に出力端子の反射波の大きさa2は(式2-1)に示す通りとなる。

両辺をa2とb1に整理して

a2について解くと

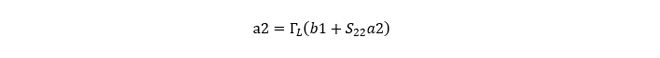
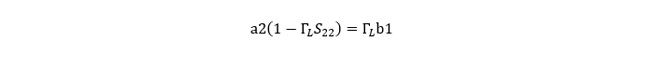
この出力端子に生じた反射波a2(出力端子から見ると入射波なのでaと表記)がS12倍されて入力端子に戻り、S11による反射波と合成されて入力反射波b2となります。すなわち

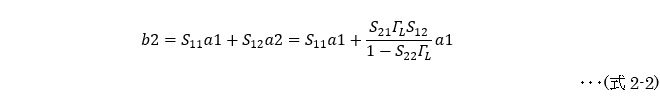
従って、この時のトランジスタの入力インピーダンスS11’は、

となります。出力インピーダンスについても入出力の関係が逆転するだけで考え方は同じです。図2(B)に示す通りの関係となり、出力インピーダンスS22’は、

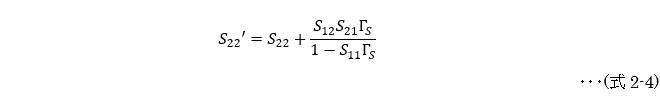
となります。第16話の図7、8はこれらの計算式をMicrosoft Excel®^※1で計算してMr.Smithに表示させたものでした。そして、1章でも述べた通りS12×S21が大きい程、反対側のポートの影響を強く受ける事が式からお解り頂けると思います。S12は出力ポートから入力ポートに向かう結合(逆方向伝達利得)、S21は入力ポートから出力ポートに向かう結合(順方向伝達利得)ですから、両者の積とは一方の端子に加えた振幅が他方の端子に伝達し、それが1往復して元の端子に現れるまでの利得を表します。

3. そもそもの話とトランジスタの関係

つまり四端子回路網においては伝達関数(Sパラの場合はS21とS12)がゼロでない限り、多かれ少なかれ、入出力のインピーダンスは相手ポートの影響を受けます。影響の度合いは、順方向伝達関数と逆方向伝達関数の積の大きさで決まり、順方向と逆方向の伝達関数が対称の場合は伝達利得の大きさが大きいほど、相手ポートの影響が強く表れます。

トランジスタの場合は順方向伝達利得S21が大きい(でなければ増幅しない)ので、相手ポートの影響が強く見えそうなものですが、逆方向の伝達利得S12が小さいので、入出力ポートは相互に干渉しない…というのが本来の姿なのです。(式2-3) (式2-4)にS12=0を代入するとS11’=S11、 S22’=S22となります。これが理想トランジスタであり、第16話でご説明した整合回路の設計法は、理想トランジスタを前提とした設計方法なのです。表1にここまでの話を整理しておきます。

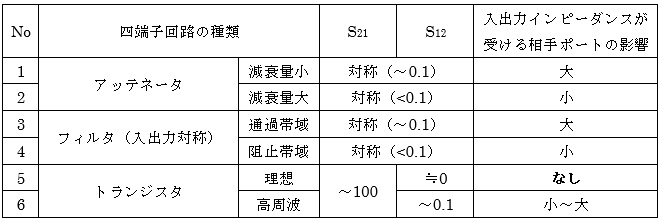
表1　伝達関数と入出力インピーダンスの関係

4. 厳密な入出力整合

では負荷インピーダンス、信号源インピーダンスの大きさで、入出力がお互い動いてしまうS11’、S22’に対して、どうやって整合回路設計すればよいのでしょうか?

S11’、S22’に対するそれぞれの整合条件は、整合回路をトランジスタ側から見たインピーダンス(反射係数)ΓS、ΓLがそれぞれ

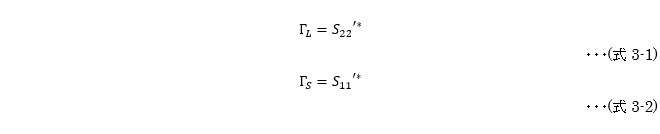
となる必要があります(*は共役複素数を示す)。整合条件は、これらの式と先に導出した(式2-3)(式2-4)の連立方程式を解く必要があります。結論のみ記載すると

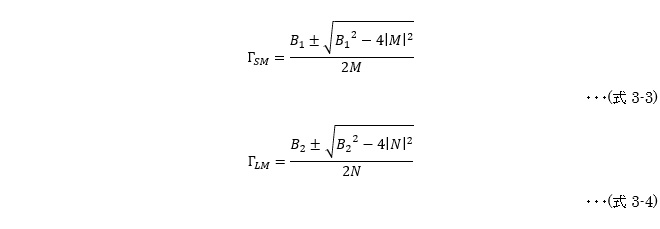
但し、ΓSM、ΓLM：入出力同時整合条件のΓS、ΓL、またB1、B2、M、Nはそれぞれ

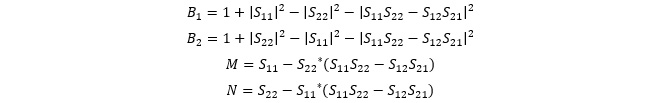
となります。^※2

非常に面倒ですがMicrosoft Excel®^※1で計算してみた結果を図3に示します。本図では検算のため、S12に0を代入した結果も重ねています。S12の影響がなければ、ΓSM＝S11*、ΓLM=S22*の関係(反射係数の虚数成分が±逆の関係)になっていることがお解り頂けると思います。

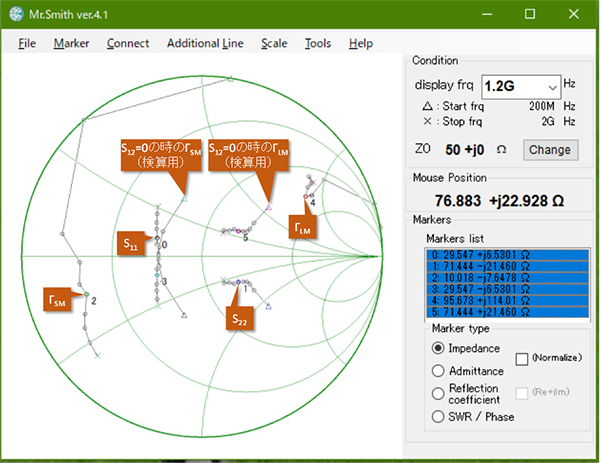
図3　入出力が同時に整合する電源／負荷インピーダンスの計算結果^※3

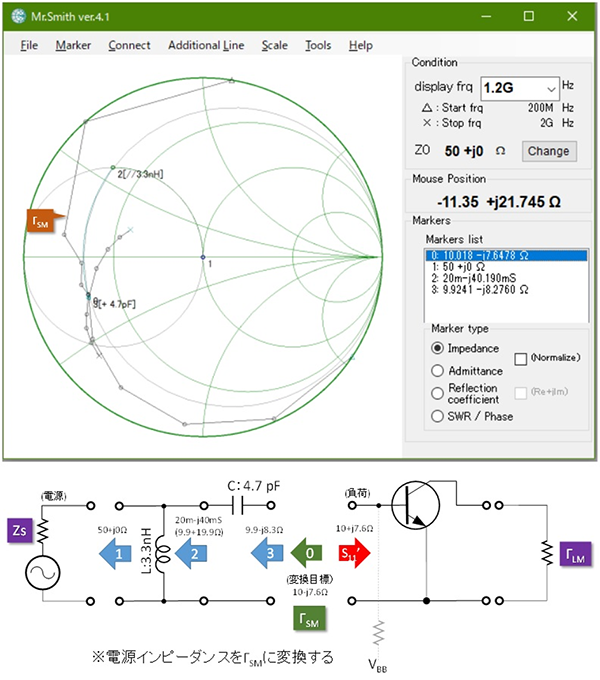
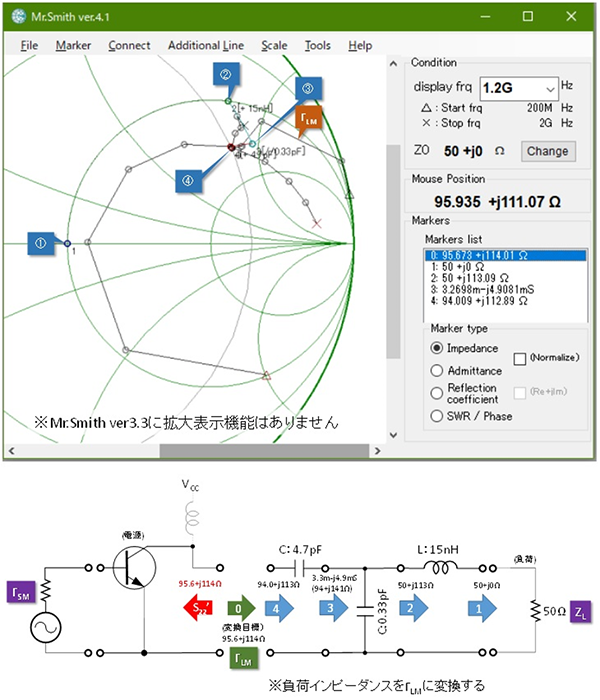
この計算結果は、トランジスタから見た電源、負荷の反射係数を示していますから、整合回路を設計する時は、「負荷インピーダンスを電源インピーダンスの複素共役に」ではなく、「入出力のインピーダンス(第16話の例では50Ω)をこの値(反射係数)に変換する」という操作を行います。第16話の図5、図6をΓSM、ΓLMで設計し直すと、図4、図5のようになります。^※4

図4　再設計した入力整合回路

図5　再設計した入力整合回路

第16話の図5、図6と比べると微妙にL, Cの諸元が変化していることがお解り頂けると思います。従来、実際の設計の現場においても、連立方程式は解かずにS11、S22に対して整合回路を設計し、試作品でこの程度のトリミングを実施すると言う設計はよく見かけます。

では、何故トランジスタの入出力整合回路を設計する時に、トランジスタの入出力インピーダンスをS11、S22として設計する手法が一般的なのでしょうか? 次回は、この理由について解説いたします。

5. 第17話のまとめ

今回は、トランジスタ増幅器の入出力インピーダンスが、何故相手ポートの影響を受けるのかと、これを考慮した整合回路設計を行う方法をご説明しました。要約すると以下の通りです。

(1) 四端子回路入力網の入出力反射係数(S11, S22)は、伝達係数(S21, S12)の大きさに応じて、相手ポートのインピーダンスの影響を受けます。
(2) トランジスタの場合、理想的にはS12≒0なので、入力インピーダンス=S11、出力インピーダンスS22として取り扱うが、実際の高周波トランジスタではS12が十分に小さい数字にならず、入力インピーダンス=S11、出力インピーダンスS22とならない。
(3) 入力インピーダンス=S11、出力インピーダンスS22とならない場合は、相手ポートの影響を考慮した入出力インピーダンス導出式で連立方程式を立てて、整合条件を求めるのが厳密な手法。

察しの良い方は図2を見てお気づきになったのではないかと思いますが、S12とは、トランジスタの出力が入力側にフィードバックされる大きさを示しています。従って増幅回路で、このパラメータが無視できないと言うことは、すなわち「発振しやすい」という事を物語っています。

単純に整合が難しいという問題に留まらないS12について次回以降も引き続き取り扱うことにします。なお、ご参考まで第16話の図7、図8の計算に用いたExcelシート、ならびに本話の図3の計算に用いたExcelシートを添付します。どうやって計算したかご興味のあるかたは参考にしてください。なお、これらExcelシートに関するご質問についてはご容赦ください。

これらExcelシートの内容に関する知的財産権その他一切の権利は筆者濱田倫一に帰属します。FB NEWS編集部は筆者濱田倫一の許可を得て本件記事を掲載しております。

また筆者、ならびにFB NEWS編集部は、これらExcelシートの二次使用に伴う一切の責任を負いませんので、あらかじめご了承ください。

※1　Microsoft Excel®は米国Microsoft社の登録商標です。
※2　(式3-1)~(式3-4)は、下記文献を参考に記載しています(一部引用)
Christian Gentili著 MIROWAVE AMPLIFIERS AND OSCILLATORS(McGrawHill) P33～P34
宮内一洋､山本平一共著通信用マイクロ波回路(電子情報通信学会) P191
※3　図3はMr.Smithの画面キャプチャを画像編集アプリで重ね合わせたものです。
Mr.Smithには3個以上の周波数軌跡を同時に表示させる機能はありません。
※4　Mr.Smith ver3.3のダウンロードはこちらから

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2020年3月号トップへ戻る

【第17話】増幅器とSパラメータ（その2）

1. そもそもの話

2. Sパラメータで表現すると

3. そもそもの話とトランジスタの関係

4. 厳密な入出力整合

5. 第17話のまとめ

NEWS

連載記事

テクニカルコーナー

JAIAコーナー

お知らせ

外部リンク