Mr. Smithとインピーダンスマッチングの話／【第9話】直列共振と並列共振　その2｜2019年7月号

Mr. Smithとインピーダンスマッチングの話

【第9話】直列共振と並列共振　その2

濱田倫一

第8話では前半で
・観測点から負荷までの距離（線路長）が有限の長さをもつ場合に、電源周波数の変化に伴って負荷インピーダンスがどのように変化するか
・理想のL、C、および理想のL、Cで構成された共振回路の周波数対インピーダンス特性をスミスチャート上で見るとどう見えるか
について解説しました。

後半では理想の回路素子と実際の回路素子の関係について説明し、実際のデバイスには「自己共振周波数」というものが存在する事を説明しました。

第9話では、デバイスメーカが開示するデータシートやシミュレーションモデルを使用して、実際のデバイスの自己共振周波数前後での振る舞いを見てみることにしましょう。

1. チップキャパシタの周波数対インピーダンス特性

セラミックキャパシタは使用している誘電体材料によって「高誘電率タイプ」と「温度補償」タイプがあり、前者は電源回路のバイパスコンデンサなど静電容量の精度よりも大容量を重視する用途、後者はRF回路のフィルタや整合回路など、静電容量の偏差や温度特性を重視する用途に使用されます。ここでは村田製作所のGRMシリーズから前者の代表としてGRM15x（1005サイズ）の1μFと2.2μF、後者の代表としてGRM18x（1608サイズ）の1000pFと0.01μFを例に採りました。図1～図2にGRM15xとGRM18xの代表データシートを示します。
（村田製作所のHPから転載：https://psearch.jp.murata.com/capacitor/lineup/grm/）

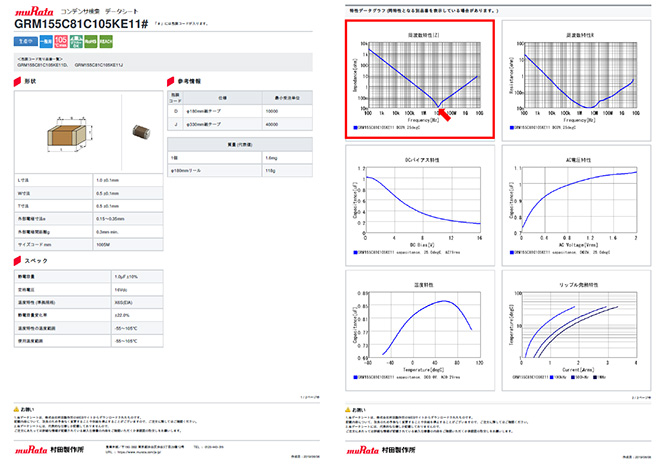
図1 高誘電率タイプセラミックキャパシタのデータシート（1μF、赤矢印が自己共振点）

https://psearch.jp.murata.com/capacitor/product/GRM155C81C105KE11%23.html
※2.2μFのデータシートは下記
https://psearch.jp.murata.com/capacitor/product/GRM155C81C225KE11%23.html

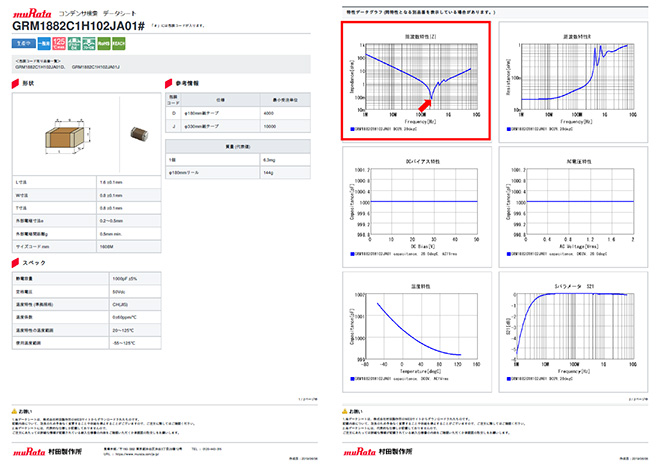
図2 温度補償タイプセラミックキャパシタのデータシート（1000pF、赤矢印が自己共振点）

https://psearch.jp.murata.com/capacitor/product/GRM1882C1H102JA01%23.html
※0.01μFのデータシートは下記
https://psearch.jp.murata.com/capacitor/product/GRM1882C1H103JA01%23.html

一般にセラミックコンデンサの個別のデータシートには「自己共振周波数」が項目として明記されていません。（総合カタログにシリーズ毎にまとめて記載されている場合が多い。）

個々の自己共振周波数の正確な値を知るには、図中に赤枠で囲った周波数対インピーダンス特性のグラフから矢印で指し示した直列共振点の周波数を読み取ります。自己共振周波数がわかれば、式（1）を用いて当該デバイスの寄生インダクタンスの大きさを求める事が可能です。

$f_{SR} = \frac{1}{2π \sqrt{C ∙ L_{P}}}, L_{P} = \frac{1}{{4π}^{2} {f_{SR}}^{2} C}$ 　--------------（1）

※fSR：自己共振周波数、LP：寄生インダクタンス、C：デバイスのキャパシタンス

最近ではメーカのHPからこれらの特性をCSVファイルでダウンロードできたり、回路シミュレータ用のデバイスモデルをs2p形式のファイルでダウンロードできたりと大変便利になりました。そこで赤枠で囲ったグラフのデータをCSV形式でダウンロードして1枚のグラフにまとめたのが図3です。左上の表は、グラフから読み取った自己共振周波数から式（1）で導出した寄生インダクタンスの大きさを示します。

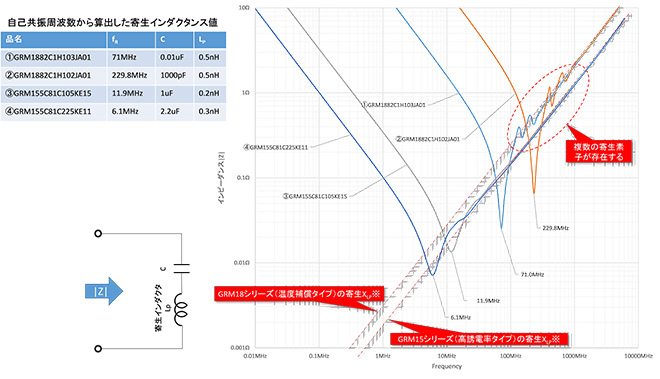
図3 各キャパシタの自己共振周波数と自己共振周波数から導出した寄生インダクタンス

図3を見るとチップコンデンサが集中定数のキャパシタ素子として機能している領域（グラフの傾斜が右下がりの区間）は各素子の容量が異なるので個別の場所にプロットされていますが、直列共振を経てインダクティブ領域に移行すると、GRM15、GRM18それぞれでグラフが重なっていることがわかります。これは寄生インダクタンスがデバイスの物理形状と端子間の電気長で決定されている事に由来しており、誘電体の材質と電極構造、ならびにチップサイズが同じだと、同じ値になる傾向を示しています。このように寄生インダクタンスの値がデバイスの物理サイズで概ね決定されるため、同一シリーズのデバイスにおいては、自己共振周波数はキャパシタンスの値が大きい程低くなる傾向を示します。

また材料が同じならチップサイズが大きくなる程共振周波数は低くなり寄生インダクタンスも大きくなる傾向と考えられます（図3においても1005サイズのGRM15xの方が寄生インダクタンスが小さい傾向にある）。このことは、昨今の無線機器の高周波化が半導体デバイスの進化のみならず、L、C、Rの小型化に大きく支えられていることを物語っています。

なお、この結果は一般的な傾向を示すものであって、全てのGRM18xシリーズ、GRM15xシリーズの寄生インダクタンスがそれぞれ同一であることを示すものではありません。（著者は全てを調べたわけではありません）

2. パスコンの並列接続を考察する

アナログ回路・ディジタル回路を問わず、電源回路のバイパスコンデンサには経験的に複数の容量を組み合わせるのが一般的ですが、これは前節で述べた自己共振周波数に対する対策で、低い周波数帯においては、自己共振周波数は低いが大きなキャパシタンスの（＝リアクタンスを小さくできる）デバイスが、高い周波数帯においては、キャパシタンスは小さい（周波数が高いのでリアクタンスは小さくなる）が自己共振周波数の高いデバイスがそれぞれ機能することを期待するものです。しかし実際には第8話で述べた通り、共振周波数の異なるデバイスを並列接続すると、それぞれの自己共振（直列共振）周波数の間に並列共振点が発生するため、その周波数帯ではバイパス回路の効果がなくなる事に注意が必要です。この様子を実際のチップキャパシタの並列接続で見てみましょう。

（1）実際のキャパシタの並列接続とインピーダンス軌跡
図４にGRM18xシリーズの0.01μFと1000pFを並列接続したときのインピーダンス特性を黄色の破線で示します。周波数の上昇に伴い、0.01μFが先に自己共振に達したあとL性領域に入り、これと1000pFのインピーダンス軌跡との交点が並列共振周波数となります。図4からは約177MHzと読み取れます。

図4　GRM1882C1H102JA01#(1000pF)とGRM1882C1H103JA01#(0.01μF)の並列接続

この並列回路のインピーダンスの変化をスミスチャート上で見るとどのように見えるのでしょうか。スミスチャート上の軌跡のプロットを図5に示します。

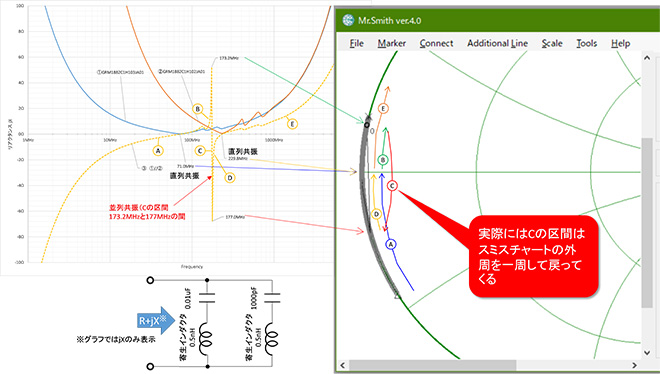
図5　図4のインピーダンス軌跡をスミスチャート上で見るとどう見えるか

図4は縦軸を｜Z｜としましたが、図5ではスミスチャート上のローカス（軌跡）との対応を判りやすくするために、縦軸をjXとしています。キャパシタの場合は損失が非常に小さいのが特徴で、スミスチャート上で見た周波数対インピーダンスローカス（軌跡）はスミスチャートの外周に張り付きます。但し外周を回転する速さは複雑で、周波数を低周波から高周波に一定速度でスイープすると、インピーダンスの軌跡は

①集中定数のCとして∞Ω（0Hz）から0Ωを目指して容量性領域の外周を時計方向に回転
（DC～71MHz:区間A）
②0.01μFの直列共振を経て誘導性領域の外周を時計方向に回転（71MHz～173.2MHz:区間B）
③ここから猛スピードでスミスチャート外周を時計方向に周り、途中∞Ωのポイント（並列共振点）を経て再び容量性領域に入り、1000pFの自己共振周波数付近で0Ωに近づく（173.2MHz～177MHz：区間C）
④1000pFの自己共振を経て（区間D）、周波数上昇と共に誘導性領域の外周を時計方向に回転（177MHz～ :区間E）
という経路を辿ります。つまり173MHzから177MHzの4MHzの間でスミスチャートをほぼ1周するのですが、図5ではダウンロードしたSパラメータのデータ間隔が広すぎて0Ω近辺を行き来しているように見えています。

同様に図4において並列共振周波数における|Z|が7Ω止まりになっていますが、これもデータ間隔の問題であって、実際には極狭い周波数帯で∞Ωまで達します。

（2）パスコン並列接続の真実
0.01μFに並列接続した1000pFは、本当に0.01μFのL性領域で端子間インピーダンスを下げるのに寄与しているでしょうか？

図6は図4の黄色の破線のプロットについて、インピーダンスの下がり方を考察したものです。
グラフを見ればお解りいただけると思いますが、0.01μF 1個に対して1000pF 1個の並列接続では、期待した0.01μFのL性領域でのインピーダンス低減効果は殆ど無く、並列共振によるインピーダンス上昇が目立ちます。これは、キャパシタンス比が1：10で、1000pFのリアクタンスが0.01μFと同じ大きさになるのは10倍高い周波数の時であるのに対して、自己共振周波数fSRの上昇は（LPが同じ大きさなので）倍でしかない為です。すなわち、このグラフは1000pFの個数を増やす、またはもっと自己共振周波数の高い別のデバイスを適用しないと、並列接続した小容量キャパシタのキャパシタンスによるバイパス回路の広帯域化はできない事を示しています。しかし、0.01μFも1000pFもインダクティブになった領域では（LPが同じ大きさなので）並列接続の効果からインピーダンスの値が半分になる結果、意外な形で減衰帯域が広帯域化しています。これがパスコンを並列接続して帯域が拡大する真の理由です。

図6　1000pFと0.01μFの並列接続でパスコン回路の減衰帯域はどう拡大したか

（3）寄生素子を含めたインピーダンスの計算方法
図4、図5の計算は、メーカが公開している同デバイスのSパラデータファイル（S2Pファイル）から、S11パラメータを抽出し、デバイス単体のインピーダンス数列に換算した上で、Mr. Smith ver4（目下制作中。未公開）で並列接続計算したものです。図4はその計算結果をテキストでExcelに貼り付けて｜Z｜計算し、結果をグラフにしています。

Mr. Smith ver4はまだ制作中で、公開中のMr. Smith（ver3.3）では、残念ながら直列回路の並列接続を周波数スイープして計算することができません。ADSやS-napのようなS2Pファイルを直接取り扱える高周波回路シミュレータが利用できない場合は、式(1)で自己共振周波数の値から寄生インダクタンスを導出し、第8話で紹介したような無償の回路シミュレータを利用して、図4に記載した等価回路のインピーダンスを計算する事で、ほぼ同様の解を得ることができます。

S2Pファイルと、そこから必要情報を抽出する方法については、次号でSパラメータのお話をする予定ですので、そのときに詳しく解説したいと考えます。

3. チップインダクタの周波数対インピーダンス特性

続いてチップインダクタの実例を見てみましょう。例に挙げるのは図6に示すTDKのMHQシリーズの1005サイズのチップインダクタ12nHと120nHです。これらのデータは村田製作所と同様、TDKのホームページからダウンロードすることが可能です。
URL：https://product.tdk.com/info/ja/products/inductor/inductor/smd/index.html

インダクタは基本的に巻き線構造の為、キャパシタと比較して端子間の電気長が長くなりやすく、自己共振周波数も低い傾向にあります。このため通常はデータシートの目につくところに自己共振周波数（SRF：Self-Resonant Frequencyと表記されている場合もある）の値が掲載されています。（図7の左側の赤枠部分）

図7　チップインダクタのデータシートの例（120nH）（赤矢印が自己共振点）

https://product.tdk.com/en/search/inductor/inductor/smd/info?part_no=MHQ1005PR12HT000
※12nHのデータシートは以下URLを参照
https://product.tdk.com/ja/search/inductor/inductor/smd/info?part_no=MHQ1005P12NJTD25

但し仕様値として記載されている自己共振周波数は幅を持った値で記載されているので、チップキャパシタの項で行ったように自己共振周波数から寄生キャパシタンスを算出するには、やはり周波数対インピーダンス特性のグラフからTyp値の自己共振周波数を読み取る必要があります。

図6の右側の赤枠で囲ったグラフが周波数対インピーダンス特性です。インダクタのインピーダンスは直流では0Ω（無損失の場合）で周波数の上昇に伴ってスミスチャートの誘導領域外周を時計方向に回転し、最初の自己共振は並列共振（スミスチャートの右端を通過）となるので、上に凸のグラフになります。赤矢印で示したピークがおおよその並列共振周波数です。

キャパシタの時と同様、12nHと120nHそれぞれのグラフのデータをダウンロードして、一つのグラフに重ねたのが図8です。1005サイズでこのあたりのインダクタンス値だと自己共振周波数が高く、10GHzまでのデータでは容量性領域のグラフが重なるところが見えませんが、自己共振周波数とインダクタンス値から寄生キャパシタの値を算出してみると、同図の表に示す通りインダクタンスの値が10：1の比率なのに対して、寄生キャパシタンスはほぼ同じ値になっています。

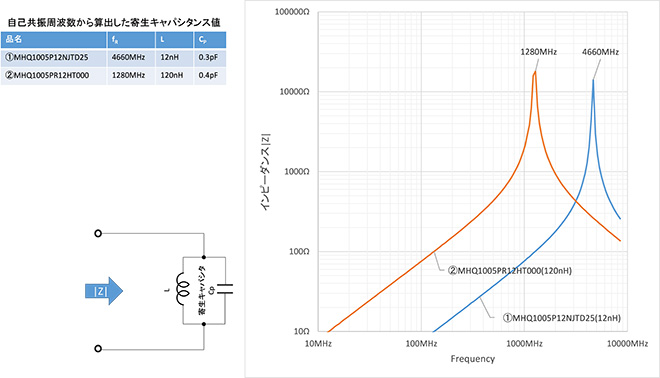
図8　各インダクタの自己共振周波数と自己共振周波数から導出した寄生キャパシタンス

（1）実際のインダクタの直列接続とインピーダンス軌跡
続いて自己共振周波数の異なるインダクタを直列接続したときのインピーダンス軌跡を見る事にしましょう。計算方法はキャパシタの時と同じく、ダウンロードしたS2PファイルからS11パラメータ数列を抽出し、デバイス単体のインピーダンス数列に換算した上で、Mr.Smith ver4（目下制作中。未公開）で直列接続計算しました。計算結果をテキストでExcelに貼り付けて｜Z｜計算した結果が図9の黄色の破線のグラフになります。周波数の上昇に伴い、120nHが先に自己共振に達したあとC性領域に入り、これと12nHのインピーダンス軌跡との交点が直列共振周波数となります。図9からは約3220MHzと読み取れます。

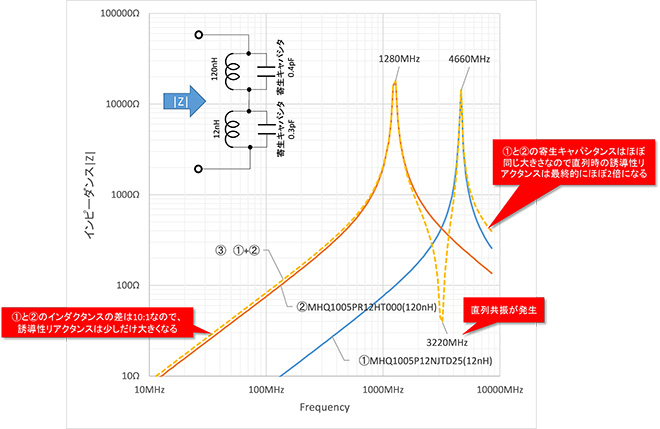
図9　MHQ1005PR12HT000(120nH)とMHQ1005P12NJTD25(12nH)の直列接続

この直列回路のインピーダンスの変化をスミスチャート上で見るとどのように見えるのでしょうか。スミスチャート上の軌跡のプロットを図10に示します。これも先程と同様、スミスチャート上のローカス（軌跡）との対応を判りやすくするために、周波数対リアクタンス(jX)特性のグラフと比較しています。キャパシタの場合と異なり、巻線構造を有するインダクタは損失が大きく、120nHが1.8Ω（データシートの「直流抵抗[typ.]」を参照）、12nHが0.19Ω、合計約2Ωの損失があります。この結果、チップインダクタの直列回路のインピーダンスローカスはスミスチャートの外周に張り付くことはありません。周波数を低周波から高周波にスイープすると、インピーダンスの軌跡は

①集中定数のL(132nH)として約2+j0Ω(＠0Hz)→12+j∞Ω(＠1280MHz)まで誘導性領域を時計方向に回転（区間A）※ Rが2Ωから12Ωに増加する理由は後述します。なお12Ωはj∞Ωのリアクタンスに対して十分に小さいため、この付近のインピーダンスローカスはスミスチャートの外周に張り付いて見えます。

②120nHが並列共振 12+j∞Ω → 12-j∞Ω(＠1280MHz)を経て容量性となり、12-j0Ω（＠3150MHz付近）まで容量性領域をほぼR=12Ω一定円に沿って回転（区間B）

③12nHと容量性となった120nHが直列共振 12-j0Ω→12+j0Ω（＠3150MHz付近）を経て再度誘導性となり、12+j∞Ω(＠4660MHz)まで誘導性領域をほぼR=12Ω一定円に沿って回転(区間C)

④12nHが並列共振 12+j∞Ω → 12-j∞Ω(＠4660MHz)を経て再度容量性となり、周波数上昇と共に容量性領域を時計方向に回転（4660MHz～ :区間D）

という経路を辿ります。直列共振周波数付近では少しの周波数上昇でリアクタンスが大きく変化しており、12+j0Ωの点を通過する軌跡が残っていませんが、実際の直列共振周波数は3080MHzから3220MHzの間にあり、この区間のインピーダンス軌跡は図10の赤の破線上を移動していると考えられます。

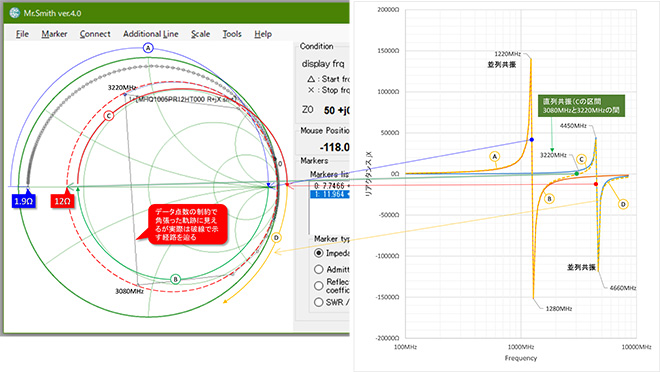
図10　図9のインピーダンス軌跡をスミスチャート上で見るとどう見えるか

（2）なぜ直列共振周波数ではRの値が大きくなるのか？
さて、各インダクタの等価直列抵抗RPがデータシート上では合計2Ωくらいなのに、120nHが自己共振を迎えた後に生じる120nH（実際はCに見えている）と12nHの直列共振周波数では、直列抵抗が12Ωに増大して見えました。なぜでしょうか。実はインダクタには直列抵抗以外にも損失性の寄生素子が存在しています。TDKはMHQシリーズの等価回路も公表してくれており、下記URLからダウンロードすることが可能です。
https://product.tdk.com/info/tvcl/ecm/inductor_automotive_high-frequency_mhq1005p_ecm.pdf

図11にこの等価回路を用いてMr. Smith Ver4.0を用いて計算した12nHと120nHを直列接続したときのインピーダンス軌跡を示します。Sパラメータで計算した図9の結果と比べるとR成分の大きさと共振周波数に若干の差異がありますが、概ね同様の軌跡になっていて、直列共振周波数はやや低めの3.05GHz、直列共振時のR成分（等価直列抵抗）は、やや高めの約19Ωとなっています。

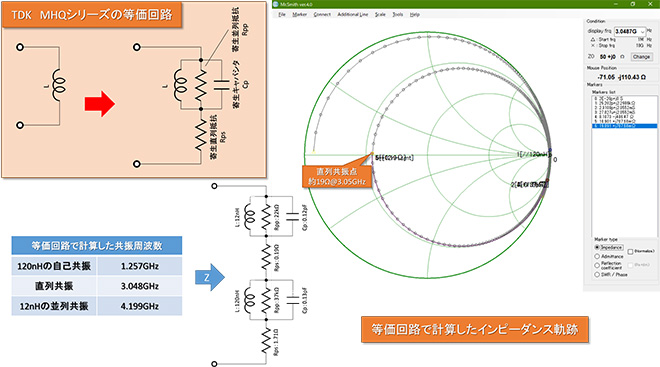
図11　MHQシリーズの等価回路と等価回路で計算した12nH+120nHのインピーダンス軌跡

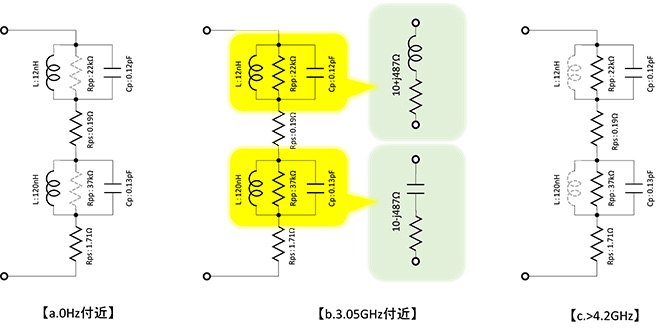
このR成分（約19Ω）の正体は、図11の左上に示した等価回路に記載されている寄生並列抵抗RPPです。巻き線構造を有するインダクタの損失は空間への磁束漏洩や巻き線の直列抵抗に由来する寄生直列抵抗RPSが支配的ですが、これ以外に巻き線の線間に生じる抵抗が存在し、等価回路上はインダクタの端子間に並列に挿入されます。図12a.に示すように、RPPは直流域では事実上インダクタで短絡された状態なので見えず、周波数の高い領域で影響が見えるのですが、リアクタンスjXLも大きな値になっているので、スミスチャート上ではその影響を簡単に目視することは困難です。

しかし直列共振状態ではリアクタンスが相殺して小さくなってくるので、スミスチャート上でも影響が見えるようになります。図12b.に示すように直列共振周波数付近では、黄色で示した部分のレジスタンス成分は、12nH、120nH共に約10Ω（この値はMr.Smith ver3.3で計算することが可能ですので、興味のある方は試してみてください）となり、両者が直列接続される結果、約19Ωの抵抗が見えています。直列共振点を超え、12nHの自己共振周波数も超えた領域では図12cに示すように、どちらのインダクタも容量性領域に入るので、RPPは常に見えるものの、今度はCPのリアクタンスが小さくなるので、やはりスミスチャート上では影響が見えなくなります。

図12　等価回路による計算結果

このように、損失性のある複数の共振回路を直・並列接続した回路のインピーダンスの周波数軌跡は構成される共振回路の数分だけ円を描きます。（ちょうど某電話会社のマークを90°回転したようなイメージでしょうか。）

4. さらに複雑なケース

最後に、自己共振周波数を超えてさらに高い周波数までインピーダンス軌跡を見た例をご紹介したいと思います。図13は、村田製作所製の0603サイズの120nHのチップインダクタLQP03HQR12H02のSパラメータ（S2P）ファイルから、単体のインピーダンスを導出してMr.Smithにプロットしたものです。LQP03HQR12H02の詳細は下記URLをご確認ください。

https://psearch.jp.murata.com/inductor/product/LQP03HQR12H02%23.html

このインダクタは4章で題材にしたTDKのMHQシリーズよりも若干自己共振周波数が高いのですが、並列共振後の容量性領域で小さな共振が2回発生しています。等価回路が開示されていないので、どのような寄生素子（回路）が存在するのか不明ですが、似たようなローカスが得られる回路として図12右下に黄色の四角で囲った領域に記載したような等価回路になるのではないかと想像します。本来のインダクタを構成する部分から、少し間隔をおいて並列に高い周波数で共振する構造が端子間に並列接続されているイメージでしょうか。本来のインダクタンスと寄生する共振回路を結ぶ寄生線路による共振（直列共振回路で表現）と寄生共振回路の共振がそれぞれ見えているように思われます。１章で題材にしたチップキャパシタでも似たようなインピーダンス特性が見えていますので、村田製作所のチップデバイス（パッケージ）構造に由来する特性なのかもしれません。

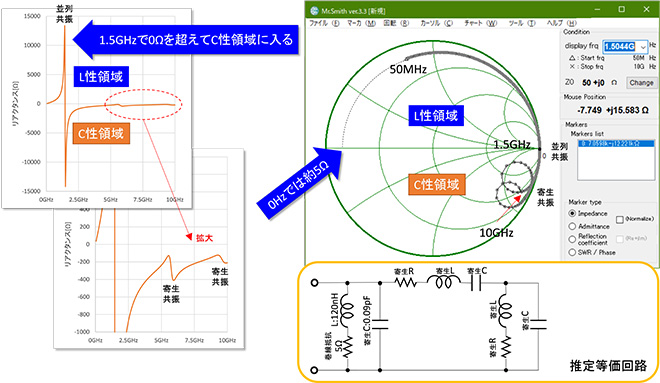
図13　LQP03HQR12H02#のインピーダンス特性と推定等価回路

5. 第9話のまとめ

第9話では、実際に市販されているデバイス（C,L）のインピーダンスの周波数軌跡をご紹介し、自己共振の実態と自己共振周波数が異なるデバイスを複数接続した場合のインピーダンス特性（周波数軌跡）について考察しました。要点をまとめると以下の通りです。

①　自己共振周波数からCの寄生インダクタンス、Lの寄生キャパシタンスを導出する方法を解説しました。
②　寄生素子の大きさは、同一シリーズ毎に同じ値をとるケースが多い。従って自己共振周波数は同一シリーズに於いては、その諸元が大きいものほど低い値を示す傾向になる。
③　電源パスコンにキャパシタンスの異なるキャパシタを並列接続すると自己共振周波数を超えて雑音抑圧帯域を広くすることができるのは事実だが、寄与する理由は自己共振前のキャパシタが機能しているからではなく、寄生インダクタンスが並列合成されて1/nになるためである。
④　共振回路が２つ以上組み合わされた回路のインピーダンスを周波数掃引して観察したとき、そのローカスはスミスチャート上に円を描く。
⑤　共振回路に並列の寄生抵抗が存在すると、直流域での等価抵抗と直列共振時の等価抵抗の値が異なる。（後者が大きくなる）

第9話では、分布定数回路（λ/4線路）やいろいろな「物」の共振についても触れようと思っていましたが、またしても力尽きてしまいました。今回、S2Pファイルが登場しましたので、次回はSパラメータのお話を先に行い、再び共振の残りのお話に戻りたいと考えます。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年7月号トップへ戻る