第10話では、Sパラメータの基礎について解説しましたが、第11話は再び「共振」の話に戻ります。第9話で実際の回路デバイスの自己共振についてご説明しましたが、共振するのはLやC等の電子デバイスだけではありません。スミスチャートを見ても判るとおり、電気長がλ/4を超える配線は共振特性を示します。第11話では伝送線路の自己共振と、これを積極的に回路素子として使用する「分布定数回路」について解説します。

1. 分布定数回路とは

(1) 第5話の復習
第5話で電源(インピーダンスの観測点)から電源までの距離が波長に対して無視できない長さになったとき、電源端における進行波に対する反射波の位相が負荷からの距離分だけ回転する結果、負荷端とは異なる値になることを解説しました。図1は第5話の図10を再掲したものです。

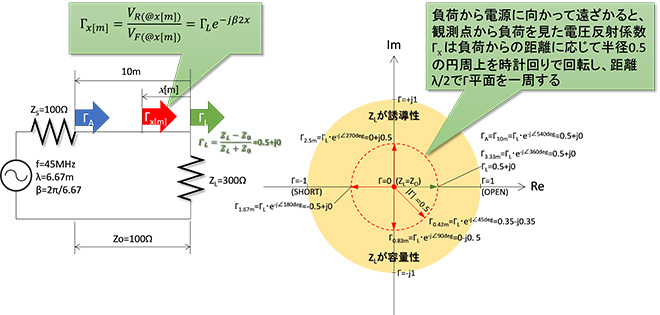
図1　線路長が波長に対して無視できない場合の反射係数Γの変化(第5話から再掲)

負荷抵抗と電源の距離が波長に対して無視できない大きさで離れると、電源から見た負荷インピーダンスは本来の負荷が純抵抗であるにも関わらず、両者を結ぶ伝送線路の長さによって、あたかもインダクタンスやキャパシタンスを接続したように見えます。一般に負荷抵抗(インピーダンス)ZLを特性インピーダンスZ0の伝送線路を介して電気長ℓ離れたところから観測した時のインピーダンスZinは(式1-1)で示されます。(但し線路が無損失の場合)

$Z_{in}=Z_0\frac{Z_L+j{Z}_0\tan \beta l}{Z_0+j{Z}_L\tan \beta l}$　　　但し $\beta =\frac{\mathrm{2\pi }}{\lambda }$（位相定数）   (式1-1)

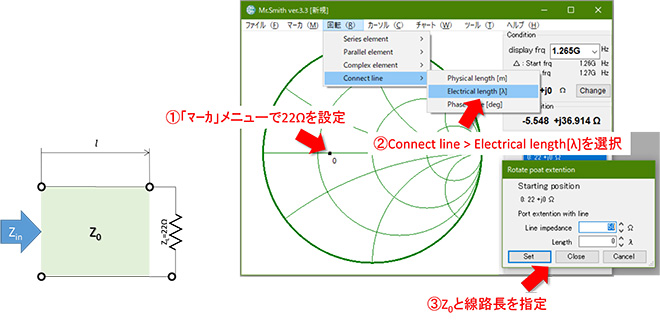
実際に任意の大きさのZLを任意のZ0の伝送線路を介して観察すると、インピーダンスはどのように変化するのでしょうか。ZL＝22ΩとしてMr.Smith^※1で計算してみましょう。計算方法は第6話で紹介しましたが、改めて図2に示します。

図2　伝送線路の接続計算

※1：Mr.Smithのダウンロードはこちらから

計算結果を図3に示します。ここではZ0＝10Ω、30Ω、50Ω、100Ωの4種類の線路で、それぞれλ/8(0.125λ)、λ/4(0.25λ)離れた点から観測したインピーダンスを計算しています。伝送線路を介してZLから遠ざかるとインピーダンスローカスは時計方向に円を描くように変化しますが、Z0<ZLの時は容量性領域に、Z0>ZLの時は逆に誘導性領域に向かう軌跡となります。なお、Z0=ZLの時は反射波の振幅が0になるので、インピーダンスの変化は発生しません(自明ですが…)

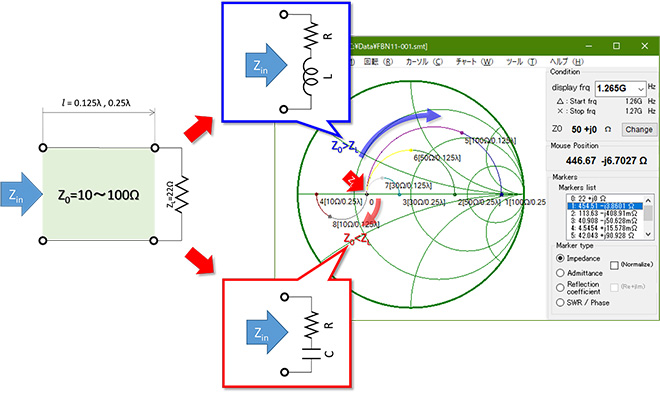
図3　22Ωを伝送線路を介してλ/8、λ/4離れた場所から観察

このように或る値のインピーダンスZLを伝送線路を介して観察すると、Z0とZLの大小関係でインダクタンス成分やキャパシタンス成分が見えます。そして線路長がλ/4の時、軌跡はZ0の値に関係なくスミスチャート上を180°回転しています。図3の例はここまでですが、さらにこの線路をλ/4延長すると、やはりZ0に関係なく180°回転し、合計λ/2の延長で元の値(図3の場合は22Ω)に戻るのは第5話でお話ししたとおりです。なおインピーダンスの軌跡が180°回転する点、360°回転する点において、その線路は共振状態にあります。この事は第12話で再度説明します。

(2) 分布定数回路とは
周波数が高くなってL,C,Rといったデバイスの大きさが波長に対して無視できない場合、言い換えると使用周波数がデバイスの自己共振周波数に近づいたり超えてしまったりする場合は、図3に示した伝送線路の振る舞いを利用して、インピーダンス変換や回路構成に必要なリアクタンスを実現する設計手法を採用します。任意の定数のデバイスを組み合わせて構成した一般的な回路を集中定数回路と呼ぶのに対して、伝送線路の特性インピーダンスと長さの組み合わせから所望のリアクタンスを実現して構成する回路を分布定数回路と呼びます。

2. 特性インピーダンスを変化させるには･･･

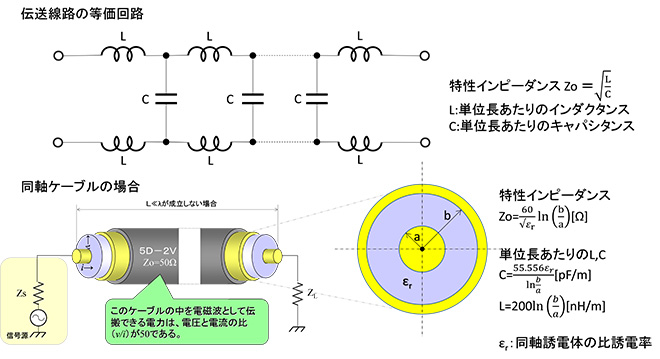
ここまで説明すると「Z0なんか自由に選べないでしょ！」と仰る方もおられるのではないでしょうか。第4話で説明しましたが、伝送線路の特性インピーダンスZ0は図4に示すように伝送線路(ケーブルなど)の断面構造で決まる諸元です。例えば同軸ケーブルの場合、市販品は50Ωか75Ωしか無く、これを変化させようとすると中心導体の太さや絶縁体の径を特注する必要が生じてしまいます。では分布定数回路に使用する伝送線路とはどのようなものなのでしょう。

図4　同軸ケーブルの特性インピーダンス(第4話から再掲)

(1) マイクロストリップライン
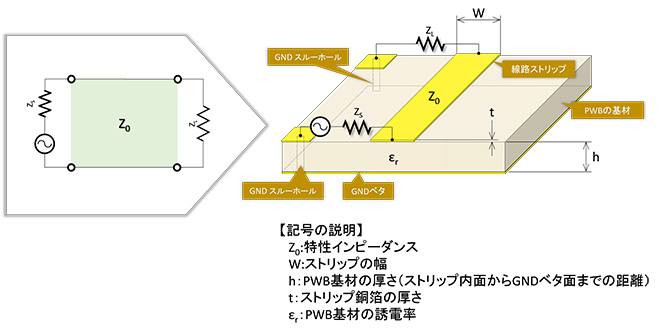
特性インピーダンスを自由に設計できる伝送線路の代表例は、プリント基板上に構成するマイクロストリップラインと呼ばれる伝送線路です。図5にマイクロストリップ線路の形状を示します。早い話がベタグランドの上に配置された配線パターンですが、これまで何度も述べた通り、特性インピーダンスを一定に保つために始点から終点まで、パターン幅、直下のGNDベタ面との間隔、周辺回路との距離などが常に一様の状態に保たれたものがマイクロストリップラインになります。

図5　マイクロストリップライン

図5において線路の特性インピーダンスは(式2-1)～(式2-8)で求められます。^※2

●W/h≦1の時
$Z_0=\frac{{\eta }_0}{2\pi \sqrt{{\epsilon }_e}}\ln \left(\frac{8h}{W\text{'}}+0.25\frac{W\text{'}}{h}\right)$　　　　　(式2-1)
●W/h≧1の時
$Z_0=\frac{{\eta }_0}{\sqrt{{\epsilon }_e}}{\left[\frac{W\text{'}}{h}1.393+0.667\ln \left(\frac{W\text{'}}{n}1.444\right)\right]}^{-1}$　　　　(式2-2)
●但し
$\eta =120\pi$　　　　(自由空間のインピーダンス)　　　　(式2-3)
●$\mathrm{W/h}\le \frac{1}{2\pi }$の時
$\frac{W\text{'}}{h}=\frac{W}{h}+\frac{125}{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}}\frac{t}{h}\left(1+\frac{4\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}W}{t}\right)$　　　　(式2-4)
●$\mathrm{W/h}\ge \frac{1}{2\pi }$の時
$\frac{W\text{'}}{h}=\frac{W}{h}+\frac{125}{\mathrm{\pi \; <!--\; greek\; small\; letter\; pi\; -->}}\frac{t}{h}\left(1+\frac{2h}{t}\right)$　　　　(式2-5)
${\epsilon }_e=\frac{{\epsilon }_r+1}{2}+\frac{{\epsilon }_r-1}{2}F\left(W/h\right)-\frac{{\epsilon }_r-1}{4.6}\frac{t/h}{\sqrt{W/h}}$　　　　(実効誘電率)　　　　(式2-6)
●W/h≦1の時
$F\left(N/h\right)={\left(1+12h/w\right)}^{-1/2}+0.04{\left(1-W/h\right)}^2$　　　　(式2-7)
●W/h≧1の時
$F\left(W/h\right)={\left(1+12h/W\right)}^{-1/2}$　　　　(式2-8)

※2：Bahl and P.Bharita, Microwave Solid State Circuit Design, Wiley, New York 1988から引用

(式2-1)、(式2-2)からは少々わかりにくいですが、基材の誘電率と厚さが一定の場合、ストリップ幅Wが大きく(パターンが太く)なるほど特性インピーダンスZ0は小さくなります。従ってプリント基板上ではパターン幅を変化させることにより、任意の値のZ0の伝送線路を作ることが可能です。

(2) マイクロストリップラインの設計ツール
同軸線路などと異なり、マイクロストリップラインの断面は線路の上下が非対称構造なので、線路断面の実効的な誘電率がPWB基材の誘電率よりも小さくなり、誘電体の厚さhとストリップの幅Wの比によって変化するため、設計は条件分岐を伴う少々複雑な計算となります。　かつてはPCや関数電卓に(式2-1)～(式2-8)の計算プログラムを仕込んで設計しましたが、昨今では下記URLのような計算サイトがあるので、計算式がわかっていなくても簡単に計算できてしまう便利な時代になりました。
①　https://keisan.casio.jp/exec/user/1223892753
②　http://www17.plala.or.jp/i-lab/tool/ms_line.htm
③　http://gate.ruru.ne.jp/rfdn/Tools/MstripForm.asp#
なおマイクロストリップラインの設計式には近似計算が含まれるため、いくつかの計算式が存在し、計算結果も微妙に差が出ます。上記3つのURLを比較すると、図5の条件では①→②→③の順にZ0が高くなる傾向がありました。

(3) 管内波長
これまで明確に区別すること無く解説してきましたが、伝送線路は一般的に線路を構成する(少なくとも)2つの導体･･･　同軸ケーブルの場合は外導体(シールド)と内導体(芯線)、マイクロストリップラインの場合はストリップパターンとベタGND　･･･を誘電体で支持して構成するため、自由空間よりも内部の波長が短くなります。自由空間の波長と区別する必要がある場合は、この伝送線路内の波長を「管内波長λg」と呼びます。どのくらい短くなるかと言うと、同軸線路の場合は誘電体の誘電率をεrとすると、
${\mathrm{\lambda \; <!--\; greek\; small\; letter\; lambda\; -->}}_g=\frac{\mathrm{\lambda \; <!--\; greek\; small\; letter\; lambda\; -->}}{\sqrt{{\mathrm{\epsilon \; <!--\; greek\; small\; letter\; epsilon\; -->}}_r}}$　　　　(式2-9)
となります。

マイクロストリップ線路上の波長(管内波長λg)は同軸ケーブルと同様、使用されている誘電体の影響で短縮されますが、同軸ケーブルのように断面空間全てに誘電体が存在する構造ではないため、線路断面の実効的な誘電率がPWB基材の誘電率よりも小さくなり、マイクロストリップ線路上の波長もその分長くなります。この実効的な誘電率が(式2-6)に示した実効誘電率εeです。従ってマイクロストリップラインの管内波長λgは、自由空間の波長をλとすると、
${\mathrm{\lambda \; <!--\; greek\; small\; letter\; lambda\; -->}}_g=\frac{\mathrm{\lambda \; <!--\; greek\; small\; letter\; lambda\; -->}}{\sqrt{{\mathrm{\epsilon \; <!--\; greek\; small\; letter\; epsilon\; -->}}_e}}$　　　　(式2-10)
となります。

図3で示したℓ=0.125λ、ℓ=0.25λ　の"λ"は管内波長λgの事を示していますので、物理長に換算する場合、同軸線路の場合は(式2-9)で、マイクロストリップラインの場合は、(式2-10)で計算する必要があります。

3. λ/4伝送線路によるインピーダンス変換

もう一度、図3を見てみましょう。長さℓがλ/4の伝送線路は、ある抵抗値から別の抵抗値にインピーダンス変換する働きがあります。進行波と反射波の位相差が変化してインピーダンスが変わって見える現象の応用なので、インピーダンスの変換に際して線路の長さℓが必ずしもλ/4である必要はないのですが、純抵抗から純抵抗への変換が可能なのは、インピーダンスローカスが180°回転する線路長ℓ＝λ/4の時とその奇数倍の時だけです。このためλ/4伝送線路はインピーダンス変換器(トランスと同等の動作)として分布定数回路では多用されます。λ/4伝送線路の特性インピーダンスZ0と入出力インピーダンスZS,ZLの間には(式3-1)に示す関係があります。

$Z_0=\sqrt{Z_s·\; <!--\; middle\; dot\; -->Z_L}$　　　　(式3-1)

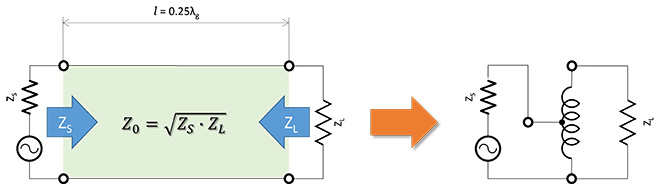
図6　λ/4インピーダンス変成器(右は等価回路)

(1) 50Ω－75Ωインピーダンス変換回路を分布定数回路で設計してみる
設計事例として、第二話で取り上げた50Ω－75Ωインピーダンス変換器をλ/4伝送線路で設計してみましょう。図7、図8は第2話で掲載した例題とその設計例の再掲です。

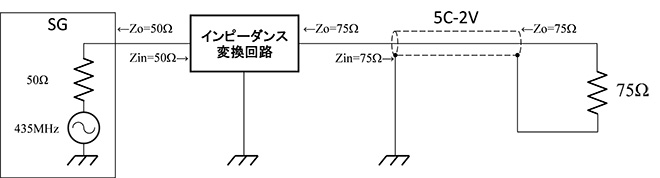
図7　50Ω－75Ωインピーダンス変換回路の定義(第2話から再掲)

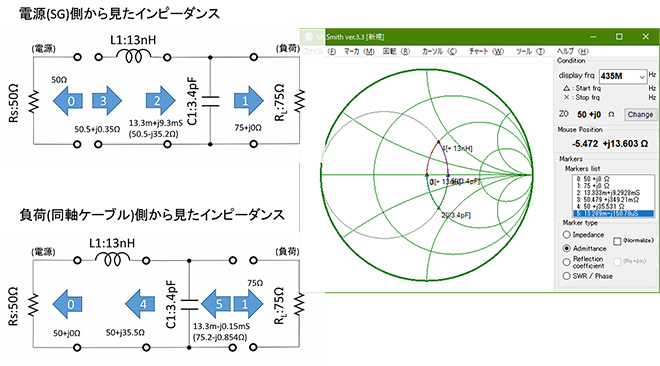
図8　集中定数回路での設計例(@435MHz、第二話から再掲)

同じ機能を分布定数回路で設計してみましょう。(式3-1)で変換回路を構成するλ/4伝送線路のZ0を計算するとZ0＝61.2372Ωとなります。Mr.SmithでZ0を振りながら、ちょうど良いところを探すという方法でも求められますが、簡単な計算なので、ここはZ0を直接計算した方が早いでしょう。50Ωの信号源にZ0＝61Ωの線路を接続してλ/4離れたところから見た信号源インピーダンスは図9に示す通り、74.4Ωとなります。

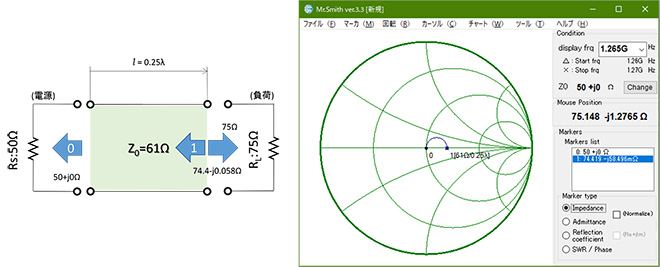
図9　分布定数回路での設計例^※3
※3　本例は1265MHzで計算していますが、長さをλで代入しているので、本結果に周波数依存性はありません。

(2) マイクロストリップ線路(パターン)の設計

では、この設計条件を満たすマイクロストリップ線路を1265MHzで設計してみましょう。プリント基板として、仕上がり厚さ0.8mm、銅箔厚35umのCEM3基板を使って設計してみます。設計は先に紹介したURL（https://keisan.casio.jp/exec/user/1223892753）で行いました。結果を図10に示します。

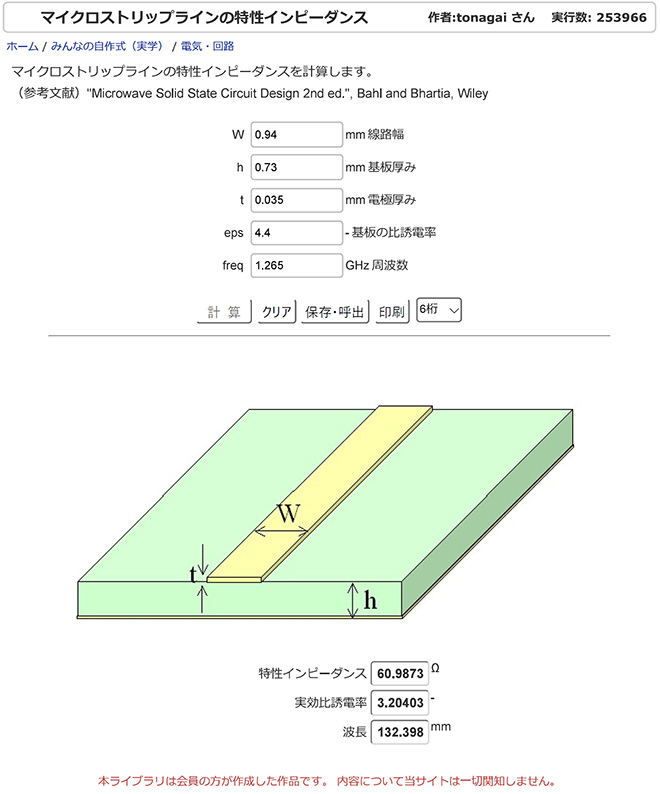
図10　マイクロストリップ線路の設計結果
（https://keisan.casio.jp/exec/user/1223892753　より引用）

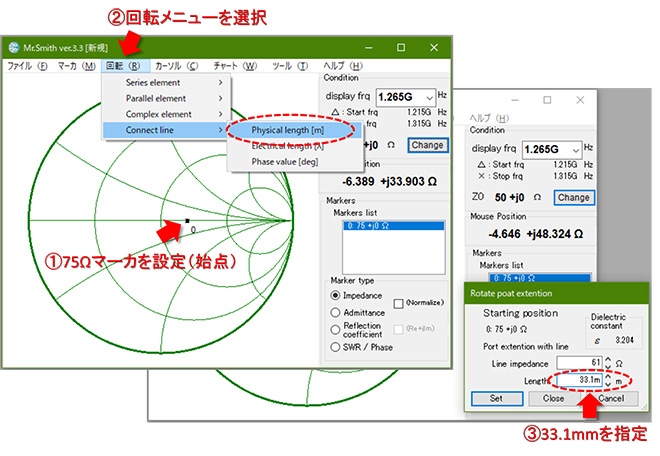
Z0＝61Ωのマイクロストリップ線路のストリップ幅Wは0.94mm、管内波長λg=132.4mmなので線路長33.1mmでλ/4となります。実際に製作したときのイメージを図11に示します。マイクロストリップ線路を折り曲げて配置すれば、もう少し小さくできると思いますが、1.2GHz帯では未だちょっと大きいですね。

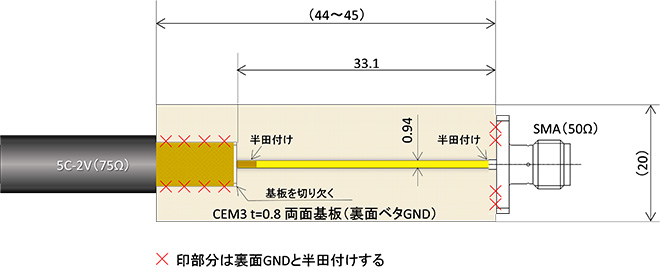
図11　インピーダンス変成器の完成イメージ

(3) 帯域特性の確認

最後に端数を丸めた影響とインピーダンス変成器の周波数帯域について確認しておきます。図12に示す通り、確認したい周波数帯域と計算点数(ここでは±500MHzで確認しました)、ならびに図10で計算した実効誘電率(実効比誘電率)を設定し、図13の手順で線路長33.1mmでのインピーダンスローカスを計算します。

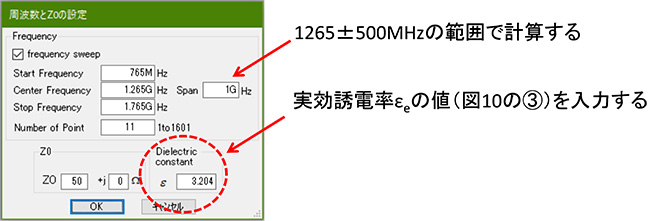
図12　誘電率の変更

図13　物理長を指定して再計算する

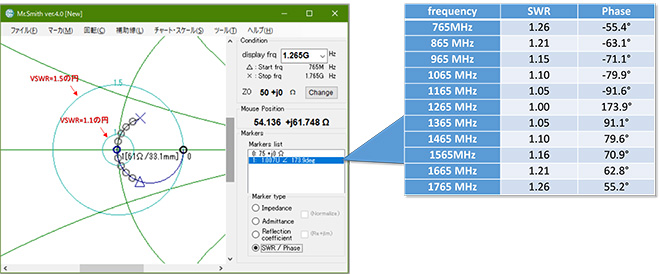
計算結果は図14に示す通り(画面の拡大図を挿入する都合上、Mr.Smith ver4.0(制作中)での計算結果を貼り付けています。Mr.Smith ver3.3には拡大表示機能はありません)、±100MHzの帯域においてはVSWR≦1.05、±200MHzの帯域ではVSWR≦1.10の性能となっています。

なおVSWR一定円は「チャート」→「SWR Curser」→「Draw」でポップアップメニューから大きさを指定できます。

図14　計算結果

4. 第11話のまとめ

これまでのλ/4線路のお話は負荷インピーダンスが純リアクタンスだったので、線路長の変化に伴うインピーダンスローカスの回転は、全てスミスチャートの最外周で発生しましたが、負荷インピーダンスがレジスタンスの場合には、線路の特性インピーダンスによって回転半径が変わり、λ/4線路がインピーダンス変成器として機能することをご理解いただけたかと思います。

要点をまとめると以下の通りです。

①　負荷インピーダンスZLを伝送線路を介して離れた点から観測した場合のZ’(本文ではZin)の大きさは、伝送線路の長さだけで無く特性インピーダンスによっても変化する。
②　インピーダンスローカスの回転は常に時計回りだが、回転方向はZL>Z0の時は容量性領域、ZL<Z0の時は誘導性領域に向かって回転する。
③　線路長がλ/4の時、軌跡の回転角度はZ0とZLの大小に関係なく180°となる。
④　①～③のような伝送線路の振る舞いを積極的に利用して構成する高周波回路を分布定数回路と呼び、デバイスの大きさが取り扱う信号の波長に対して無視できない場合に、常套手段として採用される設計手法である。
⑤　分布定数回路に適用するのに便利な伝送線路としてはマイクロストリップラインが代表的である。
⑥　のλ/4線路は、インピーダンスZSからZL(またはその逆方向)への変換器として動作する。

分布定数回路の歴史は古く、恐らくアンテナの給電回路に設けられたバランやスタブがその源流だと思います。また本格的に分布定数回路と呼べるものは導波管を用いた「立体回路」が最も古くから存在する分布定数回路ではないかと思います。分布定数回路で多用される概念は今回ご説明したλ/4線路によるインピーダンス変成とλ/4線路によるスタブ回路(またはチョーク回路)です。次回はスタブ回路を中心にお話ししたいと考えます。