Mr. Smithとインピーダンスマッチングの話／【第14話】<em><em>Q</em></em>とは何か(その2)｜2019年12月号

Mr. Smithとインピーダンスマッチングの話

【第14話】Qとは何か(その2)

濱田倫一

第13話では”Q”とは何か？と言うテーマで、QがデバイスのQ、共振回路のQ、回路の動作Qに分類できること、ならびにそれら相互の関係についてご紹介しました。第14話では実際のデバイスのQについてもう少し掘り下げて解説します。第9話で市販のキャパシタやインダクタのデータシートやSパラメータから自己共振周波数を調べました。今回も同様の方法を使って実際のデバイスのQの姿について調べてみることにします。

1. キャパシタのQ

キャパシタの等価回路は図1の左側に示すように、理想キャパシタCに並列に接続される絶縁抵抗R_Pと直列に接続される等価直列抵抗R_Sで表現されます。等価直列抵抗はESRとも呼ばれ、スイッチング電源を設計される方にはおなじみの諸元です。

図1の右側に示すQの定義で登場する直列抵抗Rは、R_SとR_Pを合成して直列抵抗に換算した値になるのですが、最近のキャパシタは絶縁性能が高く、R≒R_Sとして取り扱えることもあります。回路電流が小さく、R_Pが無視できない場合はQよりもtanδで損失を表現するケースが多くなります。

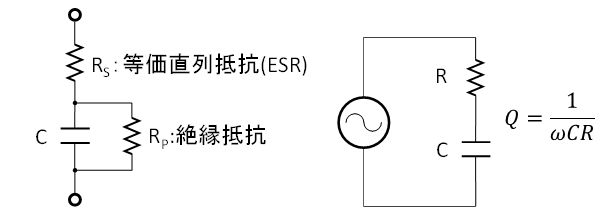
図1　キャパシタの等価回路(左)とQの定義

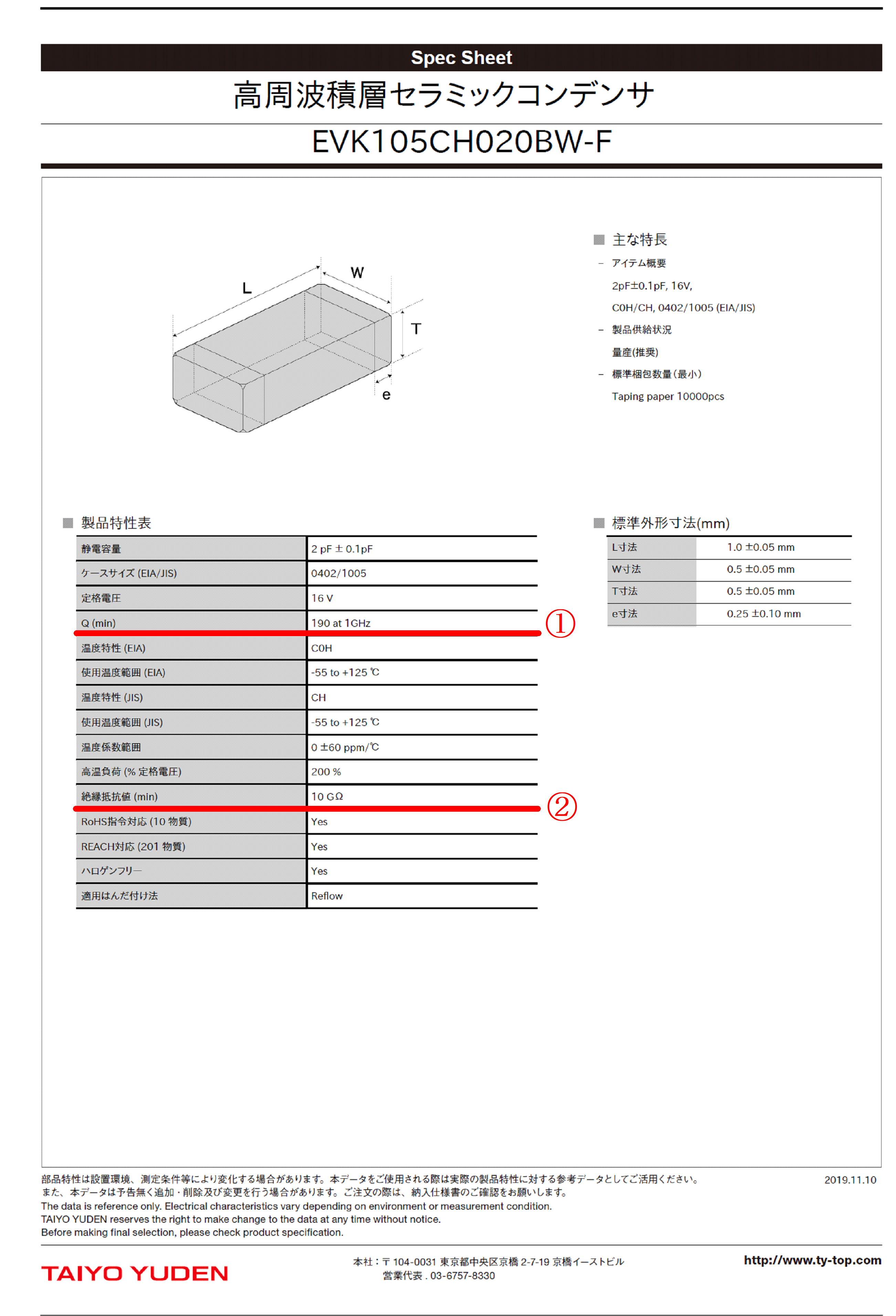
ここでは太陽誘電(株)製の1005サイズチップキャパシタEVK105CH020_W-F(2.0pF)を例にとることにします。図2～3にデータシートのコピーを示します。図2に赤く①と記した項目がQで、Qmin=190@1GHzと読み取れます。従って図1右側の定義から直列損失Rは

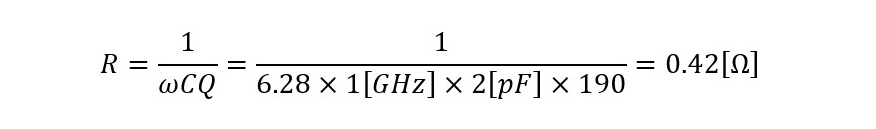
･･･ (式1-1)

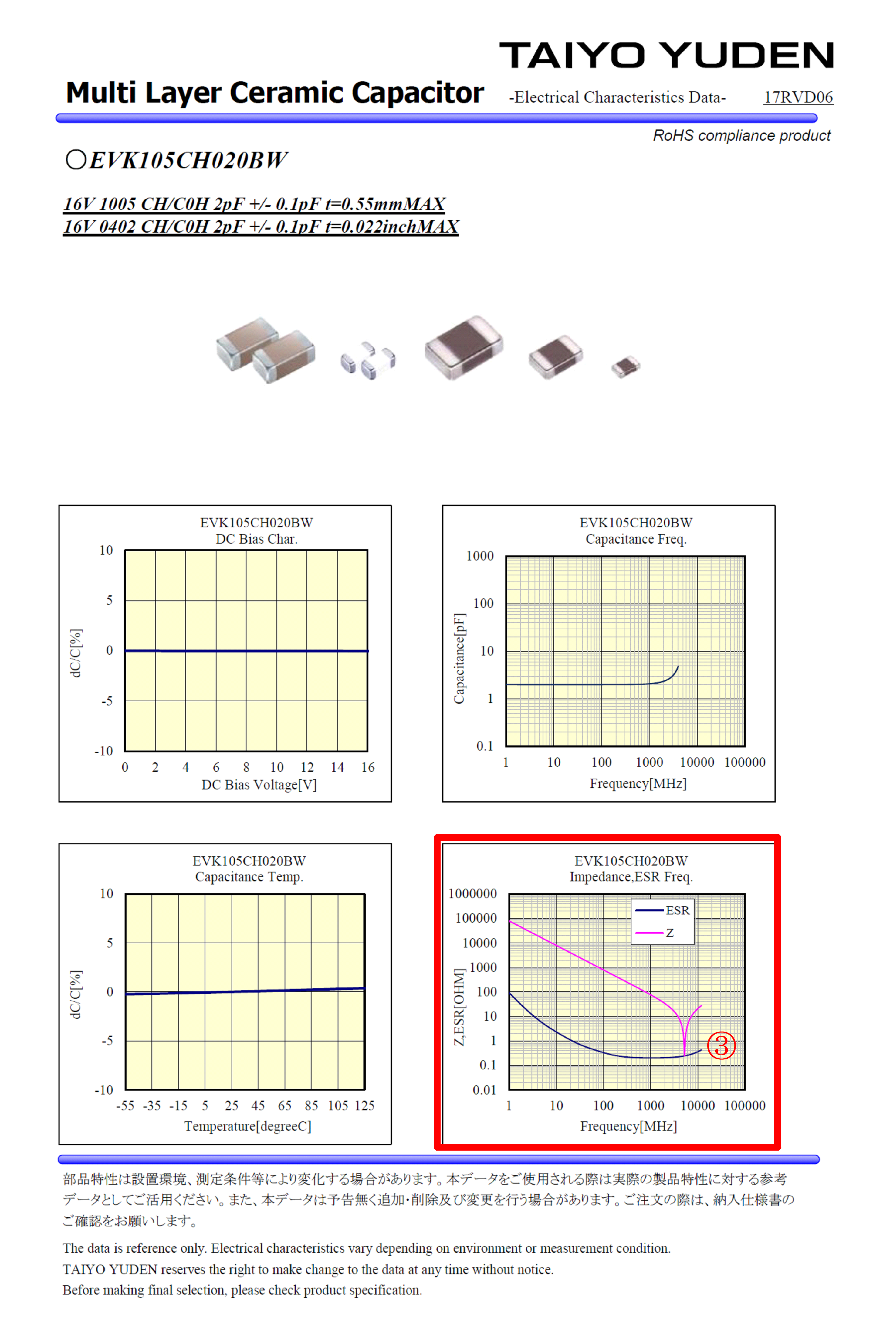
と算出されます。Qが最小値(min)なのでRは最大値という解釈になります。本来抵抗値は周波数が変化しても値は変化しないので、キャパシタのQの値は周波数が高くなるほど値が小さくなる傾向を示します。ちなみに図3の③は図1の左側の図に書かれているESRの周波数特性を示すグラフで、1GHzにおけるESRは0.2Ωと読み取れます。Q値から算出したRの値と比較すると倍/半分の違いです。

図2　太陽誘電 EVK105CH020BW-Fのカタログ

https://ds.yuden.co.jp/TYCOMPAS/jp/detail?pn=EVK105CH020BW-F&u=M

図3　太陽誘電 EVK105CH020BW-Fのカタログ

https://ds.yuden.co.jp/TYCOMPAS/jp/detail?pn=EVK105CH020BW-F&u=M

次に、メーカから公開されているデバイスのSパラメータからRの値を読み取ってみましょう。結果は図4に示すとおりです。Mr.Smithを使用して、s2pファイルからデバイスのインピーダンスを求める方法については、第10話の「3．S2Pファイル(Touchstone format)とは」で解説していますのでそちらを参照してください。

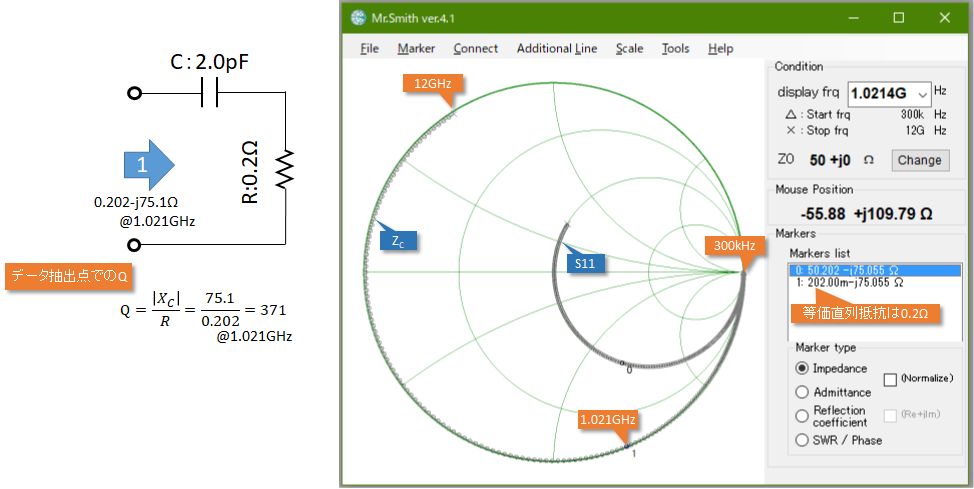
図4　太陽誘電 EVK105CH020BW-FのSパラメータから導出したRの値

Sパラメータから読み取った直列抵抗Rの値は図2の③で示すESRの値と概ね一致しています。ちなみに図1の②に示した絶縁抵抗値(Rp)が10GΩなので、これを直列損失に換算してもこのQminから導出したRの値とSパラメータから導出したR(＝ESR)の差分を説明するには足りません。

2. インダクタのQ

次にインダクタのQを見てみましょう。インダクタの等価回路も図5の左側に示すように、理想インダクタLに並列に接続される巻線間絶縁抵抗R_Pと直列に接続される等価直列抵抗R_Sで表現されます。等価直列抵抗は巻線の導体抵抗でR_Pは巻線の絶縁被膜の抵抗になります。

図5の右側に示すQの定義で登場する直列抵抗Rは、キャパシタの時と同様、R_SとR_Pを合成して直列抵抗に換算した値になるのですが、UHF帯以上の周波数で使用されるボビンレスの空芯コイルなどの場合は巻き線間が密着しないのでR≒R_Sとして取り扱えることもあります。インダクタの場合はそもそも端子間絶縁性のないデバイスなので、tanδで損失を表現するケースは殆どありません。

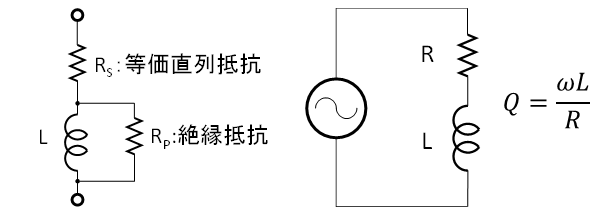
図5　インダクタの等価回路(左)とQの定義

ここではCoilcraft製の表面実装型空芯コイル0908SQ8N1(8.1nH)を例にとることにします。図6にデータシートのコピーを示します。図6に赤く①と記した項目がQで、測定周波数は②の部分に記載されており、Qtyp=130@400MHzと読み取れます。従って図5右側の定義から直列損失Rは

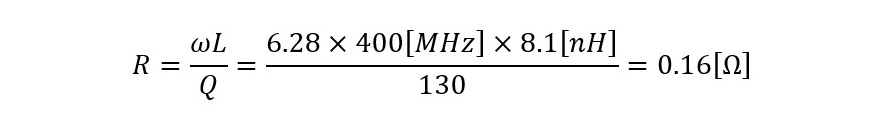
･･･ (式2-1)

と算出されます。Qが標準値(typ)なのでRも標準値という解釈になります。本来抵抗値は周波数が変化しても値は変化しないので、インダクタのQの値は周波数が高くなるほど値が大きくなる傾向を示します。

図6　Coilcraft 0908シリーズのカタログ

https://www.coilcraft.com/pdfs/sq_spring.pdf

キャパシタの時と同様、メーカから公開されているデバイスのSパラメータからもRの値を読み取ってみましょう。結果は図7に示すとおりです。やはりQから算出した値との間に大きな開きがあります。

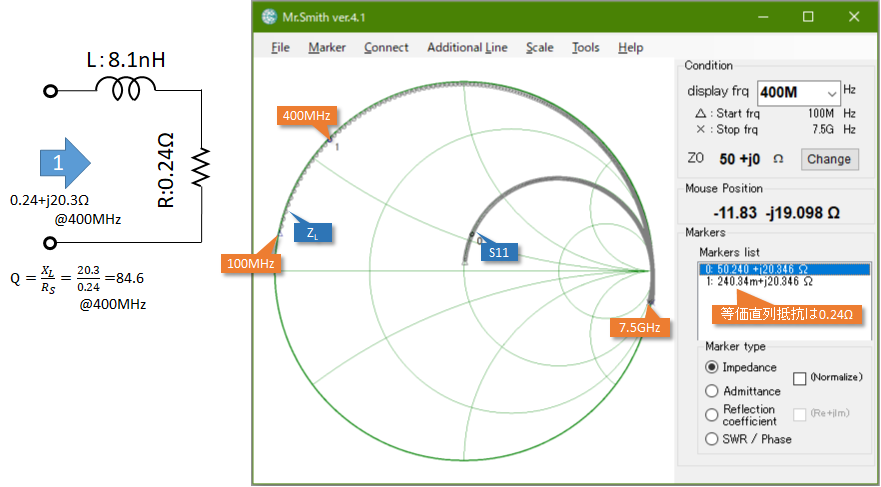
図7　Coilcraft 0908SQ8N1のSパラメータから導出したRの値

3. Qの精度

ここまでの結果をまとめてみます。

	Qから算出したR	Sパラメータから算出したR	その他の関連する諸元
キャパシタ	≦0.42Ω	0.2Ω	ESR=0.2Ω@1GHz
インダクタ	0.16Ω	0.24Ω	DCR＝6mΩmax^※1

※1：図6の③より引用

それにしてもバラバラの結果になりました。
経験的には、デバイスのQ(ならびに損失抵抗R)やESRの値は周波数特性に線形性がなく、かつ測定方法や導出方法による偏差が大きい諸元です。従って設計に使用するときは、倍/半分のばらつきを想定する必要があると考えます。以下、なぜそうなるのかについて説明します。

(1) 仕様値(min値)と標準値(typ値の違い)
キャパシタのQ値(図2の①)から算出したRがSパラメータから算出したRよりも大きな値になっている理由は、使用したQの値が仕様上の最小値(実際の測定値ではなくマージンを含んだ値)であることに起因していると考察します。Sパラメータから導出したRと等価直列抵抗ESRの値はよく一致しており、設計に使用する諸元としてはこの値を採用するのが妥当だと考えます。(恐らくメーカはESR値をSパラメータから算出していると想像します→同一の値)

(2) 自己共振の影響
図8は今回のインダクタのSパラメータデータファイルから抽出した周波数対インピーダンス特性(左)と周波数対アドミタンス特性(右)のグラフです。第13話「共振回路のQ」で説明した等価回路であれば、共振回路に挿入されたR(G)成分は周波数が変化してもその値が変化することは無いはずなのですが、自己共振周波数において、Rのグラフにも共振のピークが確認できます。

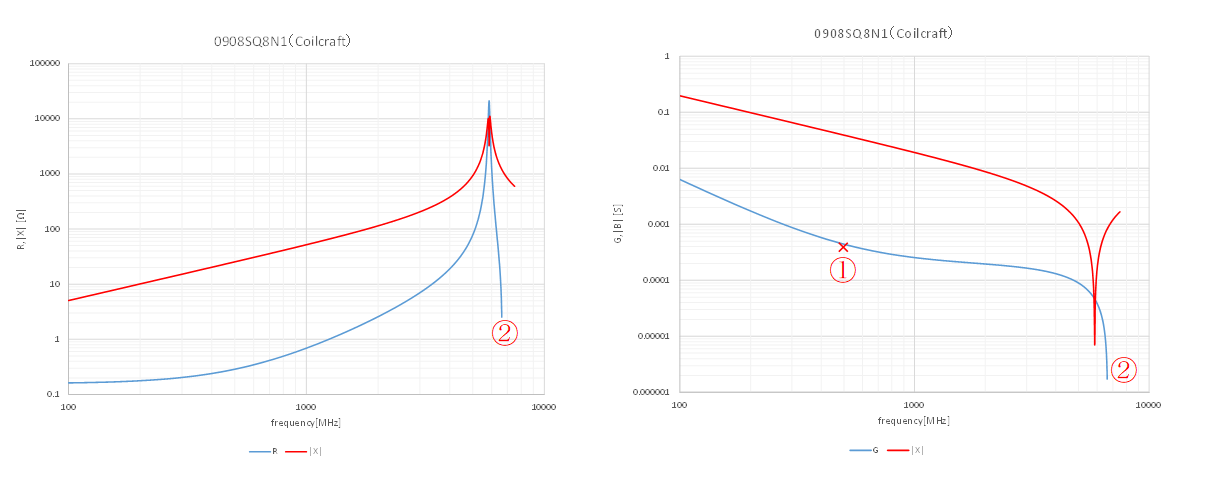
図8　Coilcraft 0908SQ8N1のSパラメータから導出したインピーダンス(左)とアドミッタンス(右)の周波数特性^※2

※2：リアクタンスのピークが2つあるように見えているのはグラフのサンプリング間隔の都合で絶対値にへこみが生じたもので、実際にはピークは1点です。

これはインダクタの最初の自己共振が並列共振となるため、損失を直列抵抗(レジスタンス)として観測すると共振周波数付近でRの値が変化して見えてしまう事に起因します。ここでは図9、図10で視覚的に説明します。今回サンプルに用いたCoilcraftの0908SQ8N1は図6からおおよそ3.96GHzで自己共振しています。従って損失をGで表現した場合の等価回路は図9、図10に示すような構成になります(損失コンダクタンスGは図8から読み取った値でざっくり0.2mSとしています)。並列共振においては、周波数スイープしたときの反射係数のローカスはアドミッタンスチャートの定G円上に現れます。従って図8に示すように、理想状態においては周波数対アドミッタンスのグラフを見ると共振周波数付近においてもGは変化しません。この時のQは

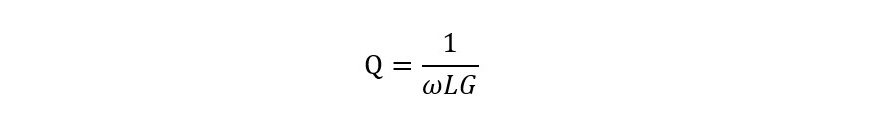
･･･ (式3-1)

従ってCoilcraftのカタログ値Q=130typ@400MHzから損失Gを計算すると

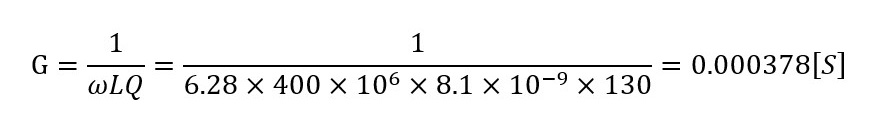
･･･ (式3-2)

約0.4mSとなり、図7の①で示すあたりとなります。グラフの読み値が約0.45mSなのでそこそこ一致しています。但し図7の右側のグラフに表示されているGの値はお世辞にも一定値とはいえません。これについては(3)で考察します。なお、図7の②で示した落ち込みはR､G共に同じ方向に発生しており、共振に伴う変動とは別の理由によるもの(測定上の何らかの問題)と考えられます。

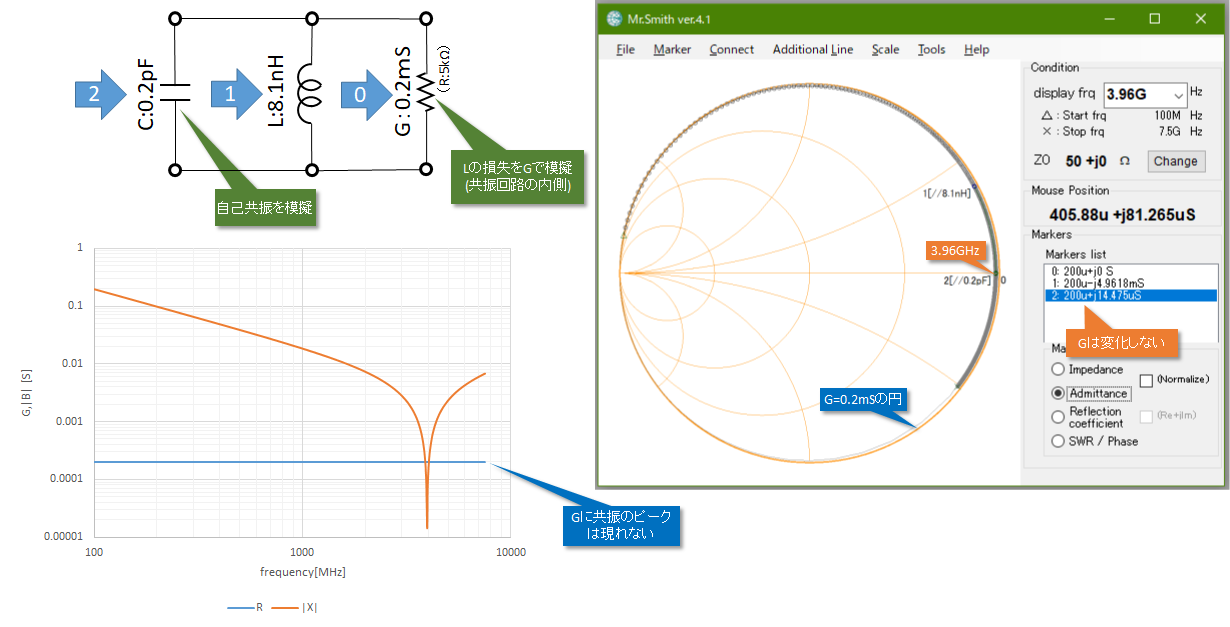
図9　並列共振(損失をGで表現)したときの周波数対アドミタンス特性

同じローカスをインピーダンスとして読み取ったときの結果が図10になります。チャートの右端でローカスが定R円の内側に入るとあたかも共振特性のような抵抗値のピークが見えるようになります。

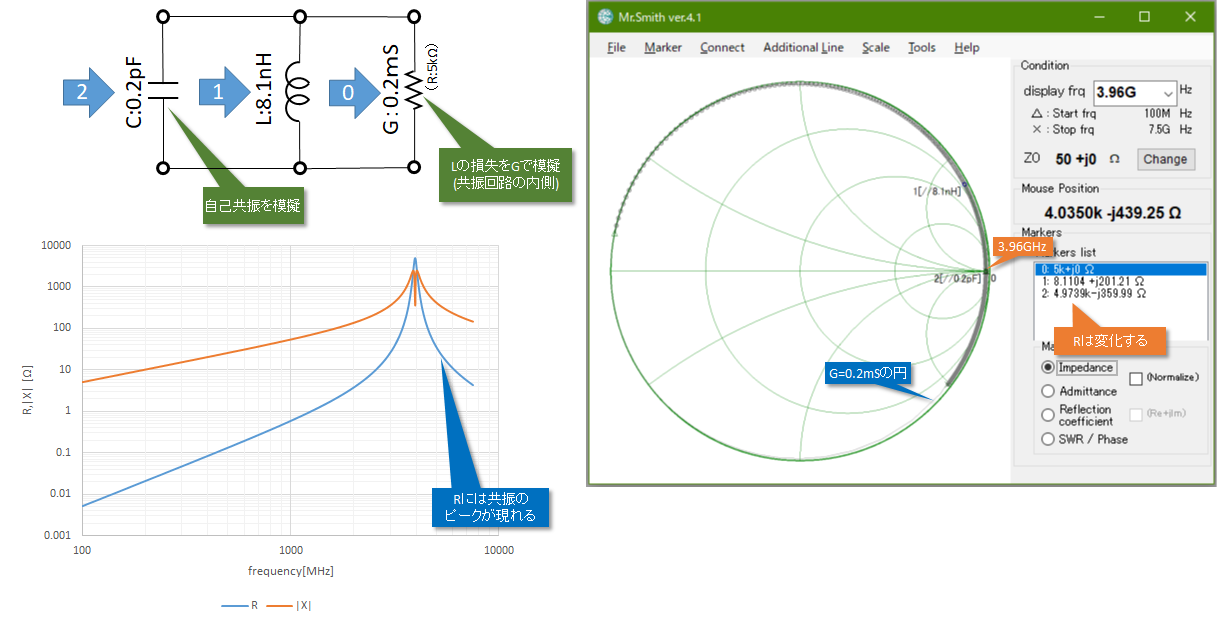
図10　並列共振(損失をRで表現)したときの周波数対インピーダンス特性^※3

※3：リアクタンスのピークが2つあるように見えているのはグラフのサンプリング間隔の都合で絶対値にへこみが生じたもので、実際にはピークは1点です。

(3) 測定精度の限界
図7右側のグラフを見ると、アドミッタンスとして評価してもGのグラフは図8に示すような一定値にはなっていません。また②で示した箇所はB成分の共振ピークと異なる周波数でマイナスピークらしきものが現れています。この周波数では左側のRのグラフにも②と記していますが、同様に落ち込んでいます。これらは測定精度が悪くて、本来存在しないピークの可能性があります。スミスチャート上を回転する反射係数の周波数軌跡はチャートの定R円(右端に接する円)から外れるとレジスタンスに起伏が発生し、定G円(左端に接する円)から外れるとコンダクタンスに起伏が発生します。R、G両方のグラフにピークが生じるときには、軌跡が定R円からも定G円からも外れる必要があり、最も可能性が高いのは図11に示すように、何らかの理由で反射波の振幅が一律で小さくなった状態が考えられます。図11は理解しやすいように、スミスチャートの外周から大きく減衰させていますが、実際にはほんの少し(1％以下)内側に入るだけで、この傾向が発生します。このような事象の発生する理由としては、以下の可能性が考えられます。
① キャリブレーションの精度が不十分
② 何らかの損失による反射波の減衰(空間への輻射など)

図11　ローカスがスミスチャートの内側にずれたときのイメージ^※4

※4：リアクタンスのピークが2つあるように見えているのはグラフのサンプリング間隔の都合で絶対値にへこみが生じたもので、実際にはピークは1点です。

(4) インダクタは変動要因が多い
インダクタは図6の③に記載されている直流抵抗が6mΩなのに対して、QやSパラメータから導出した値がその25～40倍に達しています。これは巻線の表皮効果による実効抵抗値の上昇とコイルから電磁波が輻射することによる損失の影響が強いことに起因すると考えます。輻射に伴う損失は(3)で述べたようにR、Gの両方にピークが発生する主要因と考えます。大まかな傾向はこれまで述べた通り、何パターンかのモデルで説明できますが、全てを同時に説明できないので、正確な値を必要とする時は実測したSパラメータから導出した値を用いるのが無難と考えます。いずれにせよ、素子のインピーダンスの値に対して1/1000程度の小さな値を測定する必要があり、周辺環境の影響を受けやすいインダクタンスでは特に測定精度が下がりやすいと考えるべきでしょう。

4. 第14話のまとめ

第14話ではデバイスQと共振器のQ、回路の動作Qの関係を説明する予定でしたが、データシート上のQ値とSパラメータの関係をご説明するだけで力尽きてしまいました。元々Qという諸元は精度の悪い値という認識でしたが、ここまでデータシート上の数値が一致しないとは思っていませんでした。

一致しない理由をうまくお伝えするのにどうすれば良いか四苦八苦したつもりですが、今月は非常に読みづらい内容になってしまったのではないかと思います。申し訳ありません。本当は2話で終わる予定でしたが、次回もう一度Qのお話をすることにします。第15話ではSパラメータから導出したQ値を用いて、デバイスQと共振器のQ、回路の動作Qの関係をご説明します。やはり謎の多い諸元“Q”･･･恐るべしです。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年12月号トップへ戻る

【第14話】Qとは何か(その2)

1. キャパシタのQ

2. インダクタのQ

3. Qの精度

4. 第14話のまとめ

NEWS

連載記事

お知らせ

外部リンク