今更聞けない無線と回路設計の話／【テーマ1】三角関数のかけ算と無線工学｜2022年6月号

今更聞けない無線と回路設計の話

【テーマ1】三角関数のかけ算と無線工学
第4話非線形動作を利用したかけ算のまとめ

濱田倫一

第3話では周波数変換回路に求められる機能(乗算式)とこれをアナログ回路で実現する方法について解説しました。通信機で使用されるような周波数変換回路では、帯域幅のある信号(伝送信号)と正弦波(LO信号)を掛け算する必要があり、伝送信号を構成するスペクトル相互は掛け算されないようにする必要がありました。これを実現するためには伝送信号とLO信号との間に大きな振幅差を設け、伝送信号のエンベロープを維持したまま非線形回路を通す必要がありました。第3話では結論だけを先にお伝えしたので消化不良の方も多くおられたのではないかと思います。第4話では掛け算と波形の関係をもう少し掘り下げて解説する事にします。

1. (改めて)足し算された波形と掛け算された波形の違い

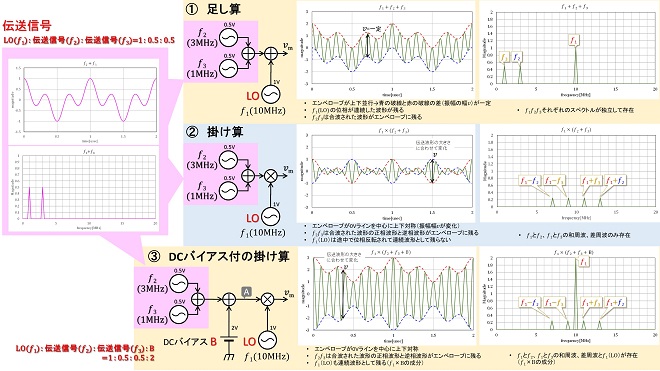
周波数の異なるサイン波を足し算したり掛け算したときにどのような波形になるのかについては、これまで断片的にしか解説できていませんでしたので、改めて図1に纏めました。ここでは第3話に引き続き、LO信号: 𝑓₁(10MHz)と、伝送信号: 𝑓₂(3MHz)+𝑓₃(1MHz)の演算を例に話を進めます。伝送信号の波形を図1の左側、ピンクの吹き出し部分に示します。LO信号との振幅比(LO(𝑓₁) : 伝送信号(𝑓₂) : 伝送信号(𝑓₃)）は1 : 0.5 : 0.5です。吹き出しの中の上側のグラフが時間応答波形(オシロスコープで観測した波形）、下側が周波数スペクトル(スペアナで観測した波形)です。

またLO信号との演算結果を図の右半分に示します。演算は①足し算、②掛け算、③DCバイアス付の掛け算の3種類で、それぞれ左のグラフが時間応答波形、右のグラフが周波数スペクトルです。これらはMicrosoft Excel^※4で計算した結果です。

図1 サイン波の足し算・掛け算による波形の変化^※1

(1) 足し算の波形
図1の①が伝送信号とLO信号(10MHz)を足し算した波形𝑣_mです。計算式で書くと、

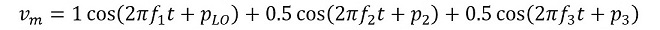
(式1-1)

但し、
𝑓₁: LO信号の周波数(10MHz)、𝑓₂: 伝送信号(𝑓₂)の周波数(1MHz)、𝑓₃: 伝送信号(𝑓₃)の周波数(3MHz)
𝑝_LO: LO信号(10MHz)の位相^※、𝑝₂: 伝送信号(𝑓₂)(1MHz)の位相^※、𝑝₃: 伝送信号(𝑓₃)(3MHz)の位相^※
※図1では𝑝_LO、𝑝₂、𝑝₃は全て0[rad]で計算しています。

ベース注入型のトランジスタミキサにおいては、ベース端子に伝送信号とLO信号を一緒に入力しますが、この時のベース端子の波形に相当します。

伝送信号とLO信号を単純に足し算(合成)すると、合算された時間応答波形は、LO信号の振幅𝑣が伝送信号の波形に沿って上昇/下降する波形となり、伝送信号の波形が合成波形のエンベロープに現れますが、このエンベロープが、LO信号の振幅𝑣の＋側と－側で同じ波形になるのが足し算波形の特徴です。

つまり波形の瞬時値は伝送信号の電圧波形に沿って上下するものの、LO信号の振幅𝑣は常に一定で全てのサイン波が単純に共存している状態です。従って右側の周波数応答波形も1MHz,3MHz,10MHzのスペクトルが単純に並んでいます。

(2) 掛け算の波形
図1の②が伝送信号とLO信号(10MHz)を掛け算した波形です。計算式で書くと、

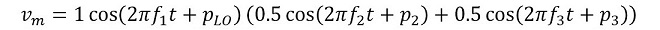
(式1-2)

となり、第2話で解説した理想的な掛け算に該当します。計算式に登場する各変数は(式1-1)と同じです。

伝送信号とLO信号を理想乗算(掛け算)すると、乗算された時間応答波形は、LO信号の振幅𝑣が伝送信号の波形に従って増減する波形となり、伝送信号の電圧が正電圧(＋)のときと負電圧(－)の時で位相が反転します。①と同様、伝送信号の波形が合成波形のエンベロープに現れますが、①と異なり、0Vラインを中心に上下対称になり、－側は位相が反転するのが掛け算波形の特徴です。

つまり、LO信号成分(𝑓₁)は伝送信号と掛け算され、一定周期で位相反転するので、時間軸上でフーリエ積分すると相殺してしまい、周波数軸上では観測されません。同様に伝送信号(𝑓₂+𝑓₃)のエンベロープも＋側と－側に逆相関係で存在するため、時間軸上でフーリエ積分すると相殺して周波数軸上では観測されません。結果、時間軸上で見えているのは第1話で解説した「ビート(うなり)波形」のみです。従って、周波数スペクトルとして観測されるのは図1②の右側のグラフに示すとおり、LO信号と伝送信号の和周波成分と差周波成分のみとなります。

(3) バイアスされた伝送信号との掛け算の波形
図1の③も伝送信号とLO信号(10MHz)の掛け算した波形ですが、系統図に示すように伝送信号にDC(直流)バイアス(図1では+2V)を付加しています。これを計算式で書くと、

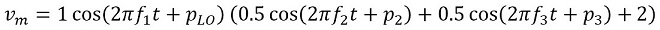
(式1-3)

となります。(式1-2)と同様、計算式に登場する各変数は(式1-1)と同じです。

「なんだこれ?」と思われた方もおられると思いますが、第3話で解説した非線形増幅で等価的に掛け算する方法を用いた場合が最終的にこの演算に該当します。

伝送信号にDCバイアスを加えると図のA点において電圧がマイナスになりません。この信号とLO信号を理想乗算(掛け算)すると、乗算された時間応答波形は②と同様、LO信号の振幅𝑣が伝送信号の波形に従って増減する波形となりますが、②のように(＋)側のエンベロープと(－)側のエンベロープが交差しないので位相が連続しています。エンベロープに現れる伝送信号波形は②と同様、0Vラインを中心に上下対称になり、－側は位相が反転します。(2)と少し形が違いますが、この波形も時間経過で振幅に強弱が発生する「ビート(うなり)」波形です。

つまり、LO信号成分(𝑓₁)は伝送信号と掛け算されてもDCバイアスのおかげで位相反転が起きないので、時間軸上でフーリエ積分しても相殺せず、周波数軸上に𝑓₁のスペクトルとして観測されます。一方、伝送信号(𝑓₂+𝑓₃)のエンベロープは②と同様、＋側と－側に逆相関係で存在するため、時間軸上でフーリエ積分すると相殺して周波数軸上では観測されません。結果、周波数スペクトルとして観測されるのは図1③の右側のグラフに示すとおり、LO信号、ならびにLO信号と伝送信号の和周波成分と差周波成分となります。

2. 極端な非線形回路: ダイオードスイッチ(半波整流回路)

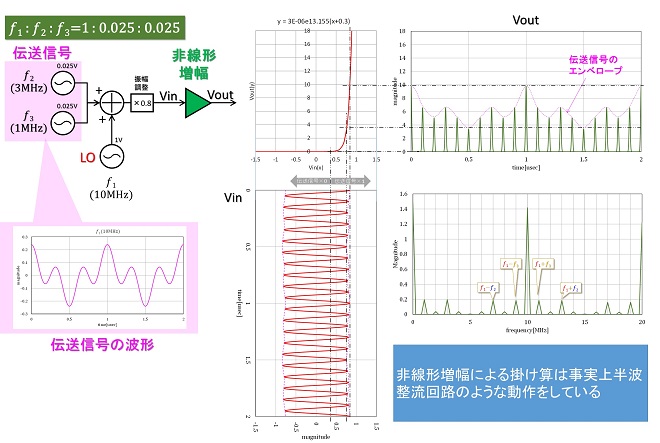
図1の③が第2話～第3話で解説した非線形増幅を用いた掛け算と、どのように対応しているのでしょうか。図2は第3話の図5の再掲ですが、Voutは、Vinの＋の領域のみ増幅された波形であることが解ります。つまり半波整流された波形と概ね同じです。第3話の図5では 𝑓₁×(𝑓₂+𝑓₃)の演算を行うためには、伝送信号のエンベロープが変形しない(歪(ひず)まない)ようにする必要があると解説しました。図2において出力波形のエンベロープに現れる伝送信号の波形を歪ませないためにミキサ回路に要求される理想的な非線形特性とは指数関数ではなく、入力信号が負(－)電圧のサイクルではOFF状態で、正(＋)電圧のサイクルのみ線形増幅する特性･･･所謂半波整流の特性であり、正(＋)電圧のサイクルでは直線増幅してくれる増幅器(回路)が理想だといえます。

図2 非線形増幅を用いた掛け算(第3話図5の再掲)

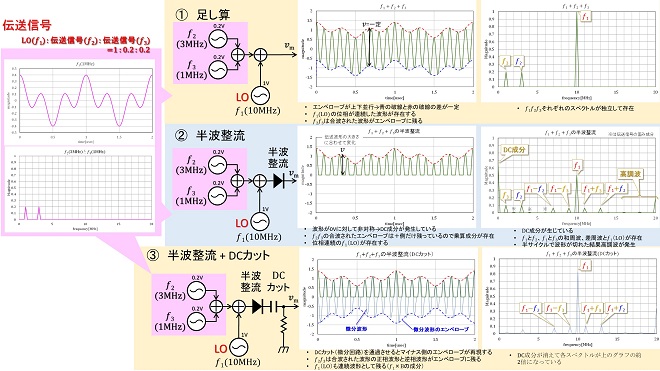
そこで、図1の①で示した足し算波形を単純に半波整流したらどうなるかを図3に纏めました。なお本図に登場するダイオードは理想ダイオード(V_F=0V)です。

図3の①は図1の①と同じく伝送信号(3MHz+1MHz)とLO信号(10MHz)を足し算した波形です。振幅比は図1と同じにするとエンベロープの最低電圧が0Vに達してしまい、半波整流すると丸め誤差分で微妙に波形が歪(ひず)むので、少し伝送信号を小さくして(LO(𝑓₁) : 伝送信号(𝑓₂) : 伝送信号(𝑓₃))は1 : 0.2 : 0.2としています。

図3 半波整流回路による掛け算^※2

(1) 合成波を半波整流したらどうなるか
結果は図3の②に示す通りです。まず②の左側のグラフ(時間応答波形)を見ると、波形の負(－)側がなくなることで、今まで一定だったLO信号の振幅𝑣が伝送信号の振幅に併せて増減するようになります。つまりLO信号に伝送信号と掛け算した成分(ビート波形)が現れるのです。これは伝送信号に対して、LO信号が(－)電圧の期間に0を掛け算している事と等価です。

この演算ではLO信号成分の位相は連続しているのでフーリエ積分しても相殺せず、②の右側のグラフ(周波数応答波形)には伝送信号とLO信号の和周波成分と差周波成分に加えて、LO信号のスペクトルが出現しています。また②の左側のグラフ(時間応答波形)において、エンベロープに現れる伝送信号波形も負(－)側がなくなった事で、フーリエ積分しても相殺されません。この結果、右側グラフ(周波数応答波形)には伝送信号の成分(3MHzと1MHz)も出現しています。

さらに②の右側グラフ(周波数応答波形)には直流成分(0Hz)が現れています。交流信号(サイン波)は時間軸上で積分すると0になります。これはサイン波が0Vを中心に時間軸に対して対称だからです。この特性は周波数の異なるサイン波を複数足し併せても同じです。これに対して②の左側のグラフ(時間応答波形)では、半波整流された電圧波形は振幅が＋側のみに偏っています。従ってこの波形を時間軸上で積分しても0にはなりません。周波数軸上で直流成分が発生するのはこのためです。

また、②の右側グラフ(周波数応答波形)をよく見ると、2MHz、4MHzにも小さなスペクトルが存在します。(※印の部分)これは伝送信号を構成する𝑓₂と𝑓₃が掛け算された成分で、伝送波形がわずかに歪んでいることを示しています。これは半波整流が理想乗算と違い、足し算波形を時間軸で0Vを境にして「ちょん切った」結果、10MHzのデューティー比が微妙に変化している事が原因です。

(2) 半波整流波形がバイアスされた伝送信号とLOの掛け算と等価になる理由
1章の(3)項で、図1の③が第3話で解説した非線形増幅で等価的に掛け算する方法を用いた場合が最終的にこの演算に該当すると申し上げました。つまり、図1の③と図3の②が最終的に同じになります。図3の②にはDC成分が存在するため、時間領域では(＋)の半波成分の波形として観測されました。ここからDC分を除去すると、時間領域波形は0Vを中心に上下対称の波形に変化します(積分したら0になる)。

DC分を除去するとは、コンデンサでDCカットすると言うことです。コンデンサを回路に直列に挿入するので、出力信号は時間領域では微分応答波形として観測される事になります。DCカットをExcelで模擬した結果を図3の③に示します。図3の③の左側(時間領域)のグラフにおいて、緑のプロットは半波整流の出力波形、青のプロットは、緑の波形を適当な時間で微分(表計算なので差分演算で代用)したものです。「適当な時間」としてLO信号の1/4サイクル程度の時間を選択しています。青のプロットは微分応答波形なので、緑の波形が電圧上昇しているところでは(＋)の電圧、電圧垂下しているところでは(－)の電圧になっています。差分演算の時間(微分回路の時定数に相当)を適当に選択することで、緑のプロットに対して約90°の位相進みで、(－)側の振幅が復元された波形になっていることがお解り頂けると思います。この波形は図1の③と概ね等価です。

図3の③右側の周波数領域のグラフを見ると、②に存在していた直流成分がなくなっていることがお解り頂けると思います。この計算では微分回路のハイパス特性が見えてしまい、全体的に右肩上がりの周波数特性がついてしまいました。(－)側が復元されて電圧振幅が2倍になっているので、スペクトルの大きさは図3の②の約2倍になっています。なお電圧が2倍になるのは振幅(電圧)のみの計算、すなわち出力インピーダンスが高い場合の話です。微分回路で電力は増幅されないので、実際の回路では振幅は小さくなります。

これはB級やC級の電力増幅回路において半波しか増幅しないのに、ちゃんと360°位相が連続した高周波出力波形が得られるのと同じ理屈です。実際にはバンドパスフィルタ(共振回路と書かれた教科書もあります)も併用して高調波成分などが含まれない出力波形を抽出します。

3. 伝送信号を構成するスペクトル同士が掛け算されない条件

ここまで書けば、直感的にご理解頂けるのではないかと思いますが、図1、図3において伝送信号を構成する周波数𝑓₂のスペクトルと𝑓₃のスペクトルが掛け算されない為には、伝送信号のエンベロープを歪(ひず)ませない事が条件です。

図1の②③は伝送信号が全く掛け算されない理想条件ですが、何れも𝑣_mのエンベロープに伝送信号波形が歪(ひず)まずに保存されています。「伝送信号を構成するスペクトルが相互に掛け算される」とは、この𝑣_mのエンベロープに現れる伝送信号波形が歪むことと同意です。

第3話で解説した非線形増幅回路の場合、入出力応答特性が指数関数だったので、伝送信号の振幅が指数関数を直線と見なせる程度まで小さくしないと、多かれ少なかれ必ず歪みます。これに対してダイオードを用いた半波整流回路の場合は入力電圧が(－)の時にOFF、(＋)の時にONであり、ON領域では波形は歪みません。従って帯域幅を有する伝送信号とサイン波であるLO信号の掛け算という用途には非線形増幅回路よりも適しているといえます。ダイオードスイッチの場合も、エンベロープを歪ませないためには、LOの振幅＞伝送信号の振幅であることが必要です。理想ダイオードの場合はLOの振幅≒伝送信号の振幅まで無歪みの特性を得る事ができますが、実際のダイオードはターンON電圧付近に強い非線形性が生じるので、エンベロープがこの部分にかからないようにするためには、やはりLOの振幅＞伝送信号の振幅である必要があります。別の見方で言うと、ダイオードのスイッチングはLO信号のみで行う必要があると言うことになります。

4．第4話のまとめ

第4話では代表的なサイン波の掛け算式と、それに対応する時間領域波形、周波数スペクトルの関係を解説しました。いままで曖昧にしていた箇所なので、少しすっきりされたのではないかと思います。また半波整流による掛け算についてもご紹介しました。無線の教科書では、トランジスタミキサによる掛け算は「トランジスタ増幅器の非線形特性を利用して周波数の変換を行う」とさらりと書いてあることが多いのですが、実際には伝送信号のエンベロープに対して線形性を確保する必要があり、B-E間のスイッチング特性(これも非線形特性ではあります)を使用して半波整流しているというのが、より実体に近いと思います。以下、要点を整理します。

① 複数のサイン波を足し算したときの波形は、そのエンベロープが(＋)側と(－)側で同じ形になる。(伝送信号の波形に合わせて信号の電圧は変化するが、振幅は変化しない)
② 複数のサイン波を掛け算したときの波形は、そのエンベロープが(＋)側と(－)側で、位相反転する。(伝送信号の波形に合わせて波形の振幅が変化する)
③ 伝送信号とLO信号を合成(足し算)した後、半波整流された波形も伝送信号の波形に合わせて振幅が変化しているので、両者の掛け算成分が含まれる。半波整流はLO信号の半サイクル毎に0を掛け算しているのと等価である。
④ ③の波形にはDC成分が含まれており、コンデンサによりDCカットを行うと(＋)(－)対称な波形が現れる。
⑤ 伝送信号とLO信号の掛け算において、エンベロープが0Vを跨がないようにバイアスを加えると、乗算の出力にLO成分が現れる。③の波形はこの演算と等価である。
⑥ 伝送信号を構成するスペクトル(周波数の異なるサイン波)同士を掛け算させないためには、掛け算後の波形のエンベロープに現れる伝送信号波形を歪(ひず)ませないようにする必要がある。
⑦ 半波整流回路でこれを実現するためには、ダイオードのスイッチングをLO信号のみで行うように伝送信号とLO信号のレベル差を管理する必要がある。

なお第4話で解説した波形の特徴は周波数変換回路のように離れた周波数の信号同士を掛け算した場合の見え方です。同一周波数の信号を掛け算したり、近い周波数の信号同士を掛け算したりすると、(よく見ると同じなのですが)少し違った感じで観測されます。

今回は回路シミュレータを使用してトランジスタミキサのダイナミックレンジを見るところまでお話ししようと思っていましたが、時間領域波形と周波数領域波形の対応をご説明するだけで力尽きてしまいました。次回はシミュレータを使って⑥について詳しく見ていきたいと思います。

※1: 図1の作図に用いたExcel^※4シートはここからダウンロード^※3できます。

※2: 図3の作図に用いたExcel^※4シートはここからダウンロード^※3できます。

※3: なおダウンロードされたExcelシートに関するご質問についてはご容赦ください。これらExcelシートの内容に関する知的財産権その他一切の権利は筆者濱田倫一に帰属します。月刊FB NEWS編集部は筆者濱田倫一の許可を得て本件記事を掲載しております。また筆者、ならびに月刊FB NEWS編集部は、これらExcelシートの二次使用に伴う一切の責任を負いませんので、あらかじめご了承ください。

※4: Microsoft、ならびにExcelは米国マイクロソフト社の商標です。

今更聞けない無線と回路設計の話　バックナンバー

2022年6月号トップへ戻る