Mr. Smithとインピーダンスマッチングの話／【第4話】伝送線路と反射係数｜2019年2月号

Mr. Smithとインピーダンスマッチングの話

【第4話】伝送線路と反射係数

濱田倫一

第3話まではインピーダンスマッチングのお話を中心に説明してきました。インピーダンスマッチングとは何か、どうやって設計すればよいか、についてイメージをお持ちいただくことができたのではないかと思います。今月はいったんスミスチャートから離れて伝送線路や反射係数の話題です。第1話でお話しした特性インピーダンスについても改めて触れます。無線の教科書を紐解くと、このあたりからオイラーの式が多数登場し、しかもe^jθのθが時間を示している場合と物理座標（立体角）を示している場合が混在するので（少なくとも筆者は）混乱しがちです。

ここでは電磁波の伝搬と「進行波」「反射波」「定在波」「特性インピーダンス」のイメージを理解してもらうために、極力数式を使わずに物理的に少々乱暴な図を用いて解説を進めます。「その説明は矛盾があるだろう」「厳密には間違っている」的なご指摘があるかもしれませんが何卒ご容赦ください。

1. 電流の進む早さ

電流とは何か。中学校の理科か高校の物理では「電池のプラス極からマイナス極に向かう電気の流れの事で、実際には電子（金属中の自由電子）がマイナス極からプラス極に移動する」と教わったと思います。電子工学の世界では「自由電子」の部分についてもう少し概念を拡張して、「キャリア（自由電子、ホール、イオン等の荷電粒子）の移動に伴う電荷の移動＝電流」と定義しています。ではここで問題です。まずは図1の【問題1】から…

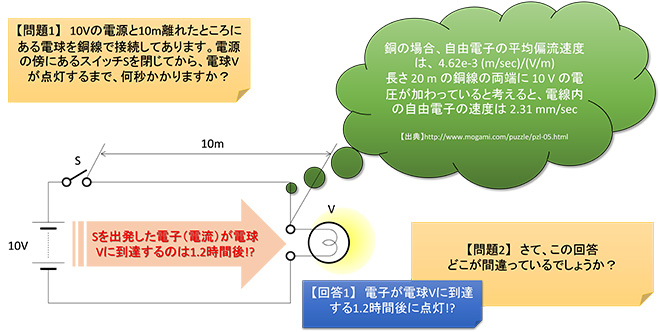
図1　電流の流れる早さはどのくらい？

我々の経験上、スイッチSをONにしたら一瞬で電球Vは点灯するはずです。少し真面目に計算（と言っても概算ですが）してみましょう。

電流の正体は銅線内の自由電子の移動ですから、電流の流れる早さ＝自由電子の移動速度（平均偏流速度=4.62(mm/sec)/(V/m)^※1）と考えると、図1の吹き出しに書いた通り往復20mの銅線の両端に10Vの電圧を印加した^※2ので銅線内の電界強度は10[V]/20[m]＝0.5[V/m]となり、自由電子の移動速度は4.62×0.5=2.31mm/sec、スイッチSから電球Vまで10mですから、スイッチSをONにしてから電球Vが点灯するまでの所要時間は4329sec=1.2hoursとなります。･･･て、そんなわけ無いですよね。何処が間違っているのでしょうか？　→【問題2】

なお回答1で用いた自由電子の偏流速度（電流が流れるメカニズム）についてはインターネットを検索すると沢山解説されているので、そちらを参考にしてください。筆者は右のURLを参考にしました　→　http://www.mogami.com/puzzle/pzl-05.html

それにしても遅いですね。しかも電気信号の伝わる早さが電圧の大きさで変化するというのは経験上あり得ません。実はスイッチSをONにすると一瞬で電球Vが点灯する理由は”銅線に10Vの電圧が加わった”という変化が電磁波として光の速さで電球まで伝わる為です。伝わった先で流れる電流の早さは回答1で計算したとおりです^※3。光の速さは299792458[m/S]（約3×10⁸[m/s]）ですから、スイッチSから10ｍ先の電球Vまでは約33nsecです。この間の様子を図2(a)～(d)に4コマ漫画風に示します。

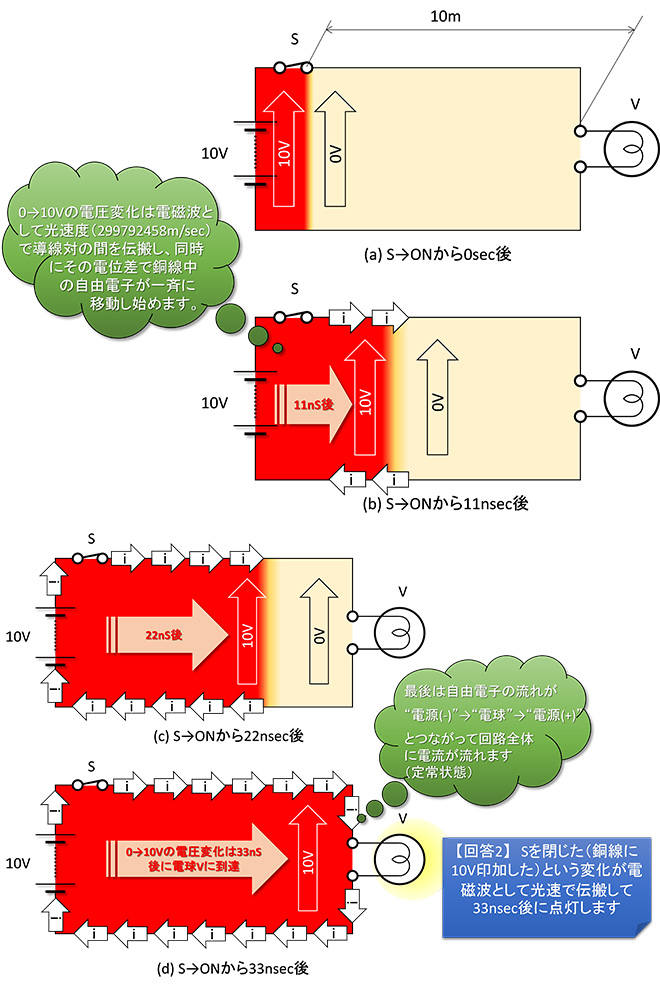
図2　スイッチSをONにしてから電球Vが点灯するまでの出来事

川下にいて上流の水門が開いた瞬間を想像してください。スイッチSをONにすると、＋側と－側の2本の銅線間の電圧はスイッチ側から電球Vに向かって順次0V→10Vに上昇します（図2(a)→(c)）。この電圧の上昇は電磁波によるもので、光の速さで電球Vに向かって伝搬してゆきます。銅線内では電圧が上昇した区間から（電界強度が上昇するので）順次自由電子が移動し始めます（＝電流が流れ始める：図中の）。スイッチSをONにしてから33nsecが経過し、電圧上昇の波が10m先の電球Vまで到達すると、銅線内のすべての区間で電界強度が0.5V/mになるので、銅線内のすべての自由電子が【問題1】で解いた速度で（ゆっくりと）循環し、電球Vに電流が流れて点灯します（定常状態）。

※1この数値も記載のURL（http://www.mogami.com/puzzle/pzl-05.html）から引用しています。
※2話を簡単にするために電球の存在を無視しています。
※3電圧のかかり方が10V/20mではなく、もっと微視的な区間になるので厳密にはもっと早くな
るはずです。

2．最初は何アンペア？

電流の流れる速さは極めて遅いと言うことと、我々が常識として理解している電気が伝わる早さは実は電磁波の伝搬によるものだったということについてご理解いただけましたでしょうか。引き続き、電気が伝わり始めるときの電流と電圧の動きについて考察してみましょう。ここからは図2の(d)を図3に置き換えて考えてみます。

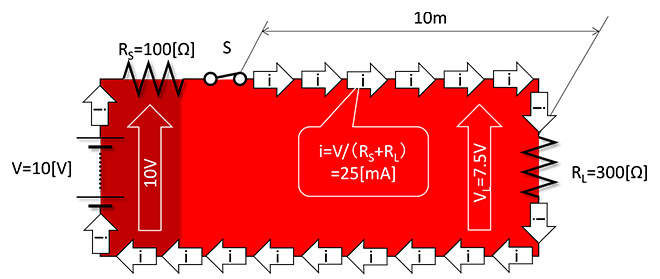
図3　iの大きさは？（その1）

1章では電流の流れる早さにフォーカスしましたので回路の電圧・電流は大雑把な書き方をしました。図3では電圧・電流の大きさを考えてみたいので、電球Vに替えて負荷抵抗RL（300Ω）を接続しました。また説明の都合で恐縮ですが、後々の話がややこしくならないように電源インピーダンス（抵抗）RS（100Ω）を定義（挿入）しました^※4。図3の回路の定常状態での電圧と電流の関係を求めるのは簡単ですね。
回路電流iの大きさは $i = \frac{V}{R_{S} + R_{L}} = \frac{10 [V]}{100 [Ω] + 300 [Ω]} = 25 [mA]$ 　（式2-1）
負荷抵抗の端子電圧VLは $V_{L} = i \times R_{L} = 25 [mA] \times 300 [Ω] = 7.5 [V]$ 　（式2-2）

です。では図4に示すようにスイッチSをONにしてから電磁波が負荷抵抗RLに到達するまでの時間33nsec以内に流れる電流の大きさは一体何アンペアなのでしょうか。なにしろスイッチSを出発した電磁波はまだ10m先の負荷抵抗RLまで到達していません。

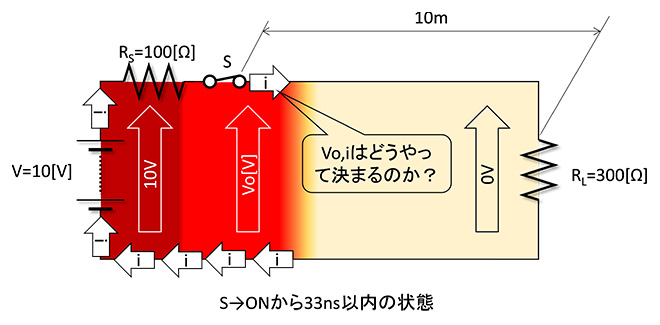
図4　iの大きさは？（その2）

3．再び特性インピーダンス

実はスイッチSをONにしてから電磁波が負荷抵抗RLに到達するまでの間に流れる電流の大きさは、その配線の特性インピーダンスZoで決まります。第一話でも登場しましたが、図5に示すように特性インピーダンスとは配線に分布する単位長あたりのインダクタンスとキャパシタンス（図4で云うとスイッチSから負荷抵抗RLまでを結ぶ＋／－の2本の銅線の単位長あたりのインダクタンスと銅線間に分布する単位長あたりのキャパシタンス）の比の平方根で決まる値です。

配線に分布するインダクタンスとキャパシタンスはその配線の断面形状（＋の線と－の線の位置関係と形状、ならびにその間の絶縁物の材料と形）で決まります。従って電源から負荷までの全経路で特性インピーダンスを一定の値にするためには、配線の断面形状をずっと同じにする必要があります。このことに配慮して作られた配線経路を「線路」と呼び、最も身近にあるのは、Zo＝50Ωや75Ωの同軸ケーブルや、Zo=300Ωの平行フィーダーなどです。

図5に同軸ケーブルの特性インピーダンスの算出方法を示します。

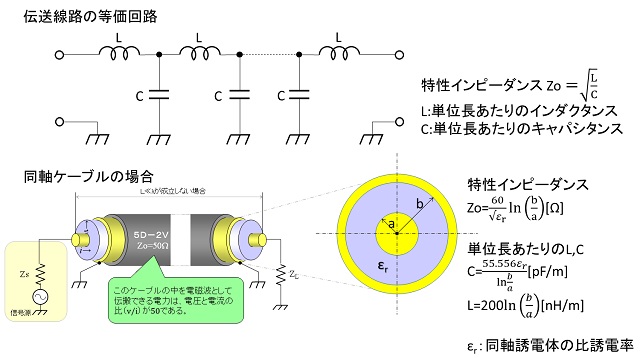
図5　特性インピーダンスとは

今仮に図4のスイッチSから負荷抵抗RLまでの特性インピーダンスZoが100Ωだったとすると、（平行2線の特性インピーダンスは概ね100～300Ωになります）図6に示すスイッチSをONにしてから電磁波が負荷抵抗RLに到達するまでの33nsecの間、
電磁波が到達したところの線間電圧VOと電流iの関係は $i = \frac{V_{O}}{Z_{O}}$ 　（式3-1）
線間電圧VOは電源インピーダンスRSと特性インピーダンスZOでVを分圧することになるので
$V_{O} = \frac{V ∙ Z_{O}}{R_{S} + Z_{O}} = \frac{10 [V] \times 100 [Ω]}{100 [Ω] + 100 [Ω]} = 5 [V]$ 　（式3-2）
従って
$i = \frac{5 [V]}{100 [Ω]} = 50 [mA]$ 　（式3-3）
となります。つまり回路に電圧を印加して最初は負荷抵抗RLの値と関係なく、電源インピーダンスRSと特性インピーダンスZOで決まる大きさの（図6では5V・50mA）電磁波が負荷抵抗RLに向かって進んで行く事になります。

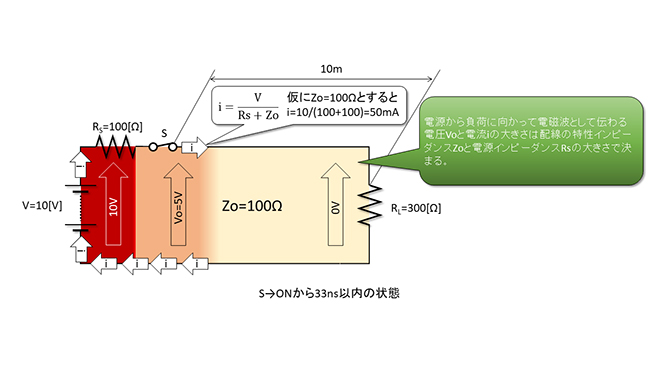
図6　電圧を加えた一番最初の線間電圧と回路電流はZoで決まる

※4　多重反射の説明を避ける為、電源インピーダンスと特性インピーダンスは整合状態としました。

4．進行波と反射波と電圧反射係数Γ

ここまで説明して「あれ？」と思った方は大勢おられると思います。この回路の負荷抵抗RLは300Ωなので定常状態では図3に示したとおりVL = 7.5Vでi = 25ｍAだった筈です。なのにスイッチSをONにしたとたん、この回路の線間を負荷に向かって進む電圧・電流は5V・50mAだと申し上げたのですから･･･。

図6の状態がこの後どうなるのかを示したのが図7の(a)～(c)になります。すなわち電源Vから負荷RLに向かって進行してきた5V・50ｍAの電磁波は、スイッチSをONにしてから33nsec後に負荷抵抗RLに達します。図7(a-1)に示す通り、この電磁波の0.25Wの電力を300Ωの負荷抵抗Rですべて消費しようとするとVL=8.7Vの端子電圧が必要ですが、端子電圧は5Vしかありません。
従って5[V]²/300[Ω]=83[mW]は負荷抵抗RLで消費されますが、残りの167mWは行き場を失うことになります。海岸で防波堤にぶつかった波を想像してください。この結果、負荷抵抗RLの端子間では図7(a-2)に示すように、以下の事が同時に起こります。

①余剰の電力でRLの端子電圧VLがVOからVO＋Vrに上昇する。
②RLの端子電圧VLの上昇に伴い、RLに流れる電流iLは $i_{L} = \frac{V_{L}}{R_{L}} = \frac{V_{O} + V_{r}}{R_{L}}$ となって増加する。
③同時にVO < VLとなるので、負荷抵抗RL側から電圧Vr、電流irの電磁波が電源Vに向かって戻って行く。この時のirの大きさはir = 入射電流i－負荷電流iLとなる。
④電源Vに向かって戻っていく電磁波の大きさは電源から入射した電力（0.25W）からRLが消費した分を差し引いた値であり、かつ電圧と電流の関係が配線の特性インピーダンスZOに縛られる。

最終的にVOとVrは右の関係になって釣り合う $\frac{V_{r}}{V_{O}} = \frac{R_{L} - Z_{O}}{R_{L} + Z_{O}}$ 　（式4-1）

この電源Vから負荷抵抗RLに向かって進む電圧VL・電流iの電磁波を「進行波」、負荷抵抗RLから電源Vに戻る電圧Vr・電流irの電磁波を「反射波」、そして（式4-1）のVr/VOを電圧反射係数Γと呼びます。図7の場合(a-2)のタイミングで発生した反射波の大きさは
$Γ = \frac{R_{L} - Z_{O}}{R_{L} + Z_{O}} = \frac{300 [Ω] - 100 [Ω]}{300 [Ω] + 100 [Ω]} = 0.5$ 　（式4-2）

$i_{L} = \frac{V_{O} + V_{r}}{R_{L}} = \frac{5 [V] + 2.5 [V]}{300 [Ω]} = 25 [mA]$ 　（式4-3）
から、
$V_{r} = Γ ∙ V_{O} = 0.5 \times 5 [V] = 2.5 [V]$ 　（式4-4）
$i_{r} = - (i - i_{L}) = - (50 [mA] - 25 [mA]) = -25 [mA]$ 　（式4-5）

となります。この反射波が図7(b)→(c)の流れで電源Vまで戻った時点で電源Vから負荷抵抗RLまでの回路全体の電圧、電流が一定値となり定常状態に移行します。図3と図7(c)を比べて見てください。各部の電圧、電流値は同じ値になっています。

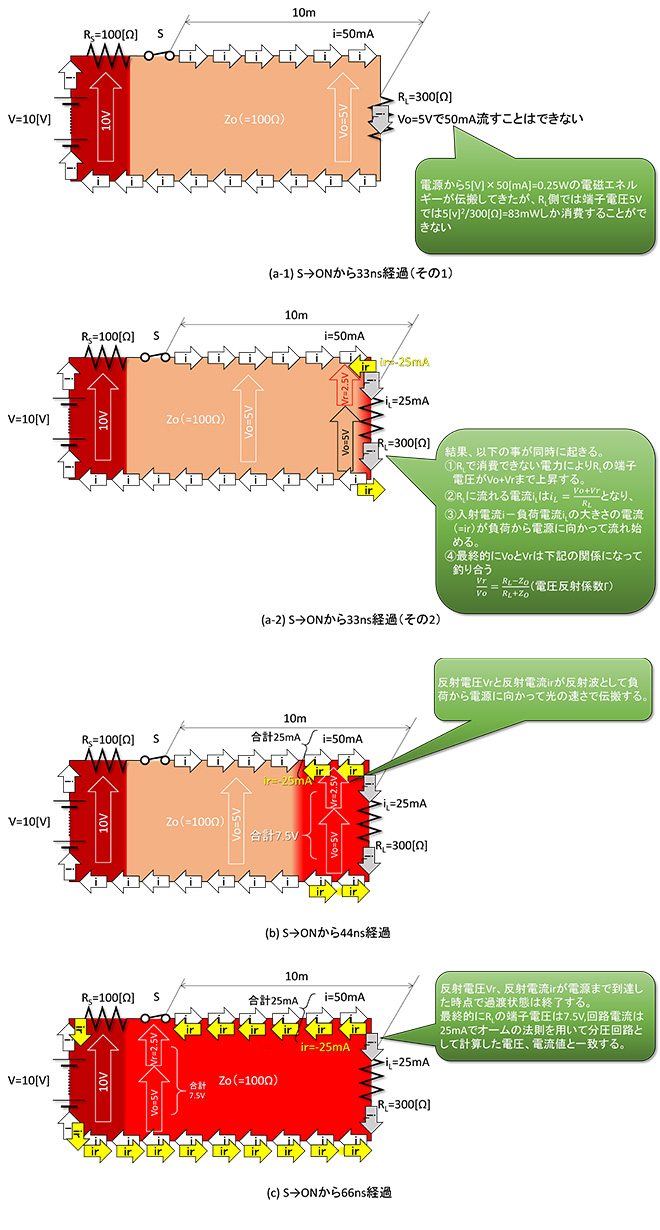
図7　スイッチSをONにしてから定常状態に至るまで

図7では線路の特性インピーダンスZoよりも負荷抵抗Rの値が大きい場合について説明しましたが、特性インピーダンスZoより負荷抵抗RLの値が小さい場合は反射係数Γが負の値となり、反射波の極性が反転します。またZo=RLの時は反射波の大きさは「0」となります。

5．直流と交流の違い

特性インピーダンスとか進行波とか反射波とかのイメージは掴んでいただけたかと思います。ここまでは直流回路で考察してきましたが、交流回路だとどうなるのでしょうか。交流回路の考察を行うために図３の回路を今度はスイッチSを図８のように極性反転回路に組み替えます。そしてこのスイッチを（人間業では無理ですが）約3.3usec毎に切り替え、すなわち150kHzで極性反転させた場合を考えてみます。

スイッチSを＋から－に切り替えた時に発生する進行波・反射波の往復は、直流回路の時と同様です。直流回路との違いは3.3usec毎に繰り返し発生することですが、配線長10mでは電磁波の往復時間は66nsecで3.3usecに対して十分に短く、進行波と反射波は同位相と取り扱ってもほとんど問題になりません^※5。従って直流回路と同じ取り扱いが可能です。ちなみにスイッチ切り替え（＝矩形波）ではなく正弦波の場合は電圧が連続的に変化するので、常に進行波、反射波が発生しているといえますが、スイッチの場合と同様、電磁波の往復時間に対して電圧変化は非常に緩やかですので、やはり直流回路と同じと考えて特性インピーダンスの存在を無視して扱っても実害はありません。

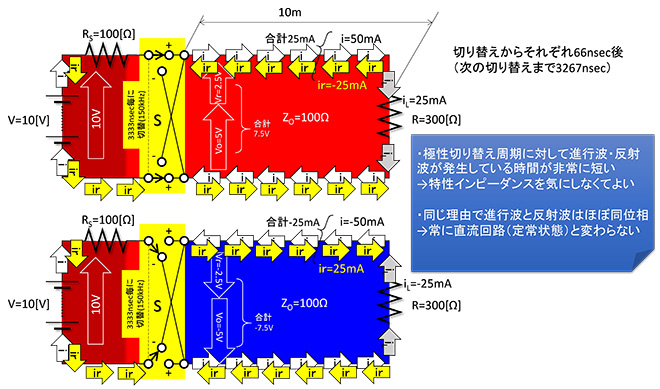
図8　150kHzで極性反転したらどうなるか

では、もっと早く極性反転したらどうなるでしょうか。今度は11ns毎（45MHz）に極性反転した場合の状況を図9に示します。図9の(a)～(b)に示すように電源Vを出発した進行波が負荷抵抗RLに到達するよりも早く電源Vの極性が反転してしまうため、極性の異なる波が次々に発生して負荷抵抗RLに向かって進んでゆく事になります。海で小舟に乗っていて大きな船が近くを通過したときに何度も揺られるようなイメージでしょうか。最初の進行波が負荷抵抗RLに到達すると、負荷抵抗RLの両端では直流パルスの時と同様、電圧反射係数Γで決まる電圧が反射波として電源に向かって戻り始めます（図9(c)～(e)）が、最初の反射波がスイッチSまで戻るよりも早く電源の極性が変化して新たな進行波が発生しているので、特性インピーダンスの影響が定常的に観測される事になります。高周波回路において電源や負荷のインピーダンスと同軸ケーブルの特性インピーダンスを整合させる必要が生じる理由はここにあります。

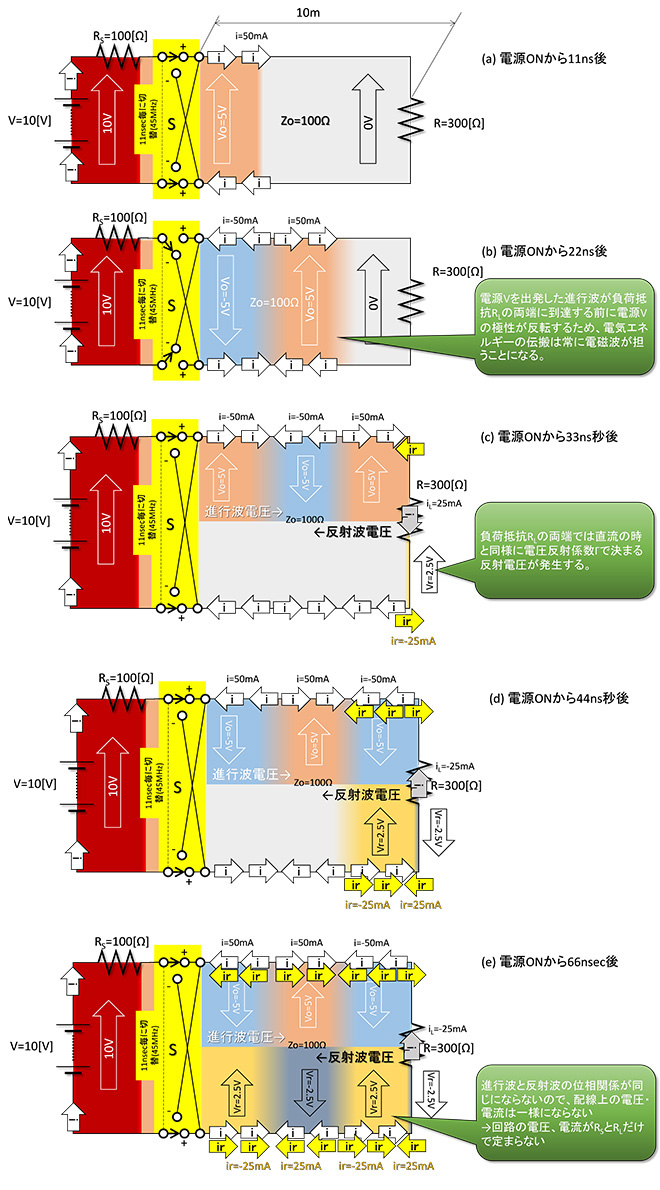
図9　45MHzで極性反転したらどうなるか

※5　厳密には150kHz(λ=2000m)に対して10ｍ(λ/200)の長さを無視できるかは時と場合によります。
150kHz正弦波の伝送であれば無視できることが多いですが、ディジタル信号のように矩形波で波形の立ち上がり／立ち下がりを気にする場合は無視できません。

6．定在波

図7と図9を比較すると図9(d)～(e)は反射波の書き方が変わってることにお気づきと思います。進行波が負荷抵抗RLに到達する前に電源が極性反転するような回路では、同様に反射波が電源に到達するまでに進行波の極性が反転しているので、配線上の電圧（進行波電圧VO＋反射波電圧Vr）は配線上のどの位置で観測するかによって複雑に変化します。このため図9を図7のようにVO+Vrで色分けす表示ると非常にややこしくなったので、上下2分割して進行波と反射波を別々に表記しました。

つまり直流パルスや低周波交流の場合は進行波と反射波の位相が常に同じだったので電磁波による最初の伝搬が終わった後は電源抵抗RSと負荷抵抗RLだけで回路の電流・電圧を考える事ができたのですが、進行波が負荷に到達する前に電源が極性反転してしまうような高い周波数の交流では、進行波と反射波の位相が配線の長さによって揃ったりずれたりしてしまうため、電源抵抗RSと負荷抵抗RLに加えて特性インピーダンスZOと配線（線路）の長さも考慮する必要があります。中学校の理科でロープを使って実験された方もおられると思いますが、進行波と反射波のように進行方向の異なる2つの波が干渉すると、固定的に振幅が大きくなったり小さくなったりする場所が現れ、これを定在波と呼びます。定在波が発生する状況では電源と負荷の間の長さによって、電源から見える負荷インピーダンスの大きさが変化するなどの複雑な現象が発生しますが、このあたりは次回に詳しくご説明します。

7．第4話の内容と波長の関係

第4話では電源と負荷の間の距離が10mの場合を例にとって電流の流れ方をご説明しました。10mの長さを電磁波が往復するには66nsの時間が必要で、それよりも短い周期で電源の極性が反転すると進行波、反射波の振る舞いが定常的に見えるようになる　というのが話の骨子でした。

一般論に置き換えると、交流信号において極性反転が発生するのは1/2サイクル毎ですから電磁波が往復する時間内に1/2サイクル以上振動する場合は進行波、反射波の影響が定常的に見えるということになります。さらに云うとこれは長さがλ/4に該当するので、交流回路において、長さがλ/4以上の配線は特性インピーダンスを意識する必要あり　ということになります。配線の長さがλ/4以下だったら特性インピーダンスは無視してよいかというと、そうではなく実際にはλ/100を超えるあたりから徐々に進行波／反射波の振る舞いが見えて来ます。

8．第4話のまとめ

第4話では電流の流れ方と電磁波の関わりを中心に以下の内容を解説しました。

（1）自由電子などの荷電粒子の移動で流れる電流の早さは非常に遅い。
（2）一方で電圧・電流の変化は電磁波として光の速さで伝搬する。
（3）電磁波が配線（線路）を伝搬する時、配線（線路）上を流れる電流の大きさは負荷抵抗ではなく線路の特性インピーダンスの値で決まる。
（4）電磁波が配線（線路）を伝搬するときは、端子電圧と特性インピーダンスで決まる電力の進行波が電源から負荷に向かって伝搬し、負荷端で特性インピーダンスと負荷インピーダンスの不整合により余剰、または不足となった電力が反射波として負荷から電源に戻る。
（5）配線長が波長に対して十分短ければ、反射波が電源まで戻った時点で、回路の各部の電圧・電流は電源インピーダンス、負荷抵抗インピーダンスと電源電圧からオームの法則で計算した電圧・電流値と同じ結果になる。
（6）電源と負荷の間の長さが波長に対して無視できなくなると電磁波での伝搬が定常的かつ支配的になるため、常に特性インピーダンスを考慮する必要がある。
（7）電磁波による伝搬は反射波の発生が伴うため、配線（線路上）上に定在波が発生する。

今回は進行波、反射波、定在波の振る舞いをすべてご説明しようと思っていたのですが、いざ書き始めると、4コマ漫画を沢山つくった事もあってあまり書き進みませんでした。

次回はスミスチャートと反射係数の関係をご説明しようと考えていましたが、引き続き「定在波」の話を中心にVSWRや反射係数について解説することにします。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年2月号トップへ戻る

【第4話】伝送線路と反射係数

1. 電流の進む早さ

2．最初は何アンペア？

3．再び特性インピーダンス

4．進行波と反射波と電圧反射係数Γ

5．直流と交流の違い

6．定在波

7．第4話の内容と波長の関係

8．第4話のまとめ

NEWS

連載記事

テクニカルコーナー

お知らせ

外部リンク