Mr. Smithとインピーダンスマッチングの話／【第5話】伝送線路と反射係数（その2）｜2019年3月号

Mr. Smithとインピーダンスマッチングの話

【第5話】伝送線路と反射係数（その2）

濱田倫一

第4話では解っているようで解っていない電気エネルギーの伝搬メカニズムを解説し、電圧変化、電流変化は電磁波として配線を伝搬するが故に回路電圧の変化時には「進行波」「反射波」が発生することをご説明しました。第5話では引き続き反射係数と電源インピーダンス、特性インピーダンス、負荷インピーダンスの関係について解説します。

1. 反射係数Γの大きさ

第4話のおさらいになりますが、進行波の電圧・電流は配線（線路）の特性インピーダンスZoで決定され、反射波の電圧・電流は特性インピーダンスZoと負荷インピーダンスZL（第4話ではRLで説明しました）の関係で決定されます。従って進行波電圧と反射波電圧の比である電圧反射係数ΓもこのZoとZLの関係として定義されます。これらの関係を改めて図1にまとめます。

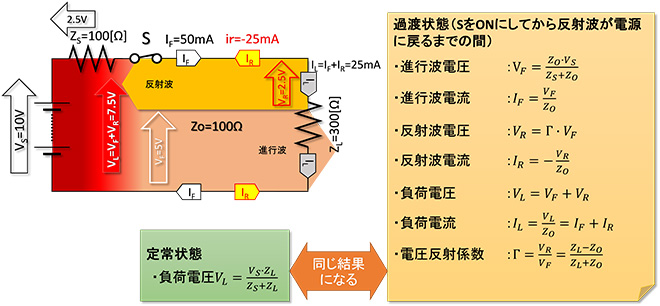
図1　進行波／反射波の振幅とZS,Zo,ZLの関係（第4話の整理）

定常状態の回路電圧・電流は、電源インピーダンスZS、負荷インピーダンスZL、ならびに電源電圧VSの値で決まるのですが、スイッチSを閉じた直後は電源から負荷が見えない状態ですので、進行波の大きさは配線（線路）の特性インピーダンスZoと電源インピーダンスZS、ならびに電源電圧VSで決まります。そして負荷インピーダンスZLからの反射波が負荷端から電源端まで戻ってきて初めて電源から負荷が見える状態、すなわち定常状態になります。では負荷インピーダンスZLを変化させると反射波の大きさはどのように変化するのでしょうか。

（1）直流の場合
負荷抵抗ZL（RL）が取り得る値の範囲は、0Ω（Short）～∞Ω（Open）の範囲になります。ここでは引き続き図1の回路を例にとり、ZL=∞Ω（Open）、ZL＝0Ω（Short）、ZL＝Zoの3つのケースを説明します。

①ZL=∞Ω（Open）
図2に示す通り、終端に電力を消費するものがないので、反射係数Γ=1となり、進行波電圧のすべてが同極性で電源側に反射します。従って配線（線路）上の電圧（＝開放端の電圧）は進行波電圧の2倍、本図では＝VSとなります。一方電流は進行波電流がすべて逆極性で反射されるので相殺されて0ｍAとなります。開放しているのですから当然ですね。

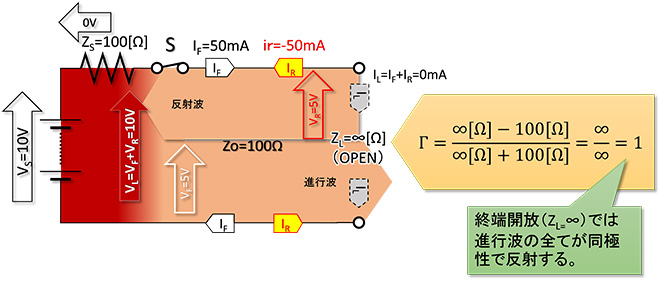
図2　ZL=∞Ω（Open）の場合

②ZL=0Ω（Short）
図3に示す通り、やはり終端に電力を消費するものがないので、進行波のすべてが反射波となりますが、反射係数はΓ=－1となり、逆極性で電源側に反射します。この結果、配線（線路）上の電圧（＝短絡箇所の電圧）は進行波電圧を相殺して0Vとなります。短絡しているのですから直感的にご理解いただけると思います。電流は進行波電流が同極性で反射されるので 2倍の100mA となります^※1。

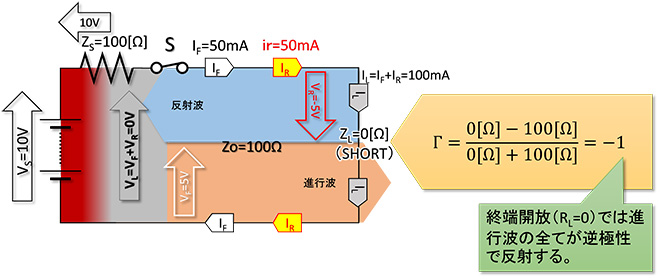
図3　ZL=0Ω（Short）の場合

③ZL=Zo
図4にZS=100Ω（ZL=Zo）の状態を示します。この場合は負荷が進行波の波動エネルギーをすべて消費する（過不足無く消費する）ことができるので、電圧反射係数Γ=0となり、反射波は発生しません。この結果、配線（線路）上の電圧は進行波電圧と同じ5V、電流値も進行波電流と同じ50mAで、いわゆる「整合状態」となります。

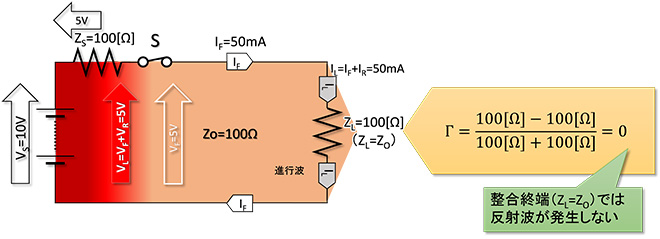
図4　ZL=100Ω（ZL=Zo）の場合

※1　余談ですが、ZL=0Ωの時、もし電源インピーダンスZSが0Ω（線路に定電圧電源を直結した状態）だったらどうなるかというと、最初は10V100mAの進行波がZLまで進みZL端で－10V100mAの反射波になって電源端に戻り、ZoとZSの間でもΓ=－1で今度は反射波が再反射されて進行波に加わり、それが負荷で再度反射されて･･･を繰り返す事になるので、回路の電流値はどんどん上昇してゆき、最終的に∞に達する事になります。これが我々のよく知る短絡状態です。

（2）交流の場合
ここまでは話を簡単にするために直流電源を用い、電磁波が電源から負荷まで1往復する間の事象で説明してきました。ここからは図1の回路の直流電源を交流電源に変更して説明します。電源インピーダンスZS、配線（線路）の特性インピーダンスZo、電源電圧VS（最大値）の値は図1と同じです。回路が交流になると、ZLの取り得る値の範囲にリアクタンス成分（jX）が加わります。また極性が時間とともに反転するので配線（線路）長も考慮しなければならないのですが、ここでは配線の長さが無視できる（電磁波が電源から負荷まで伝搬して負荷で反射して電源に戻ってきても電圧がほとんど変化していない）程度に低い周波数だとして考察します。

①ZLが純抵抗（jX=0Ω）の場合
この場合、配線の長さが無視できる範囲においては電源が直流の場合と同じ結果になります。周波数が高くなって、電源に反射波が戻ってくる前に電源電圧が大きく変化するケースは後ほど解説します。

②ZLが誘導性リアクタンス（ZL=+jX）の場合
図5にZL=j100Ωのインダクタを接続した場合を示します。この時電圧反射係数Γは

$Γ = \frac{Z_{L} - Z_{O}}{Z_{L} + Z_{O}} = \frac{j100 [Ω] - 100 [Ω]}{j100 [Ω] + 100 [Ω]}$

→分母、分子を100で割って $= \frac{(- 1 + j 1) [Ω]}{(1 + j 1) [Ω]}$

→分母分子に1-j1を掛ける $= \frac{(- 1 + j 1) (1 - j 1)}{(1 + j 1) (1 - j 1)} = \frac{j 2}{2} = j 1$ 　　（式1-1）

となって進行波電圧に対して反射波電圧の位相が90°進みます。この結果負荷電圧VLは5+j5[V]、負荷電流ILは50-j50[mA]となります。スイッチSを閉じた直後、電源インピーダンスZS両端の電圧はIF×ZS=50[mA]×100[Ω]=5[V]となり、その後反射波が戻ってきた時点で、反射電流IRが加算されて、(IF+IR)×ZS=(50-j50)[mA]×100[Ω]=5-j5[V]となります。

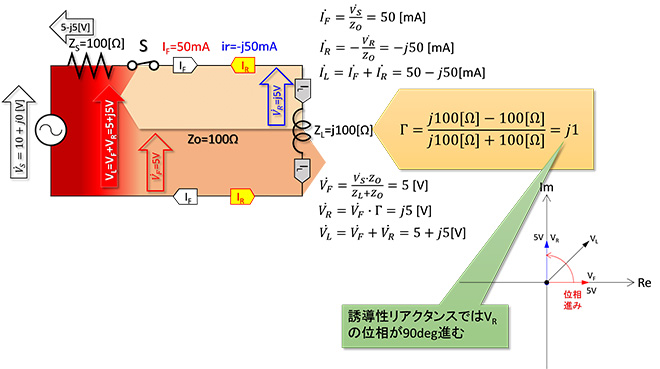
図5　ZL=j100Ω（inductive）の場合

③ZLが容量性リアクタンス（ZL=-jX）の場合
図6にZL=-j100Ωのキャパシタを接続した場合を示します。この時電圧反射係数Γは

$Γ = \frac{Z_{L} - Z_{O}}{Z_{L} + Z_{O}} = \frac{- j 100 [Ω] - 100 [Ω]}{- j 100 [Ω] + 100 [Ω]} = \frac{- j 2}{2} = - j 1$ 　　（式1-2）

となって進行波電圧に対して反射波電圧の位相が90°遅れます。この結果負荷電圧VLは5-j5[V]、負荷電流ILは50+j50[mA]となります。スイッチSを閉じた直後、電源インピーダンスZS両端の電圧はIF×ZS=50[mA]×100[Ω]=5[V]となり、その後反射波が戻ってきた時点で、反射電流IRが加算されて、(IF+IR)×ZS=(50-j50)[mA]×100[Ω]=5-j5[V]となります。

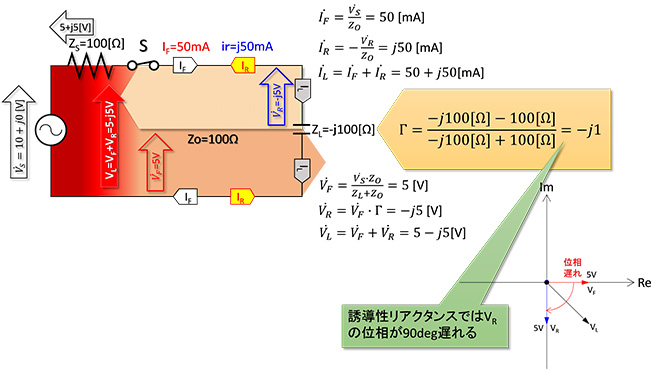
図6　ZL=-j100Ω（capacitive）の場合

（3）反射係数Γの取り得る値の範囲（Γ平面）
（1）（2）で負荷インピーダンスZLと電圧反射係数Γの関係を説明しましたが、これを図にすると図7に示す通りとなります。繰り返しの説明になりますが反射波の源は負荷インピーダンスZLで消費されなかった進行波電力の残りなので、その絶対値が進行波の大きさを超えることはありません。従って電圧反射係数Γの最大値は｜Γ｜≦1となります。そしてZLが実数値（すなわち抵抗成分のみ）の場合は実軸上に存在し、左端が0Ω、中心がZoΩ、そして右端が∞Ωとなります。ZLが複素インピーダンスの場合はΓも複素数となりますが、ZLの虚部が誘導性リアクタンスの場合は上半分、容量性リアクタンスの場合は下半分の領域となります。

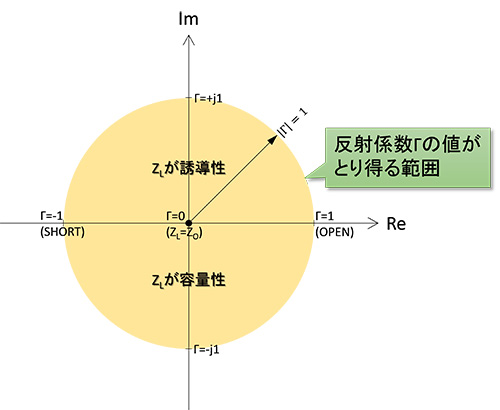
図7　Γ平面

2. スミスチャートの正体

ここまで説明すると、察しの良い方はお気づきの事と思います。左端が0Ω、中心がZoΩ、そして右端が∞Ω。上半分が誘導性で下半分が容量性･･･　第3話の図2を思い出してください。

スミスチャートというのは、このΓ平面に対応する負荷インピーダンスの値をプロットしたものなのです →図8 。電圧反射係数Γは線路の特性インピーダンスZoと負荷インピーダンスZLの相対的な関係で決まるため、スミスチャートのインピーダンス目盛はすべてZoで正規化された値をとる事になるのです。従って第四話から第五話の図6までの回路に適用する場合、スミスチャートの中心は50Ωではなく100Ωと云うことになります。

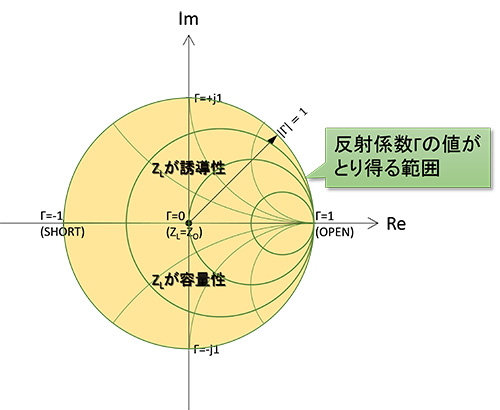
図8　図7にインピーダンスの目盛を書いてみる･･･

このことは言い換えると、電圧反射係数Γと負荷インピーダンスZLは1対1で対応しており、ある2端子回路に信号源インピーダンスZoの電源を接続して電圧反射係数をベクトル測定すれば、その2端子回路のインピーダンスはスミスチャートを用いて一意的に求める事ができると云うことです。実はスミスチャートの本来の用途はインピーダンス、アドミッタンスの合成計算ではなく、伝送線路や給電線路において反射係数からインピーダンスを求めるために考案された図なのです。

3. 高周波回路のオカルト現象

電源から負荷を見た時の反射係数が、負荷のインピーダンスを表していることはご理解いただけたかと思います。では第四話の時のように電源から負荷までの距離が10mあって、周波数が45MHzの電源を接続した場合を考えてみましょう。図9は第4話の図9を正弦波電源に書き換えたものです。45MHzの交流電圧は波長6.6m、電源から負荷まで10m離れると、電磁波が電源を出発して負荷に到達する前に電源の極性が変化してしまいます。つまり、ある瞬間の配線上（線路上）の電圧を観測すると、電源（図ではA点）から負荷までの位置によって異なる電圧が観測されることになります。反射波に対しても同じ事がおこり、負荷（反射点）から電源に到達するまでに反射波の極性が反転するので、負荷から電源までの位置によってある瞬間の反射波の電圧は異なる値になります^※2。この時、電圧反射係数Γはどのようになるのでしょうか。

（1）負荷インピーダンスZLの両端の反射係数
配線上の任意の場所の電圧反射係数Γは、その場所のある瞬間の進行波電圧と反射波電圧の比になります。負荷インピーダンスZL両端の電圧反射係数ΓL（厳密にはZLから負荷側を見たときの電圧反射係数）はこれまで説明した通り（式3－1）で示す値となります。

$Γ_{L} = \frac{V_{R(@ZL)}}{V_{F(@ZL)}} = \frac{Z_{L} - Z_{O}}{Z_{L} + Z_{O}}$ 　　（式3－1）

（2）電源の両端の反射係数
次にZLの10m手前にある電源（図9のA点）から負荷側を見たときの電圧反射係数ΓAはどうなるでしょうか。A点においては、進行波に対して反射波が負荷までの往復20m分に相当する位相遅れを生じるため、（式3－1）に位相回転の項が追加されて（式3－2）で示す値となります。

$Γ_{A} = \frac{V_{R(@A)}}{V_{F(@A)}} = Γ_{L} e^{-jβ×20[m]} = \frac{Z_{L} - Z_{O}}{Z_{L} + Z_{O}} e^{-jβ×20[m]}$ 　　（式3－2）

ここでβは「位相定数」と呼ばれる値で、電磁波が線路上を進む際に、単位長さあたり何[rad]の位相回転が生じるかを示します。→（式3－4）
線路上の任意の場所から負荷側を見たときの電圧反射係数Γは、その場所から負荷までの距離（電気長）をL[m]、負荷端の電圧反射係数をΓLとすると、（式3－3）で表されます。

$Γ = \frac{V_{R(@A)}}{V_{F(@A)}} = Γ_{L} e^{-jβ2L} = \frac{Z_{L} - Z_{O}}{Z_{L} + Z_{O}} e^{-jβ2L}$ 　　（式3－3）

β：位相定数= $\frac{2 π}{λ} [rad⁄m]$ 　　（式3-4）

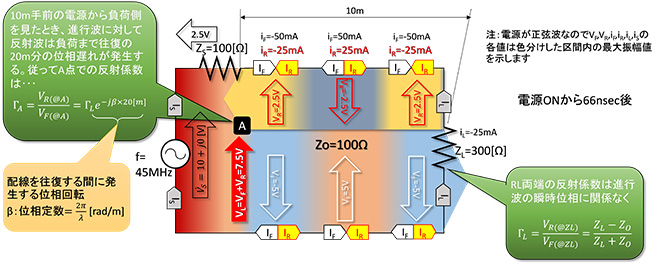
図9　ZSとZLの距離が波長に対して無視できない場合

（3）反射波の位相回転が意味すること
2章で電圧反射係数Γと負荷インピーダンスZLの値は１対１で対応すると説明しました。従って線路上の任意の場所から負荷側を見たときの電圧反射係数Γの値が変化すると云うことは、電源から負荷までの配線（線路）の長さが変わると、電源から見た負荷インピーダンスの値は変化すると言うことになります。

電源から負荷を見たときの反射波電圧の位相変化（＝電圧反射係数の位相変化）の様子をΓ平面で説明すると図10のようになります。配線（線路）が無損失の場合、電源から負荷までの距離が変化すると反射波の振幅は変化せずに位相だけが回転するので電圧反射係数Γは図10に赤の破線で示したように定振幅の円を描きます。そして負荷端から電源を遠ざけた場合、電源から負荷端を見た電圧反射係数ΓはΓ平面を反時計回りに回転し、電源と負荷の間隔がλ/2（電気長）離れる毎に１回転します。

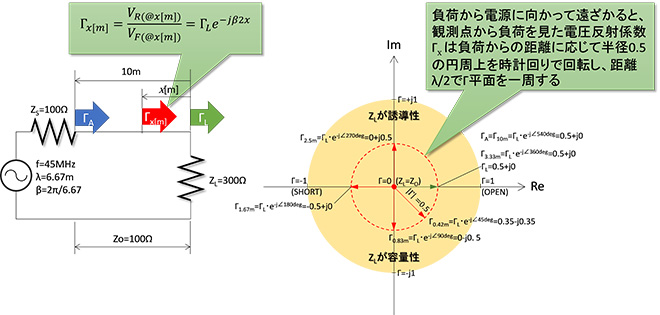
図10　線路長が波長に対して無視できない場合の反射係数Γの変化

このように負荷抵抗と電源の距離が波長に対して無視できない大きさで離れると、電源から見た負荷インピーダンスは本来の負荷が純抵抗であるにも関わらず、両者を結ぶ伝送線路の長さによって、あたかもインダクタンスやキャパシタンスを接続したように見えるのです。長さがλ/4の同軸ケーブルやフィーダー線を先端開放で送信機に接続すると送信機端では短絡されたのと同じ状態になって、送信機を壊してしまう･･･というのはアマチュア無線家の間でもオカルト現象のようによく知られた事ですが、図10においてΓL=1(OPEN)でλ/4電源を遠ざけた状態（=SHORT）と云うことになります。同様に、測定など際に機器間を接続する同軸ケーブルをλ/2の倍数の長さにしておくと反射の影響を受けにくい･･･という経験則も図10においてΓ平面を一周して元の位置に戻ってくる点であることから納得いただけるのではないかと思います。

※2：実際に線路上の電圧をオシロスコープで観測すると進行波電圧と反射波電圧を別々に観測することは不可能で、両者の和の値が観測されます。

4. 第5話のまとめ

第5話では反射係数とスミスチャートの関係を詳しく説明しました。

（1）特性インピーダンスZo（または電源インピーダンスZS）に負荷抵抗ZLを接続した時、ZoとZLの関係で生じる電圧反射係数Γと負荷抵抗ZLは１対１で対応する。
（2）反射係数Γがとり得る値は絶対値１以下の複素平面となり、これをΓ平面と呼ぶ
（3）Γ平面と特性インピーダンスZoで正規化された負荷インピーダンスZLの値を関係づけたチャートがスミスチャートである。
（4）線路の長さ（電源から負荷までの距離）が波長に対して無視できない場合、電源から負荷を見た反射係数は負荷から観測点までの距離に応じてΓ平面（スミスチャート）上を時計回りに回転し、λ/2毎に１周する。

前回、第5話では定在波のお話をすると書きましたが、スミスチャートと反射係数の関係を先に説明したので、またしても定在波まで到達しませんでした。次回こそは定在波とスミスチャートの外周目盛の使い方をご説明したいと考えます。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年3月号トップへ戻る

【第5話】伝送線路と反射係数（その2）

1. 反射係数Γの大きさ

2. スミスチャートの正体

3. 高周波回路のオカルト現象

4. 第5話のまとめ

NEWS

連載記事

テクニカルコーナー

お知らせ

外部リンク