Mr. Smithとインピーダンスマッチングの話／【第8話】直列共振と並列共振｜2019年6月号

Mr. Smithとインピーダンスマッチングの話

【第8話】直列共振と並列共振

濱田倫一

第6話までで「スミスチャートとは何か」と「スミスチャートの使い方」について一通りお話しましたので、第8話以降は高周波回路の設計シーンでエンジニアがよく遭遇する事象について、スミスチャートと関わりのあるものをピックアップしてご紹介していきたいと考えます。今回は反射係数（インピーダンス）の周波数特性についてのお話です。

1. 周波数をスイープしたときのインピーダンス

図1は第5話、第6話と繰り返し登場しますが、おさらいを兼ねての考察です。負荷と電源の間隔が波長に対して無視できない時、負荷端で観測される電圧反射係数ΓLとそこから電源に向かって距離x[m]（またはx[λ]）離れた線路上で観測される電圧反射係数Γxは異なる値になり、図1に示す関係になりました。では、電源の周波数を45MHzから90MHz, 180MHz…と上昇させるとどうなるでしょうか。45MHzを基準に考えたとき、90MHzではλが半分になるのでβは2倍、180MHzでは、λがその半分でβがその2倍…となるので、等価的に線路長を2倍、4倍に延長した、または負荷から遠ざかる距離を2倍、4倍にしたのと同じ結果になります。

つまり、伝送線路を介してあるインピーダンス（図1では300Ω）を観測するとき、観測周波数をスイープすると、その軌跡（frequency Locus）はΓ平面上（すなわちスミスチャート上）を周波数の上昇に伴って時計方向に回転することになります。

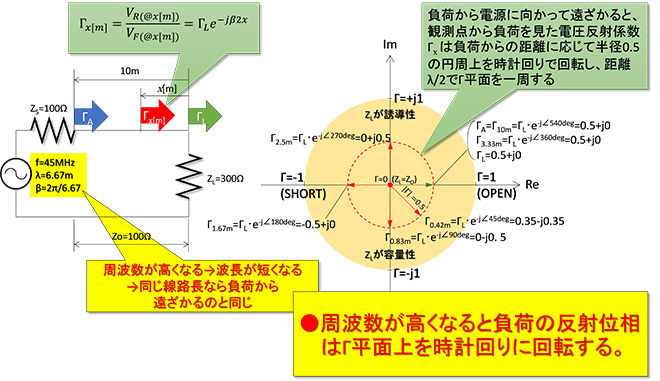
図1　線路長が波長に対して無視できない場合の反射係数Γの変化

この特性はスミスチャート上でインピーダンスの変化を考察するときに重要なポイントになります。

2. 回路素子（L,C）の周波数vsインピーダンス特性

今度は負荷と電源の間隔が波長に対して無視できる時に、理想L,理想Cのインピーダンスの周波数軌跡がどのようになるかをMr.Smithを使用して考察してみましょう。^※1

Mr.Smithでfrequency locusを計算する時は、起動時の「周波数とZ0の設定」ウィンドウ^※2で図2に示すように「frequency sweep」チェックボックスにチェックを入れて、周波数範囲と計算点数の指定を行います。今回は設計ではなく理論考察を行う事が目的なので、周波数範囲をうんと広く、計算点数も多くとりました。

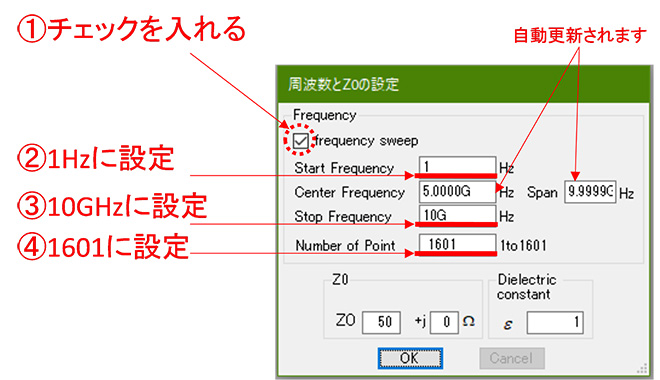
図2　Mr. Smithで周波数スイープ計算する場合の初期設定

※1 Mr. Smith ver3.3のダウンロードはこちらから
※2 「ツール」→「設定」→「計算条件の変更」または
「ファイル」→「新規」またはメインウィンドウ右上（Condition）のChangeボタンでも同じウィンドウが表示さ
れます。

（1） L（インダクタンス）の場合
まずインダクタンスのインピーダンス特性を計算してみましょう。ここでは定性的な考察なので、インダクタンスの値そのものに深い意味はありませんが、（後々事情があって）120nHを例にとって話を進めます。図3に結果を示します。

上のグラフは横軸を周波数、縦軸をリアクタンスとした場合のグラフです。LとｊXの関係は、x=jωL=j2πfLですから、Excelを使えばこのグラフは簡単に作成できます。計算式が示す通り、インダクタンスLの誘導性リアクタンスの大きさは周波数fに比例して単調増加する特性となります。②これをスミスチャート上にプロットするとどうなるでしょうか。

理想インダクタンスの直流インピーダンスは0Ωなので、Mr.Smithでインダクタ単体のインピーダンスを計算する時は図3左下に示すように0Ωに120nHを直列接続するのが、（マーカ位置が連続するので）判りやすいと思います。^※3

Mr.Smith上では△が1Hz、○が「display frq」リストで選択している周波数、×が10GHzになります。120nHの周波数軌跡は0Ωを起点とし、1章で述べたとおり、周波数上昇と共にスミスチャートの外周を時計回りに回転し、∞Ωに近づいてゆきます。但し、Stop Frequencyを100GHz、1000GHzと変更して試して頂けば判るとおり、伝送線路上を負荷から遠ざかる場合と違ってどれだけ周波数が高くなっても∞Ωを超えて回転することはありません。

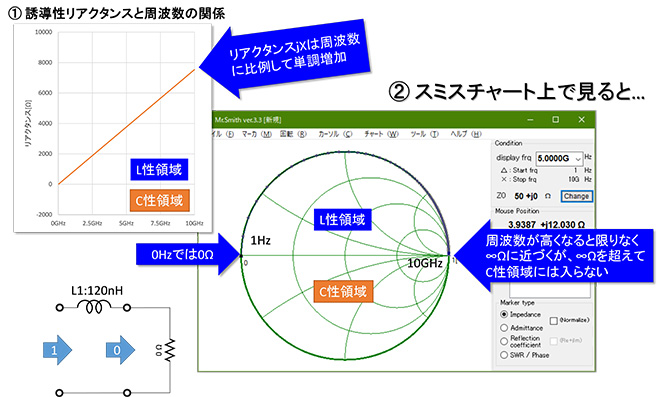
図3　理想インダクタンス(120nH)の周波数軌跡

（2） C（キャパシタンス）の場合
次にキャパシタンスのインピーダンス特性を計算してみましょう。ここでもキャパシタンスの値そのものに深い意味はありませんが、（後々事情があって）5.1pFを例にとって話を進めます。図4に結果を示します。
①左上のグラフは横軸を周波数、縦軸をリアクタンスとした場合のグラフです。Cとjxの関係は、 $x + \frac{1}{jωC} = j \frac{1}{2πjωC}$ ですから、Excelを使えばこのグラフは簡単に作成できます。計算式が示す通り、キャパシタンスCの容量性リアクタンスの絶対値は $\frac{1}{f}$ に比例して減少し0Ωに漸近する特性となります。②これをスミスチャート上にプロットするとどうなるでしょうか。理想キャパシタンスの直流インピーダンスは∞Ωなので、Mr.Smithでキャパシタ単体のインピーダンスを計算する時は図4左下に示すように0S（∞Ω）に5.1pFを並列接続するのが、（マーカ位置が連続するので）判りやすいと思います。^※3

Mr.Smith上では△が1Hz、○が「display frq」リストで選択している周波数、×が10GHzになります。5.1pFの周波数軌跡は∞Ωを起点とし、1章で述べたとおり、周波数上昇と共にスミスチャートの外周を時計回りに回転し、0Ωに近づいてゆきます。但し、Stop Frequencyを100GHz、1000GHzと変更して試して頂けば判るとおり、伝送線路上を負荷から遠ざかる場合と違ってどれだけ周波数が高くなっても0Ωを超えて回転することはありません。

図4　理想キャパシタンス(5.1pF)の周波数軌跡

※3　1素子しかないので、直列で計算しても並列で計算しても同じ結果になります。

（3）理想直列共振回路の場合
今度は理想直列共振回路です。ご周知の通り、共振回路の共振周波数はf0= $\frac{1}{2 π \sqrt{LC}}$ で求まり、前述のL=120nH、C=5.1pFの組み合わせで共振回路を構成すると、f0=約200MHzとなります。

図5に結果を示します。①左上のグラフは横軸を周波数、縦軸をリアクタンスとした場合のグラフです。イメージを掴みやすくするために|X|のグラフも一緒にプロットしました。f0でリアクタンスが0Ωになっている様子がお解りいただけると思います。②これをスミスチャート上にプロットするとどうなるでしょうか。120nH+5.1pFの直列共振回路の周波数軌跡は∞Ωを起点とし、やはり時計回りで最初は51pFのリアクタンス特性と同じ軌跡を描きますが、5.1pFでは超えることがなかった0Ωを共振周波数のポイントで通り超え、その先は120nHのリアクタンス特性と同じ軌跡に合流します。従って周波数上昇と共にスミスチャートの外周を時計回りに回転し、∞Ωに近づいてゆき、伝送線路上を負荷から遠ざかる場合と違ってどれだけ周波数が高くなっても∞Ωを超えて回転することはありません。

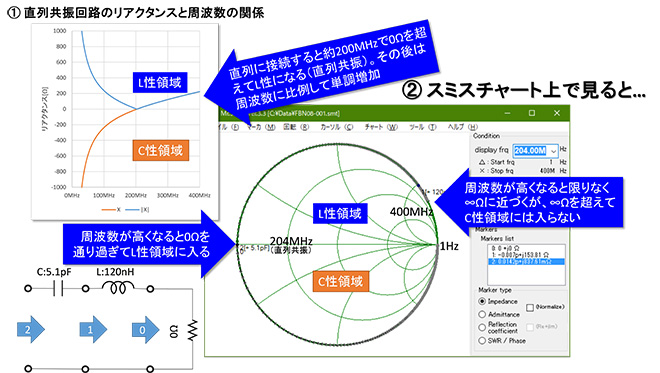
図5　理想直列共振回路(120nH+5.1pF)の周波数軌跡

（4）理想並列共振回路の場合
今度は理想並列共振回路です。直列共振と同様、120nH//5.1pFで考察します。図6に結果を示します。①左上のグラフは横軸を周波数、縦軸をリアクタンスとした場合のグラフです。イメージを掴みやすくするために|X|のグラフも一緒にプロットしました。f0でリアクタンスが+∞Ωになった後-∞に転じている様子がお解りいただけると思います。②これをスミスチャート上にプロットするとどうなるでしょうか。120nH+5.1pFの並列共振回路の周波数軌跡は0Ωを起点とし、やはり時計回りで最初は120nHのリアクタンス特性と同じ軌跡を描きますが、120nHでは超えることがなかった∞Ωを共振周波数のポイントで通り超え、その先は5.1pFのリアクタンス特性と同じ軌跡に合流します。従って周波数上昇と共にスミスチャートの外周を時計回りに回転し、0Ωに近づいてゆき、伝送線路上を負荷から遠ざかる場合と違ってどれだけ周波数が高くなっても0Ωを超えて回転することはありません。

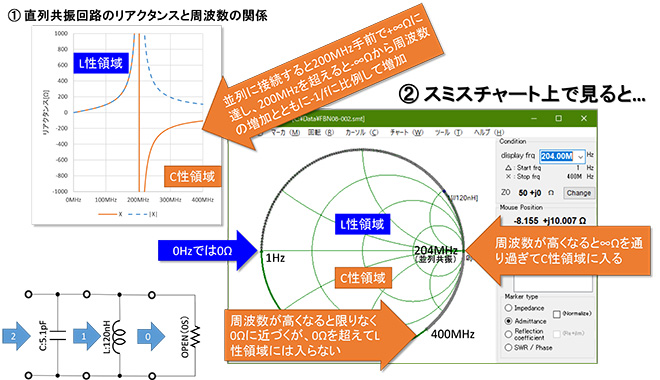
図6　理想並列共振回路(120nH//5.1pF)の周波数軌跡

（5）直列共振回路の並列接続と並列共振回路の直列接続
ここまでの話を少し整理してみましょう。
①　あるインピーダンスを伝送線路を介して観察したとき、その観察値は周波数の上昇につれてスミスチャート上を時計方向に回転する
②　理想C、理想Lのインピーダンス（リアクタンス）は周波数の上昇につれてスミスチャートの最外周を時計方向に回転するが、それぞれ0Ωと∞Ωを超える事はない。
③　理想直列共振回路では共振周波数以下の周波数帯ではCと同様に振る舞い、共振周波数で0Ωとなり、共振周波数より高い周波数ではLと同様の振る舞いになる。
④　理想並列共振回路では共振周波数以下の周波数帯ではLと同様に振る舞い、共振周波数で∞Ωとなり、共振周波数より高い周波数ではCと同様の振る舞いになる。

となります。③④をもう少し整理すると、
⑤　周波数軌跡がC性領域からL性領域に跨がって変化（回転）しているときは直列共振が起きており、共振周波数はX=0Ωの等リアクタンス円（純抵抗の目盛）と公差するポイントである。
⑥　周波数軌跡がL性領域からC性領域に跨がって変化（回転）しているときは並列共振が起きており、共振周波数はX=0Ωの等リアクタンス円（純抵抗の目盛）交差するポイントである。
と言うことになります。

だとすると①の伝送線路を介して見たインピーダンスは、周波数が上昇するに伴って、スミスチャート上を何周もすることになりますから、直列共振と並列共振を繰り返している…ということになるのですが、どのような回路に見えているのでしょうか。

周波数の上昇に伴って、直列共振と並列共振を繰り返す回路は、図7に示すような直列共振回路の並列接続回路、または並列共振回路の直列接続回路に置き換えることができます。

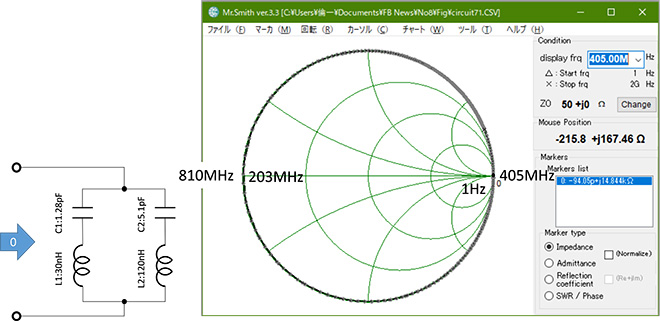
図7　直列共振回路の並列接続回路

残念ながらMr. Smithではこの回路のインピーダンス特性の周波数軌跡は直接計算できません^※4。図7の周波数軌跡は回路シミュレータMicro-CAP12^※5でインピーダンス計算した結果をCSV形式で出力し、Excelでフォーマット加工してMr. Smithに読み込んだものです。

図7の回路は共振周波数813MHzの共振回路（L1+C1）と203MHzの共振回路（L2+C2）を並列に接続した回路です。この回路の合成インピーダンスの周波数軌跡は直流では∞Ω、周波数の上昇につれてチャートの外周を時計方向に回転して203MHzで最初の直列共振、405MHzで並列共振、約810MHzで2度目の直列共振を生じます。なぜこのような特性になるかを図解したのが図8です。共振周波数の異なる共振回路を複数接続すると、各共振器の共振周波数の中間でも共振が発生します。

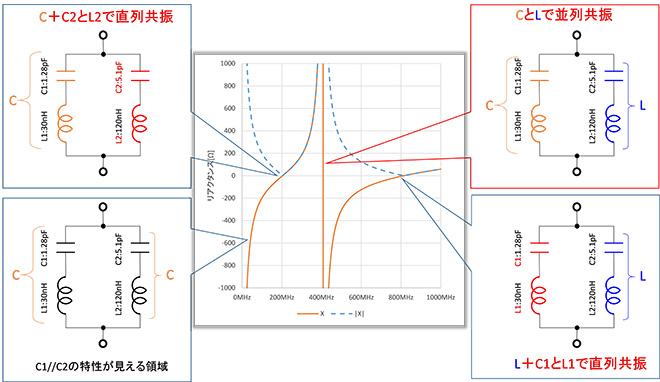
図8　共振周波数の異なる直列共振回路を並列接続したときの動作

なお並列共振回路を直列接続した場合は、直流での合成インピーダンスが0Ωとなり、並列共振と直列共振の順番が逆になります。

※4　単周波数なら、最初に直列共振回路のインピーダンスを求めた上で、「回転」→「Complex Element」→「Parallel Z」メニューで求めたインピーダンスを直接入力することにより、計算可能です。
※5　https://www.toyo.co.jp/mecha/products/detail/ssw-mc12.html#link22

3. 理想の回路素子と実際の回路素子の関係

我々が回路図上で取り扱うL,C,Rと呼ぶデバイスは、実は物理的な大きさがゼロでなければ実現することができません。1章で述べた通り、インピーダンスの観測点から回路素子までの距離が有限の長さを持っていると、その長さが波長に対して無視できる領域（進行波と反射波の位相差が0°と見なせる領域）では、回路素子のインピーダンスは教科書通りに観測されますが、波長に対して無視できない領域（周波数）になると、周波数の上昇に伴って、進行波と反射波の位相差が負荷インピーダンスの特性に関係なく広がっていく為、周波数の上昇に伴ってスミスチャート上を回転することになります（→図9～11）。つまりL,C,Rと呼んでいる全てのデバイスが多段接続された共振回路に見える事になるのです。進行波と反射波の位相関係が負荷インピーダンスに関係なく変化する要因は、デバイスの電極から観測点までの距離に限った事ではなくデバイスそのものの大きさ、電極間の距離、巻線や抵抗体の長さでも同様に発生します。

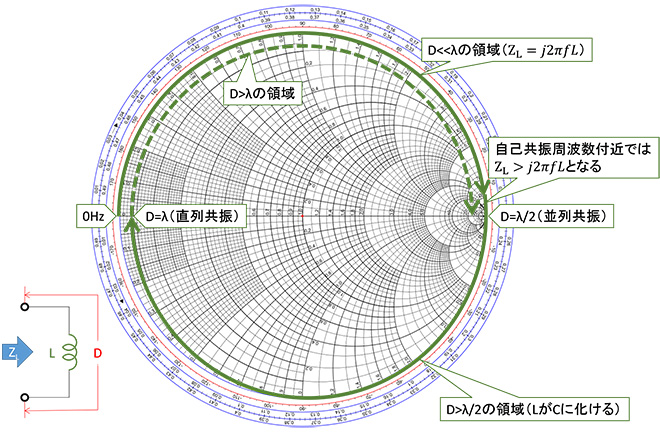
図9　実際のLの周波数 vs インピーダンス軌跡（イメージ）

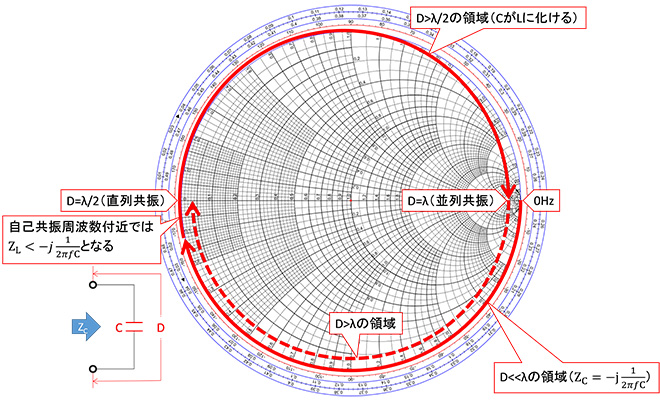
図10　実際のCの周波数 vs インピーダンス軌跡（イメージ）

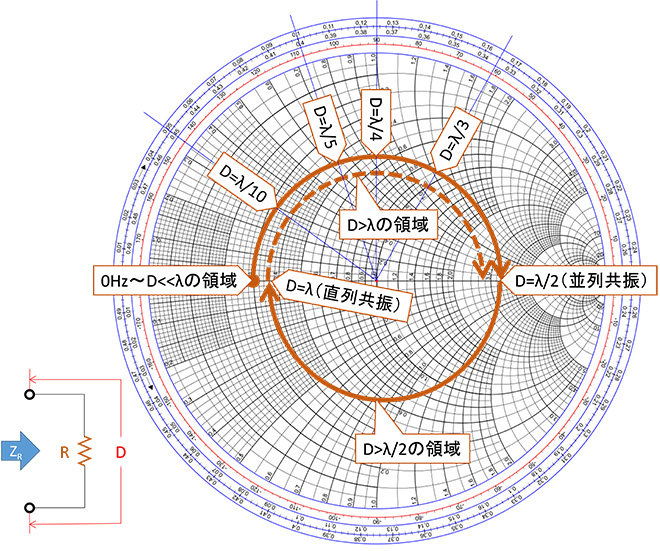
図11　実際のRの周波数 vs インピーダンス軌跡（R=0.3×50Ωの場合、イメージ）

このように、私たちが普段取り扱うL,C,Rは部品毎にL,C,Rとして機能できる上限周波数があり、メーカのデータシートには「自己共振周波数」というパラメータで表示されています。自己共振周波数を超えてLがCに、あるいはCがLに化けた領域では、そのデバイスのインピーダンスは、元のインダクタンスやキャパシタンスに関係なく、そのデバイスの端子間の電気長で概ね決定されてしまいます^※6。つまりこのことは図9～11に示したDの値が小さいほど、高い周波数まで理想のL,C,Rとして利用可能であることを示しています。近年、無線機器の高周波化が進みましたが、それを可能にしたのは部品の小型化であると言っても過言ではありません。

※6　実際の電子デバイスは、損失や電極間距離以外の要因で発生する寄生共振の影響で、自己共振周波数以上の周波数域では、もっと複雑な周波数軌跡を描きます。

4. 第8話のまとめ

第8話では反射係数の周波数軌跡の初歩として、理想L,Cのインピーダンス軌跡と共振回路のインピーダンス軌跡、ならびに実際のデバイスのインピーダンス vs 周波数特性がどのように見えるのかについて解説しました。要点をまとめると以下の通りです。
①　一般論として、あるデバイスのインピーダンスの周波数軌跡は周波数の上昇に伴ってスミスチャート上を時計方向に回転する。
②　理想L、理想Cの周波数vsインピーダンス軌跡はスミスチャートの外周を時計方向に回転するが半周以上は回転しない。
③　共振回路の周波数vsインピーダンス特性は、スミスチャートの外周を半周以上進む。この時、スミスチャートの左半円で実抵抗軸と交差する点が直列共振周波数、右半円で交差する点が並列共振周波数となる。
④　デバイスを理想のL,C,Rとして取り扱えるのは、そのデバイスの端子間の電気長が波長に対して十分に無視できる範囲（例えばλ/360以下）の周波数までであり、それを超えると反射波の位相回転の影響（＝共振特性の影響）が見えてくる。
⑤　さらにそのデバイスの端子間の電気長がλ/4に達すると共振し、λ/2を超えると共振回路の多段接続に見える

実際の電子デバイスは、損失や電極間距離以外の要因で発生する寄生共振の影響で、自己共振周波数以上の周波数域では、もっと複雑な周波数軌跡を描きます。次回はこのあたりを中心に解説します。

Mr. Smithとインピーダンスマッチングの話　バックナンバー

2019年6月号トップへ戻る

【第8話】直列共振と並列共振

1. 周波数をスイープしたときのインピーダンス

2. 回路素子（L,C）の周波数vsインピーダンス特性

3. 理想の回路素子と実際の回路素子の関係

4. 第8話のまとめ

NEWS

連載記事

テクニカルコーナー

お知らせ

外部リンク