Mr. Smithとインピーダンスマッチングの話
【第6話】スミスチャートとは何か(その2)
電気の伝わり方の説明に時間を要してしまいましたが、ようやく第三話の続き「スミスチャートとは何か」の後半のお話です。第3話ではスミスチャートでL,C,Rの直並列接続を取り扱う方法をご説明しました。第4話~第5話で反射係数のお話をして、スミスチャートとは反射係数Γの複素平面にインピーダンスの目盛を引いたものであることはご理解いただけたと思います。第六話でお話しするスミスチャートの外周の目盛は、このΓ平面に関する目盛になります。
1.負荷から遠ざかった時のインピーダンスを知る方法
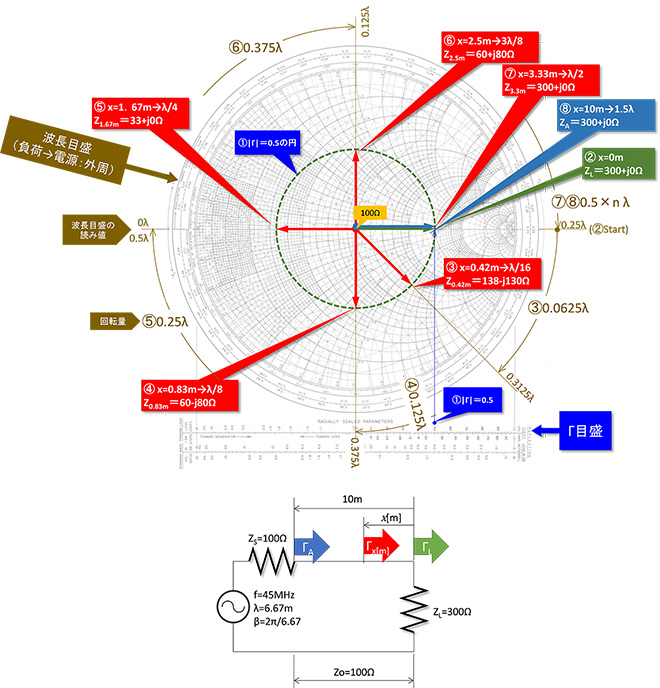
図1は第5話のおさらいです。負荷と電源の間隔が波長に対して無視できなくなると、負荷端で観測される電圧反射係数ΓLとそこから電源に向かって距離x[m](またはx[λ])離れた線路上で観測される電圧反射係数Γxは異なる値になります。これは進行波を基準としたときの反射波の位相が電源と負荷の間を接続する伝送線路の長さ※の関数になることが理由で、負荷からの距離に応じて図1右側のΓ平面に示すように絶対値一定で時計回りに回転します。負荷から観測点までの長さと回転量(角度)の関係は0.5λで1回転(2πrad)でした。
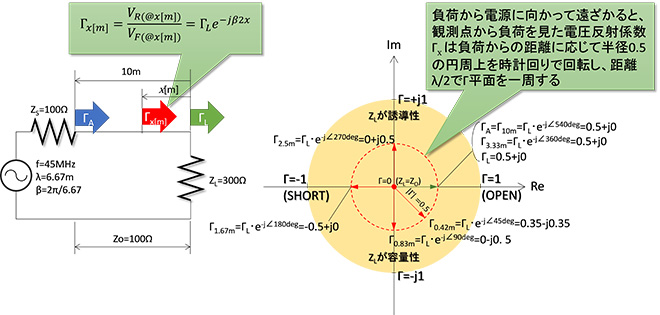
図1 線路長が波長に対して無視できない場合の反射係数Γの変化
負荷からの距離に応じて電圧反射係数Γがこのように変化したときの観測点から見た負荷インピーダンスはスミスチャートを用いて導出することができます。市販のスミスチャートには、図2に示すようなΓ平面に関する目盛があり、この目盛を使用して電圧反射係数Γの値をインピーダンスチャート上に直接プロットすることができます。
※ここで云う「長さ」は電気長の事で、物理長(物差しで測った長さ)を波長短縮率で割った値です。
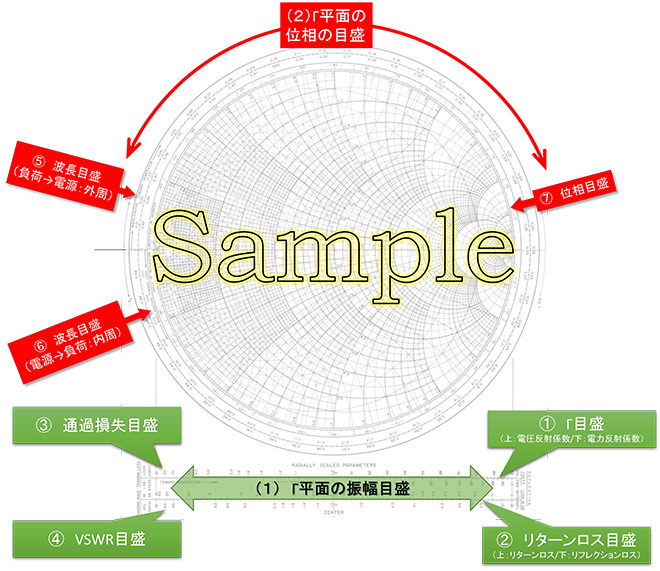
図1 市販のスミスチャートのΓ平面に関する目盛
(1)Γ平面の振幅目盛
図2に示す通り、市販のチャートにはチャートの下部にスミスチャートをΓ平面と見立てた時の振幅軸プロット用の目盛がついています。チャートによって様々な目盛があるのですが、どのチャートにも必ずついているのが①Γ、②リターンロス、④VSWRの各目盛です。
①Γ目盛:電圧反射係数Γを極座標でプロットするときに使用する振幅目盛です。図2のサンプルでは電圧反射係数と電力反射係数の2つの目盛が準備されています。電圧反射係数Γは中心が0で円周部が1のリニアな目盛です。
②リターンロス(RL)目盛:図2ではリターンロス(RL)とリフレクションロスをdBで表した目盛となっています。両者の違いは以下の通りです。よく混同されていますので注意が必要です。
・リターンロス(RL):電圧反射係数|Γ|を20logのdB表記とした値です。直訳すると「反射電力の損失」を表すことになり、0dBで全反射を示します。通常”RL”と表記するとReturn Lossを示します。
・リフレクションロス:負荷電圧と進行波電圧の比を20logのdB表記とした値です。0dBで無反射を表します。
③通過損失目盛:伝送方向の損失係数です。結果的にリフレクションロスと同義です。
④VSWR目盛:VSWR値をプロットするときに使用する目盛です。
(2)Γ平面の位相目盛
チャートの外周にはスミスチャートをΓ平面と見立てたときの位相(角度)目盛が通常3種類ついています。
⑤負荷から電源方向の波長目盛:”Wave length toward generator”と書かれた時計回りに増加する目盛で、伝送線路上を負荷端から電源に向かって離れていく際の距離を波長比で表した目盛です。0.5λでチャートを1周します。
⑥電源から負荷方向の波長目盛:”Wave length toward load”と書かれた反時計回りに増加する目盛で、伝送線路上を電源から負荷に向かって離れていく時の距離を波長比で表した目盛です。①と同様、0.5λでチャートを1周します。
⑦角度目盛:電圧反射係数カΓを極座標でプロットする際に使用する角度目盛です。
(3)Γ平面目盛の使用例
図1に示した例を実際にスミスチャートにプロットして、線路の長さが変化した時のインピーダンスの変化を導出したのが図3です。
①Γの軌跡
図1の例では電圧反射係数の絶対値|Γ|=0.5なので、線路上の任意の点における電圧反射係数Γは、スミスチャート下部のΓ目盛で0-0.5間の長さを半径とする円(図中の黒破線の円)上に存在し、負荷端から電源に向かって移動したときは、この円上を時計方向に回転します。
②ΓL
図1の回路ではZLが純抵抗、かつZL>ZSなので負荷抵抗ZLからの距離=0mのとき、進行波と反射波の位相差は0°(同相)になります。半径0.5、角度0°の点はスミスチャートの目盛から3Ωと読めます。この回路ではZO=100Ωなので、ZL=300Ωとなります。
③Γ0.42m
周波数45MHzの交流信号の波長λは6.67m、従って負荷から0.42mの距離は波長比でλ/16=0.0625λとなります。この点での電圧反射係数Γ0.42mはΓLから時計回りにWave length toward generatorと書かれた波長目盛(外周の目盛、時計回り)で0.0625回転したところにあります。この位置から負荷方向を見た時のインピーダンスZ0.42mは、チャートの-1.4の等リアクタンス円と1.3の等レジスタンス円の交点にありますので、140-j130[Ω]に見える と言うことになります。なお図3では③Z0.42m=138-j130Ωと書いていますが、これは後述のMr. Smithで求めた値です。以下、同様に④⑤⑥⑦・・・と負荷インピーダンスZLを導出することが可能です。負荷ZLからλ/2離れたところでインピーダンスの値が元に戻ることが判ります。
⑧ΓA(④~⑦は省略)
最後に負荷から10m離れた電源端から負荷を見た時のインピーダンスZAですが、負荷から電源までの距離10mは波長比で1.5λとなります。従って電圧反射係数|Γ|のベクトルはスミスチャートを3周して元の位置(角度0°)の位置に戻り、ZA=300Ωとなります。なお、ここまでの話は10mの線路に損失が無い場合の話です。線路に損失があると(あるのが普通ですが)|Γ|の大きさは損失分だけ小さくなる(図3の黒破線の円の半径が徐々に小さくなる)為、⑧の位置ではZA=300Ωとは見えず、実際にはもう少し小さい値になります。
2.Mr.Smithで計算するには
以上が市販のスミスチャートによる反射係数の計算ですが、Mr. Smithでも同様の計算が可能です。図1の計算をMr. Smithで行う手順は以下の通りです※。
※Mr. Smithはこちらからダウンロード可能です
(http://www.fbnews.jp/201812/mrsmith/images/mr_smith_setup_v3_3.zip)
(1)線路の特性インピーダンスと周波数の指定
Mr. Smith起動時に表示される”周波数とZOの設定”ウィンドウで、①電源周波数=45MHzと線路の②特性インピーダンス(100Ω)を設定します。→図4
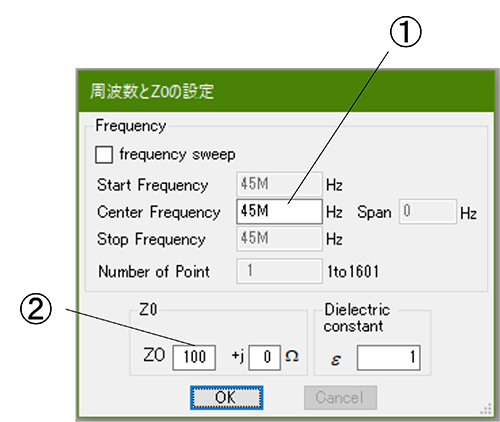
図4 周波数とZO設定画面
(2)ZLマーカの設定
Mr.Smithのメインウィンドウが表示されたら周波数が45MHz、ZOが100Ωであることを確認し、③「マーカ」「Reflection Coefficient」を選択して④開いたマーカ設定ウィンドウに0.5U∠0degを入力してOKボタンをクリックします※。→図5
※「マーカ」「Impedance R+jX」を選択して300Ωと入力しても同じ結果になります。
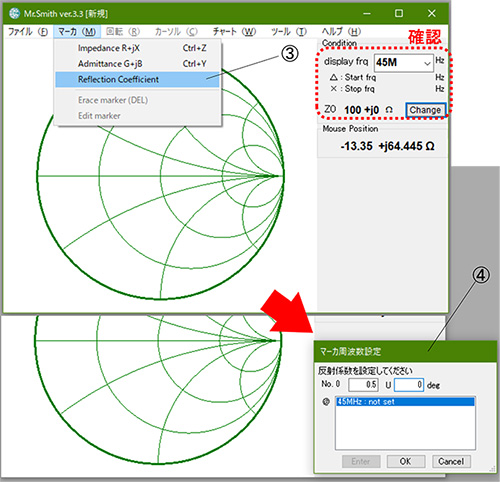
図5 ZLマーカの設定
(3)インピーダンスに換算
ZLマーカを反射係数で入力した場合は、Markers listボックスは-6.02dB∠0degというふうに反射係数の大きさ(RL表記)が表示されている筈です。この値をインピーダンスに換算するには⑤Marker typeラジオボタンから”Impedance”を選択します※。→図6
※「マーカ」「Impedance R+jX」を選択して300Ωと入力した場合は、"Reflection coefficient"を選択することで反射係数に変換することができます。
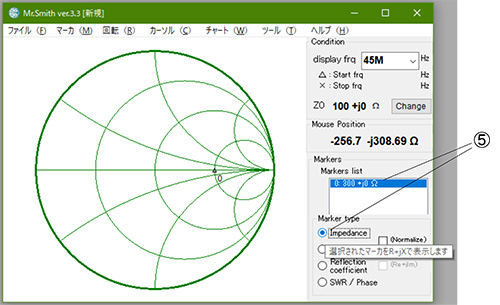
図6 反射係数→インピーダンス変換
(4)電源に向かって移動
電源に向かって伝送線路上を移動したときのインピーダンスの変化は、Mr.Smithでは「ZLに100Ωの伝送線路を接続する」というオペレーションで計算します。具体的には、Markers listボックスでZL(図では0番マーカ)が選択されている状態で、⑥「回転」→「Connect line」→「Electrical length[λ]」と選択し、開いたウィンドウから⑦100Ω/0.0625λと入力、OKボタンを押すことで、Γ0.42mの値を求めることができます※。→図7
※波長と物理長の関係は表1を参照。線路長は「Physical length[m]」を選択して100Ω/0.42mと入力しても同じ結果が得られます。但し、実際の線路(フィーダー線や同軸ケーブル)では波長短縮がかかるので、あらかじめ図4のウィンドウでεに使用する線路の実効誘電率を設定しておく必要があります。(デフォルト値はε=1(自由空間)です。)
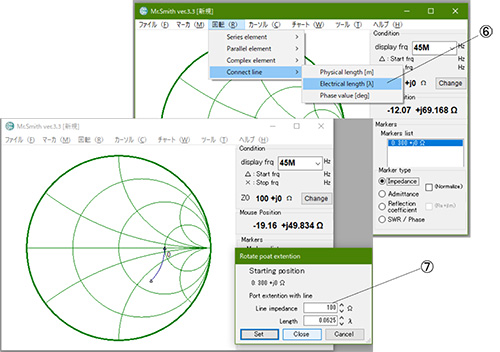
図7 電源に向かって0.42m移動(=線路の接続)
Γ0.42mの値は1番マーカの表示となります⑨ これをインピーダンスの値に変換するのは(3)と同一の手順によります。→図8⑧⑨
以下、同じ手順でΓ0.83m、Γ1.67m、Γ2.5m、Γ3.33mを計算した結果を図9に示します。ここでは図7⑦と同様、負荷からの距離を波長に換算してλで入力しています。ご周知の事と思いますが、両者は(式2-1)に示す関係で、表1の通りです。
(式2-1)
表1 波長と物理長の関係(45MHz)

複数あるマーカは何れも0番マーカに0.83m、1.67m、2.5m、3.33mの線路を接続した結果を示します(都度マーカ0を選択してから回転メニューを選択)。ΓAは、負荷から1.5λ離れた距離となるので、チャート上を1.5周して0番マーカに戻ります。
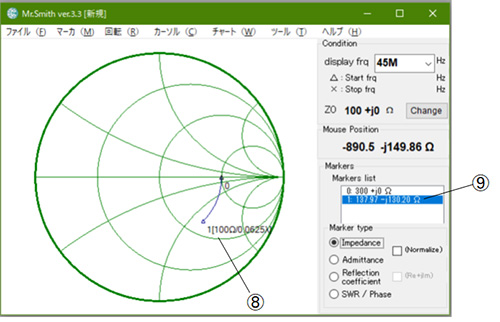
図8 電源に向かって0.42m移動(=Lineの接続)
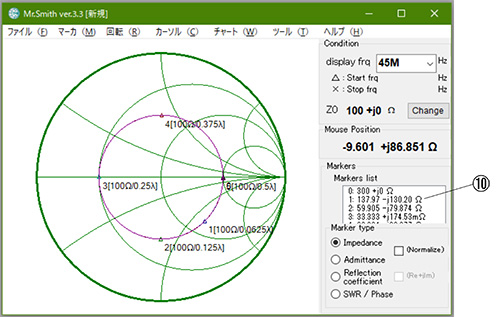
図9 負荷から0.83m、1.67m、2.5m、3.33m離れた地点での負荷インピーダンス
3.インピーダンスの測定とスミスチャートとVSWR
ここまでのお話で以下の事が理解いただけたと思います。電圧反射係数Γはインピーダンスと1対1で対応しており、例えば送信機出力コネクタで測定したΓをスミスチャート上にプロットし、給電線の長さ(電気長)分だけ、反時計回り(TOWARD ROAD目盛の方向)に回転するとアンテナの放射インピーダンスが求められる事になります。
逆にインピーダンスが既知のデバイスにマイクロストリップラインなどの伝送線路を接続して一定の長さまで離れたときのインピーダンスは、スミスチャート上でそのインピーダンスを時計回り(TOWARD GENERATOR目盛の方向)に回転すれば求める事ができます。
本来スミスチャートとは、このように電圧反射係数を測定し、観測点から負荷までの距離から負荷インピーダンスを導出する為に考案された図表なのです。昨今ではベクトルネットワークアナライザが普及して、電圧反射係数Γの測定が簡単にできるようになりましたので、アンテナを含む高周波インピーダンスは、ほとんどこの方法で計測されています。
次は昔話を少し・・・
(1)インピーダンス測定の今昔
ようやくVSWRの話です。私が現役設計者の頃(いまでも一応現役ですが、少し偉くなりました)、ベクトルネットワークアナライザ(以下VNA)が初めて1000万円を切りました。それでもスペアナの2~3倍の価格でした。私たちの諸先輩の時代、VNAは3000万~6000万円していましたから、容易に利用できる測定環境ではありませんでした。まして私たちの大先輩の時代には高周波のベクトル電圧を正確に測定する技術がありませんでした※。従って、電圧反射係数Γを測定するのは極めて困難でした。そこでRL(Return loss)とVSWRという概念が登場します。RLは1.(1)で説明した通り、電圧反射係数の絶対値|Γ|を20logのdB表記とした値です。この値は方向性結合器を使用すれば電力計やスペアナで容易に測定できますが、残念ながら位相の情報が無いので反射の大きさは判ってもインピーダンスを求める事はできません。そこで電圧定在波の大きさからインピーダンスを求める事が考えられました。
※当然理論はありました
(2)定在波とは何か
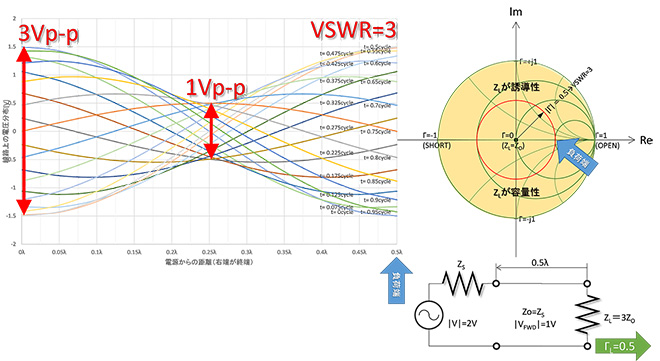
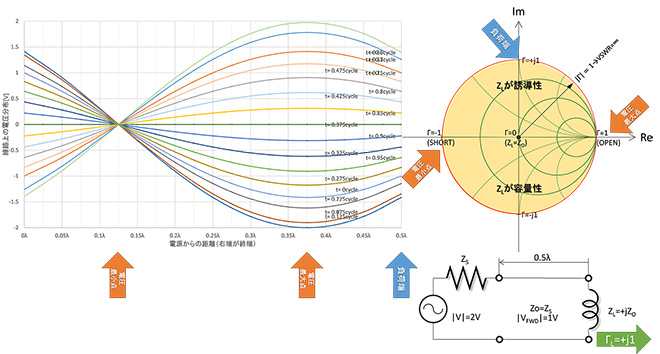
線路上に進行波と反射波が存在すると、両者が干渉するため線路上の電圧振幅は負荷(反射点)からの距離によって波状に変化します。この電圧振幅の変化の波を電圧定在波(Voltage Standing Wave)と呼びます。図10は図1と同じZS=ZO=100Ω、ZL=300Ωで、電源から負荷までの線路長が0.5λの場合に線路上に発生する定在波(電圧振幅の分布)を計算したものです。線路上の任意の場所の電圧は進行波電圧と反射波電圧の和になるので、定在波の振幅は進行波と反射波の位相が同相となる部分が最大、逆相となる部分が最小で、負荷の反射係数が大きくなるほど最大値と最小値の差が大きくなり、全反射(|Γ|=1)の時、最大値は進行波電圧の2倍、最小値は0となります。図10では|Γ|=0.5なので、定在波の最大値は進行波の1.5倍、最小値は0.5となっていることが判ります。
この線路上の振幅電圧の最大値と最小値の比を電圧定在波比VSWR(Voltage Standing Wave Ratio)と云い、|Γ|=0でVSWR=0、|Γ|=1でVSWR=∞となるので、反射波の大きさ(すなわち負荷の整合状態)を表す指数として用いられます。図10の場合は
VSWR=(線路上の最大振幅/線路上の最小振幅)= 3[Vp-p]/1[Vp-p] = 3 (式3-1)
となります。またVSWRと電圧反射係数Γは(式3-2)に示す関係になります。
(式3-2)
従って、VSWRもRLと同様、スカラー量であり位相の情報は含まれません。スミスチャート上ではZOを中心とする円となります。
(3)VSWRから負荷インピーダンスを知る方法
ここまで書くと「じゃあ結局VSWRを計ったところでインピーダンスは求められないじゃないか・・・」とお叱りをうけそうです。VSWRをRLから換算しただけの場合はその通りで、単純にインピーダンス整合状態の指標(反射波の大きさの指標)にしかなりません。本来、VSWRは高周波電圧計を用いて線路上の高周波電圧の分布を測定して求めていました。図10のグラフをよく見て頂くと判りますが、線路上の電圧振幅最大点と最小点は必ず異なる場所に(正確に言うとλ/4の間隔で)発生します。この電圧最大点と最小点が発生する場所は負荷端の電圧反射係数Γの位相(=進行波と反射波の位相差)で変化します。この様子を図11~14を使って説明します。ここでは第5話の説明と揃えるのと、話を判りやすくする趣旨で、|Γ|=1(全反射)の状態で計算した結果を示しました。
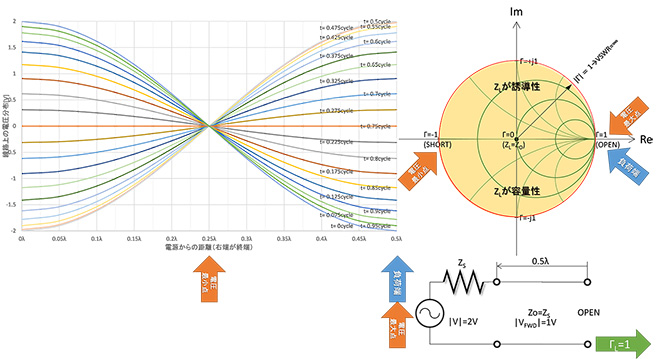
①負荷を開放にしたとき
図11に示す通り、負荷を開放にすると電圧最小点(0V)は負荷から電源に向かってλ/4遡ったところに発生します。
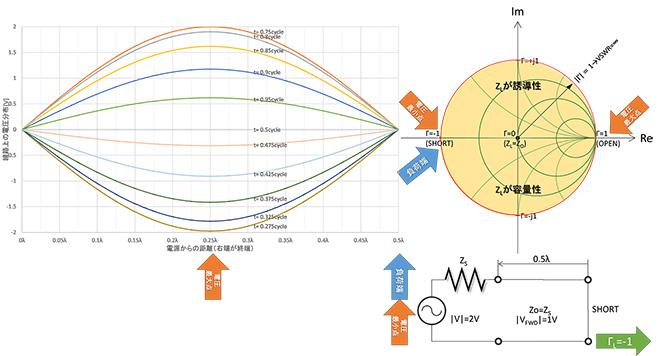
②負荷を短絡したとき
負荷を短絡にすると、図12に示すように電圧最小点(0V)は負荷端に現れ、負荷から電源に向かってλ/4遡ったところには電圧最大点が発生します。
③負荷に0+jZOΩを接続したとき
今度は誘導性負荷を接続した場合です。第5話で説明した通り、負荷に+jZOΩを接続すると反射係数は+j1となりました。この時の定在波は図13に示すように電圧最小点(0V)が負荷端から3λ/4の位置に現れ、負荷から電源に向かってλ/8遡ったところに電圧最大点が発生します。
④負荷に-jZOΩを接続したとき
最後は容量性負荷を接続した場合です。第5話で説明した通り、負荷に-jZOΩを接続すると反射係数は-j1となりました。この時の定在波は図14に示すように電圧最小点(0V)が負荷端からλ/8の位置に現れ、負荷から電源に向かって3λ/4遡ったところに電圧最大点が発生します。
⑤電圧最小点と電圧最大点の意味
ここまで説明すると察しの良い方はお分かりになったのではないかと思います。定在波の電圧最大点、最小点はスミスチャート上の実抵抗目盛(上下中央の線)上に存在し、電圧最小点がZOよりも左側(R<ZO)、電圧最大点がZOよりも右側(R>ZO)になります。従って、
i) チャートに付属しているVSWR目盛(図2参照)を用いて、定VSWR円の半径を導出してプロットする →図15
ii) 負荷から電圧最小点(最大点)から負荷端までの長さを測定して波長比に換算
iii)定VSWR上を、電圧最小点(電圧最大点)から"WAVELENGTH TOWARD LOAD目盛"の方向にii)で求めた長さ分辿ったところが負荷のインピーダンスになる
という手順で負荷インピーダンスを知ることができます。
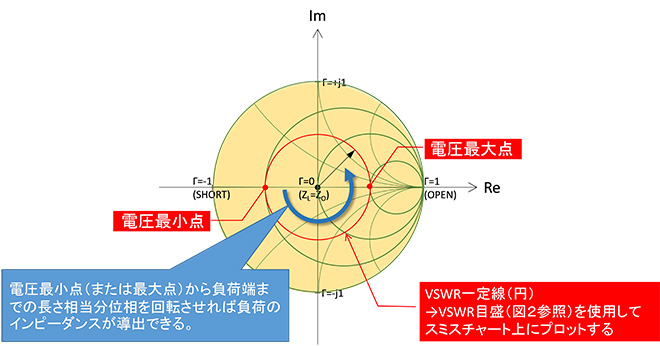
図15 電圧最大点、最小点とインピーダンスの関係
これがスミスチャートの最初の使われ方だったのですが・・・ いやはや昔の人は苦労されたんだなあ・・・ と感慨にふけってしまいます。この測定方法は電圧の最大点、最小点を精度良く求めるのが難しく、さらに給電線路のほとんどが同軸ケーブルになって、線路上の電圧測定そのものが困難になった昨今では、殆ど使用されなくなってしまいましたが、昔からの慣習でRLと同義のVSWRが相変わらずインピーダンス整合の指標として使用され続けています。
4.第6話のまとめ
第6話ではスミスチャートの反射係数関連の目盛の説明と具体的な使い方をご説明しました。
(1)電源から負荷までの距離が波長に対して無視できないときの、線路上の任意の点で観測したインピーダンスは、スミスチャートに|Γ|一定円をプロットして求める事ができる。
(2)上記は負荷で観測した反射係数を基準に線路長を補正する場合は時計方向、電源で観測した反射係数を基準に線路長を補正する場合は反時計方向に|Γ|一定円上を辿る。
(3)電圧定在波とは進行波と反射波が干渉して線路上に波状に発生する電圧分布のこと。
(4)電圧定在波比(定在波の最大値と最小値の比)は|Γ|と同義だが、電圧最小点、最大点の位置が判れば、そこから負荷端までの長さから、スミスチャートを用いて負荷インピーダンスを算出することができる。
ここまでで、スミスチャートの基本的な使い方は全てご説明したことになります。如何でしたか?スミスチャートと高周波の伝搬についてご理解頂けましたでしょうか?
次回は技術解説から少し離れて、スミスチャートの歴史をご紹介します。
Mr. Smithとインピーダンスマッチングの話 バックナンバー
- 【第40話】 (連載最終話) インピーダンスマッチングの四方山話
- 【第39話】 アンテナと空間のインピーダンス(その6 平衡と不平衡(その2))
- 【第38話】 アンテナと空間のインピーダンス(その6 平衡と不平衡(その1))
- 【第37話】 アンテナと空間のインピーダンス(その5 放射抵抗と給電抵抗)
- 【第36話】 アンテナと空間のインピーダンス(その4 アンテナの放射抵抗)
- 【第35話】 アンテナと空間のインピーダンス(その3 放射電力と空間のインピーダンス)
- 【第34話】 アンテナと空間のインピーダンス(その2 ダイポールアンテナ)
- 【第33話】 アンテナと空間のインピーダンス(その1 電磁波とは何か)
- 【第32話】 低雑音増幅器(LNA)のインピーダンスマッチング(その7・LNAの設計(後編))
- 【第31話】 低雑音増幅器(LNA)のインピーダンスマッチング(その6・LNAの設計 (前編))
- 【第30話】 低雑音増幅器(LNA)のインピーダンスマッチング(その5・定NF円)
- 【第29話】 低雑音増幅器(LNA)のインピーダンスマッチング(その4・ノイズパラメータ)
- 【第28話】 低雑音増幅器(LNA)のインピーダンスマッチング(その3・NFマッチ)
- 【第27話】 低雑音増幅器(LNA)のインピーダンスマッチング(その2・NFとSN比)
- 【第26話】 低雑音増幅器(LNA)のインピーダンスマッチング(その1・雑音とは何か)
- 【第25話】 そのインピーダンス、本当に存在しますか? (その2)
- 【第24話】 そのインピーダンス、本当に存在しますか? (その1)
- 【第23話】 トランジスタの利得とミスマッチの関係
- 【第22話】 トランジスタの出力インピーダンスと負荷インピーダンス
- 【第21話】 S12と付き合う(その3)
- 【第20話】 S12と付き合う(その2)
- 【第19話】 S12と付き合う(その1)
- 【第18話】 S12の正体
- 【第17話】 増幅器とSパラメータ(その2)
- 【第16話】 増幅器とSパラメータ(その1)
- 【第15話】 Qとは何か(その3)
- 【第14話】 Qとは何か(その2)
- 【第13話】 Qとは何か(その1)
- 【第12話】 λ/4線路の共振と分布定数回路(その2)
- 【第11話】 λ/4線路の共振と分布定数回路(その1)
- 【第10話】 Sパラメータの基礎
- 【第9話】 直列共振と並列共振 その2
- 【第8話】 直列共振と並列共振
- 【第7話】 スミスチャートは日本人の発明?
- 【第6話】 スミスチャートとは何か(その2)
- 【第5話】 伝送線路と反射係数(その2)
- 【第4話】 伝送線路と反射係数
- 【第3話】 スミスチャートとは何か(その1)
- 【第2話】 インピーダンスマッチングの方法
- 【第1話】 なぜインピーダンスマッチング?
お知らせ
-
2022.11.15
11月号後半の記事をアップしました
-
2022.11.1
11月号の記事をアップしました
-
2022.10.17
10月号後半の記事をアップしました
-
2022.10.3
10月号の記事をアップしました
-
2022.9.15
9月号後半の記事をアップしました
-
2022.9.1
9月号の記事をアップしました
-
2022.8.15
8月号後半の記事をアップしました
-
2022.8.1
8月号の記事をアップしました
-
2022.7.15
7月号後半の記事をアップしました
-
2022.7.1
7月号の記事をアップしました
-
2022.6.15
6月号後半の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JL3ZGL」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2022.6.1
6月号の記事をアップしました
6月4日(土)、JH1CBX/3が14MHz SSBに初オンエアします。 入感がありましたらぜひお声がけください。 -
2022.5.16
5月号後半の記事をアップしました
-
2022.5.2
5月号の記事をアップしました
5月14日(土)、JL3ZGLはオペレーターにMasacoさんを迎えHAMtte交信パーティに 参加します。詳しくは4月号のニュースをご確認ください。 -
2022.4.15
4月号後半の記事をアップしました
-
2022.4.1
4月号の記事をアップしました
-
2022.3.15
3月号後半の記事をアップしました
-
2022.3.1
3月号の記事をアップしました
-
2022.2.15
2月号後半の記事をアップしました
-
2022.2.1
2月号の記事をアップしました
-
2022.1.17
1月号後半の記事をアップしました
-
2022.1.5
1月号の記事をアップしました
トップページに表示する表紙写真を募集中です。横1000x縦540ピクセルのサイズでご自慢の写真をメール添付でご送付ください。(infoアットマークfbnews.jp) 採用者には、月刊FB NEWSロゴ入りマグネットバーを送らせていただきます。 なお「撮影者: JA3YUA」の様に表記させていただきますが、表記不要の方は、その旨合わせてご連絡ください。 -
2021.12.15
12月号後半の記事をアップしました
-
2021.12.1
12月号の記事をアップしました
-
2021.11.15
11月号後半の記事をアップしました
-
2021.11.01
2021年11月号の記事をアップしました
-
2021.10.15
10月号後半の記事をアップしました
-
2021.10.01
2021年10月号の記事をアップしました
-
2021.09.15
9月号後半の記事をアップしました
-
2021.09.01
2021年9月号の記事をアップしました
-
2021.08.16
8月号後半の記事をアップしました
-
2021.08.02
2021年8月号の記事をアップしました
-
2021.07.15
7月号後半の記事をアップしました
-
2021.07.01
2021年7月号の記事をアップしました
-
2021.06.15
6月号後半の記事をアップしました
-
2021.06.01
2021年6月号の記事をアップしました
-
2021.05.17
5月号後半の記事をアップしました
-
2021.05.06
2021年5月号の記事をアップしました
-
2021.04.15
4月号後半の記事をアップしました
-
2021.04.01
2021年4月号の記事をアップしました
連載記事 Masacoの「むせんのせかい」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.15
3月号後半の記事をアップしました
連載記事「今月のハム」はコロナ禍の影響により、取材ができない状況が続いており、状況が改善されるまで不定期掲載とさせていただきます。よろしくお願いいたします。 -
2021.03.01
2021年3月号の記事をアップしました
-
2021.02.15
2月号後半の記事をアップしました
-
2021.02.01
2021年2月号の記事をアップしました
-
2021.01.15
1月号後半の記事をアップしました
-
2021.01.05
2021年1月号の記事をアップしました
-
2020.12.15
12月号後半の記事をアップしました
-
2020.12.01
2020年12月号の記事をアップしました
-
2020.11.16
11月号後半の記事をアップしました
-
2020.11.02
2020年11月号の記事をアップしました
-
2020.10.15
10月号後半の記事をアップしました
-
2020.10.01
2020年10月号の記事をアップしました
-
2020.09.15
9月号後半の記事をアップしました
-
2020.09.01
2020年9月号の記事をアップしました
-
2020.08.17
8月号後半の記事をアップしました
-
2020.08.03
2020年8月号の記事をアップしました
-
2020.07.15
7月号後半の記事をアップしました
-
2020.07.01
2020年7月号の記事をアップしました
-
2020.06.15
6月号後半の記事をアップしました
-
2020.06.01
2020年6月号の記事をアップしました
-
2020.05.01
2020年5月号の記事をアップしました
-
2020.04.15
4月号後半の記事をアップしました
-
2020.04.01
2020年4月号の記事をアップしました
-
2020.03.16
3月号後半の記事をアップしました
-
2020.03.09
JARD、eラーニングでのアマチュア無線国家資格取得を呼び掛けるお知らせを、臨時休校で自宅待機中の小中高生に向けて発表。詳しくはこちら。
-
2020.03.02
2020年3月号の記事をアップしました
-
2020.02.17
2月号後半の記事をアップしました
-
2020.02.03
2020年2月号の記事をアップしました
-
2020.01.15
1月号後半の記事をアップしました
-
2020.01.06
2020年1月号の記事をアップしました
-
2019.12.16
12月号後半の記事をアップしました
-
2019.12.02
2019年12月号の記事をアップしました
-
2019.11.15
11月号後半の記事をアップしました
-
2019.11.01
2019年11月号の記事をアップしました
-
2019.10.15
10月号後半の記事をアップしました
-
2019.10.01
2019年10月号の記事をアップしました
-
2019.09.17
9月号後半の記事をアップしました
-
2019.09.02
2019年9月号の記事をアップしました
-
2019.08.16
8月号後半の記事をアップしました
-
2019.08.01
2019年8月号の記事をアップしました
-
2019.07.16
7月号後半の記事をアップしました
-
2019.07.01
2019年7月号の記事をアップしました
-
2019.06.17
6月号後半の記事をアップしました
-
2019.06.01
2019年6月号の記事をアップしました
-
2019.05.20
5月号後半の記事をアップしました
-
2019.05.07
2019年5月号の記事をアップしました
-
2019.04.15
4月号後半の記事をアップしました
-
2019.04.01
2019年4月号の記事をアップしました
-
2019.03.15
3月号後半の記事をアップしました
-
2019.03.01
2019年3月号の記事をアップしました
-
2019.02.15
2月号後半の記事をアップしました
-
2019.02.01
2019年2月号の記事をアップしました
-
2019.01.18
1月号後半の記事をアップしました
-
2019.01.07
2019年1月号の記事をアップしました
-
2018.12.17
12月号後半の記事をアップしました
-
2018.12.01
2018年12月号の記事をアップしました
-
2018.11.15
11月号後半の記事をアップしました
-
2018.11.01
2018年11月号の記事をアップしました
-
2018.10.15
10月号後半の記事をアップしました
-
2018.10.01
2018年10月号の記事をアップしました
-
2018.09.15
9月号後半の記事をアップしました
-
2018.09.01
2018年9月号の記事をアップしました
-
2018.08.17
8月号後半の記事をアップしました
-
2018.08.01
2018年8月号の記事をアップしました
-
2018.07.17
7月号後半の記事をアップしました
-
2018.07.02
2018年7月号の記事をアップしました
-
2018.06.15
6月号後半の記事をアップしました
-
2018.06.01
2018年6月号の記事をアップしました
-
2018.05.15
5月号後半の記事をアップしました
-
2018.05.01
2018年5月号の記事をアップしました
-
2018.04.16
4月号後半の記事をアップしました
-
2018.04.02
2018年4月号の記事をアップしました
-
2018.03.15
3月号後半の記事をアップしました
-
2018.03.01
2018年3月号の記事をアップしました
-
2018.02.15
2月号後半の記事をアップしました
-
2018.02.01
2018年2月号の記事をアップしました
-
2018.01.15
1月号後半の記事をアップしました
-
2018.01.05
2018年1月号の記事をアップしました
-
2017.12.15
12月号後半の記事をアップしました
-
2017.12.1
12月号をアップしました
-
2017.11.15
11月号後半の記事をアップしました
-
2017.11.1
11月号をアップしました
-
2017.10.16
10月号後半の記事をアップしました
-
2017.10.2
10月号をアップしました
-
2017.9.15
What a healthy time! ~健康を応援する特別なお料理~/第3回 食物繊維たっぷり! 海藻の和風リゾット、FB Monthly Fashion/第9回 秋っぽい柄&色コーデ、子供の無線教室/第9回 「アンテナの形や大きさに注目!!」を掲載しました
-
2017.9.4
<速報>ハムフェア2017を掲載しました
-
2017.9.1
9月号をアップしました
-
2017.8.17
What a healthy time! ~健康を応援する特別なお料理~/第2回 和風のポトフ 納豆ソース添え、FB Monthly Fashion/第8回 夏のお出かけコーデ、子供の無線教室/第8回 「無線機にはどんなものがあるの?」を掲載しました
-
2017.8.1
8月号をアップしました
-
2017.7.18
What a healthy time! ~健康を応援する特別なお料理~/第1回 メロンの冷製スープ ナッツのアイスクリームのせ、FB Monthly Fashion/第7回 コットンTシャツコーデとボーイズコーデ、子供の無線教室/第7回 「電波はどうやって海外や宇宙に届くの?」を掲載しました
-
2017.7.1
7月号をアップしました
-
2017.6.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第9回 FB Girlsの野望 with ムースと甘エビのタルタル、FB Monthly Fashion/第6回 雨の日コーデと親子コーデ、子供の無線教室/第6回 「電波はいろいろなところで大活躍!!」を掲載しました
-
2017.6.1
6月号をアップしました
-
2017.5.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第8回 番外編 春うらら♪豪華弁当でお花見、FB Monthly Fashion/第5回 ブラウス&シャツを使ったコーディネート、子供の無線教室/第5回 「周波数によって変わる、電波の特徴」を掲載しました
-
2017.5.1
5月号をアップしました
-
2017.4.17
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第7回 ARDFの思い出 with 2種類のソースのカルボナーラ、FB Monthly Fashion/第4回 Gジャンを使ったコーディネート、子供の無線教室/第4回 「電波の性質を覚えよう」を掲載しました
-
2017.4.1
4月号をアップしました
-
2017.3.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第6回 初めてのQSOの思い出 with グリーンのアクアパッツァ、FB Monthly Fashion/第3回 ピンクを使ったコーディネート、子供の無線教室/第3回 「電波はどうやって伝わるの?」を掲載しました
-
2017.3.1
3月号をアップしました
-
2017.2.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第5回 FB Girlsの試験の思い出 withウマ辛和風スープ、FB Monthly Fashion/第2回 デニムと明るめニットのコーディネートを掲載しました
-
2017.2.1
2月号をアップしました
-
2017.1.16
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第4回 YLハムを増やす秘策とは?! withおなかにやさしいお料理、【新連載】FB Monthly Fashion/第1回 アウター別おすすめコーディネート(ライダース・ノーカラー・ダッフル)を掲載しました
-
2017.1.5
1月号をアップしました
-
2016.12.15
What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第3回 YLハムの行く年来る年 with ブイヤベースの洋風お鍋を掲載しました
-
2016.12.1
12月号をアップしました
-
2016.11.15
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(後編)!、What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第2回 YLハムの悩み解決!with サケのフレンチトーストを掲載しました
-
2016.11.1
11月号をアップしました
-
2016.10.17
FB Girlsが行く!!~元気娘がアマチュア無線を体験~/<第3話>元気娘、秋の休日を楽しむ!!(前編)!、【新連載】What a tasty time! ~グルメYLたちのGirl'sトーク♥~/第1回 FB GirlsのプライベートQSO with 土瓶蒸しのリゾットを掲載しました
外部リンク
アマチュア無線関連機関/団体
各総合通信局/総合通信事務所
アマチュア無線機器メーカー(JAIA会員)
次号は 12月 1日(木) に公開予定